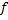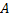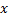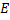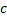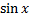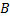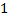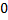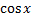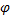Множество действительных чисел несчетные.


| |
| |
 Рассмотрим отрезок из действительных чисел
Рассмотрим отрезок из действительных чисел В этом множестве любое число записывается десятичной дробью, в которой после нуля следует любая бесконечная последовательность цифр от 0 до 9, за исключение последовательностей, начиная с нечетного элемента (0,99999…9=1)
|
| 0,000…0… | |
| 0,010…0… | |
| 0,1111…0… | |
| 0,12345… | |
| 0,121241…. | |
| … | … |
0,12267 – данная последовательность не совпадает ни с одной из последовательностей, вписанных в столбец, поскольку в i-ой последовательности она отличается в i-ом знаке и поэтому не будет пронумерована.
И значит, множество действительных чисел неравномощно счетному множеству.
Вопрос 27. Функция, последовательность, их пределы (примеры бесконечно малых и больших последовательностей).
|
|









































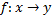
 Функция переводящая в натуральный ряд в множество У называется последовательностью.
Функция переводящая в натуральный ряд в множество У называется последовательностью.






| |
| |
| |
| |




 Последовательность принято обозначать символом
Последовательность принято обозначать символом 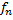 , при этом
, при этом  ее можно задавать двумя способами: словесно и с помощью
ее можно задавать двумя способами: словесно и с помощью
графика.
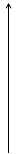 |
 Предел функции:
Предел функции:
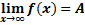

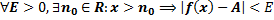
 Пример:
Пример: 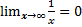 – гипербол
– гипербол
|


|
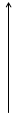 Функция sinxне имеет предела
Функция sinxне имеет предела 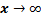
|





|

|
| |
 Функция имеет предел в точке
Функция имеет предел в точке 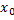
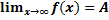 тогда и только тогда, когда:
тогда и только тогда, когда: для 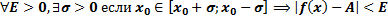
Предел последовательности:пределом последовательности 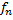 называется число А и символ
называется число А и символ 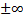 , тогда и только тогда, когда:
, тогда и только тогда, когда:
1) предел 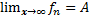 тогда и только тогда, когда для
тогда и только тогда, когда для 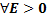 ,
, 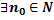 ,что из
,что из 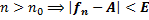 ;
; 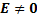
2) 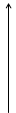 предел
предел 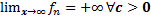 ,
, 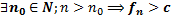
|








Последовательность 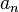 называется бесконечно малой, если
называется бесконечно малой, если 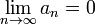 . Например, последовательность чисел
. Например, последовательность чисел 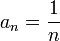 — бесконечно малая
— бесконечно малая
Функция называется бесконечно малой в окрестности точки 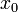 , если
, если 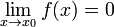
Последовательность 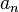 называется бесконечно большой, если
называется бесконечно большой, если 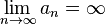
Функция называется бесконечно большой в окрестности точки 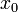 , если
, если 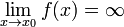
Вопрос 28. Теорема о пределе монотонной ограниченной последовательности, теорема о пределе промежуточной функции.
Предел монотонной ограниченной последовательности:
Если 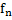 не убывающая последовательность ограниченная сверху, то она имеет предел который совпадает сее супремомом(sup):
не убывающая последовательность ограниченная сверху, то она имеет предел который совпадает сее супремомом(sup):
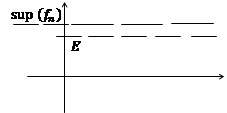
Доказательство: рассмотрим любое сколь угодно малое Е>0,если 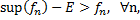 то получим противоречие, поскольку найдется значение
то получим противоречие, поскольку найдется значение 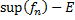 меньше наименьшей верхней грани последовательности
меньше наименьшей верхней грани последовательности 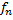 следовательно, существует такое
следовательно, существует такое 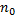 для которого
для которого 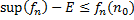
Но тогда поскольку последовательность не убывающая и для всех 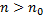 верно
верно 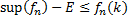
Аналогично, можно доказать что любая невозрастающая ограниченная снизу последовательность имеет предел ее инфиниму.
Теорема о пределе промежуточной функции:

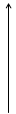 Если
Если 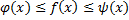 для
для 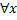 и
и 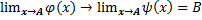
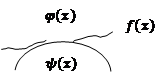 |

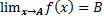
Доказательство: вычтем из двойного неравенства В: 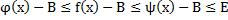 , это означает что
, это означает что
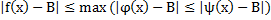 . Следовательно для любого Е,
. Следовательно для любого Е, 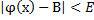 - для некоторого
- для некоторого 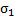 и
и 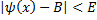 - для некоторого
- для некоторого 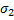 , то
, то 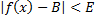 , для min(
, для min( 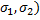 .
.
Теорема для промежуточной функции также справедлива, когда А, символ 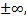 и также в случае
и также в случае 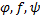 –последовательности.
–последовательности.
Воспрос 29. Свойства пределов: сумма, произведение, частное пределов.
Сумма:
Пусть 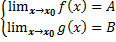 Тогда
Тогда 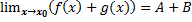
Доказательство:
Из леммы следует (функция f(x) имеет в точке 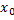 предел, равный А тогда и только тогда, когда да и только тогда, когда
предел, равный А тогда и только тогда, когда да и только тогда, когда 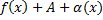 , где
, где 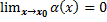 ):
):
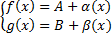
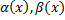 –бесконечно малые в точке
–бесконечно малые в точке 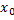
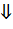
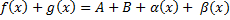 -есть сумма постоянных значений и бесконечно малых, следовательно, по лемме это утверждение верно.
-есть сумма постоянных значений и бесконечно малых, следовательно, по лемме это утверждение верно. 
Произведение:
Найдем предел произведения 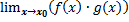
|

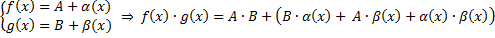
Следовательно, 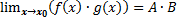 - по лемме.
- по лемме. 
Частное:
Найдем предел частного 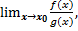 где
где 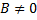
Докажем, что 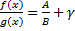 , где
, где 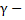 бесконечно малая величина в точке
бесконечно малая величина в точке 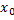
Найдем 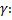
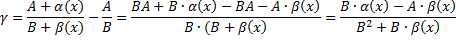
Это величина является бесконечно малой, поскольку числитель – бесконечно малая величина, а знаменатель – ограниченная функция, 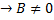 Следовательно,
Следовательно, 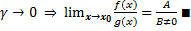
Воспрос 30. Первый замечательный предел.
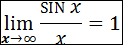
Доказательство:
|

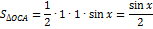
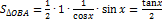
|
|



|
|
|
|
|

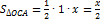 (площадь сегмента)
(площадь сегмента)
|

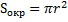

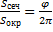
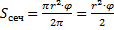
Значит 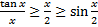 (следовательно,
(следовательно, 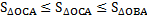 ) – умножим на 2 и разделим на sinx:
) – умножим на 2 и разделим на sinx:
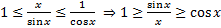 заметим, что при
заметим, что при 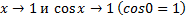 поэтому
поэтому 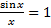 по теореме о промежуточной функции (Если
по теореме о промежуточной функции (Если 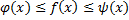 для
для 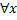 и
и 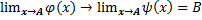 , то
, то 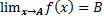 ).
).
Воспрос 31. Второй замечательный предел.
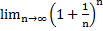 , где
, где 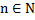 (для последовательностей)
(для последовательностей)
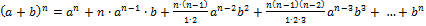 –Бином Ньютона.
–Бином Ньютона.
Используя Бином Ньютонапреобразуем 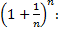




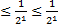
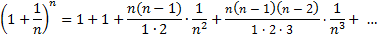
Докажем, что последовательность 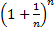 ограничена сверху. Для этого заметим, что в каждом из слагаемых, начиная с третьего выполняется:
ограничена сверху. Для этого заметим, что в каждом из слагаемых, начиная с третьего выполняется:
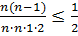
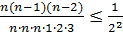
Следовательно, вся сумма 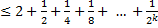 и следовательно, последовательность
и следовательно, последовательность 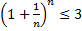
Докажем, что последовательность возрастает. Для этого заметим, что с увеличением nрастет количество слагаемых в сумме и каждое слагаемое увеличивается. По этой причине последовательность возрастает.
По доказанной теореме об ограниченной возрастающей последовательности у последовательности 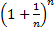
есть предел. И этот предел называют числом e.
Вопрос 32.Неопределенности.Сравнение бесконечно малых. Таблица эквивалентности.
Неопределенности могут быть :
1)  Т.е. рассматриваемая функция является отношением двух функций, причем в точке x0 и числитель, и знаменатель равны 0.
Т.е. рассматриваемая функция является отношением двух функций, причем в точке x0 и числитель, и знаменатель равны 0.
2)  Т.е. рассматриваемая функция является отношением двух функций, причем в точке x0 и числитель, и знаменатель равны ¥.
Т.е. рассматриваемая функция является отношением двух функций, причем в точке x0 и числитель, и знаменатель равны ¥.
3) 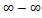 Т.е. рассматриваемая функция является разностью двух функций, и в точке x0 обе эти функции становятся бесконечно большими.
Т.е. рассматриваемая функция является разностью двух функций, и в точке x0 обе эти функции становятся бесконечно большими.
4) 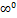 5)
5) 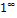 6)
6) 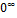
!!!НУЖНЫ ПРИМЕРЫ!!!