Понятие обратной матрицы существует только для квадратных матриц.

В том случае, если определитель матрицы равен НУЛЮ – обратной матрицы НЕ СУЩЕСТВУЕТ.

Минор – это определитель, составленный из первоночального определителя, путем вычеркивания k-строк и k- любых столбцов.

Алгебраическим дополнением А_ij элемента а_ij матрицы n-го порядка называется его минор, взятый со знаком, зависящий от номера строки и номера столбца:

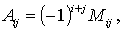
ДОК-ВО МЕТОД ПРИСОЕДИНЕЕНОЙ И ЭЛЕМЕНТАРНЫМИ ПРЕОБРАЗОВАНИЯМИ.

Вопрос 5. Теорема о Ранге матрице.

Рангом матрицы называется максимальная размерность его не нулевого минора.

Теорема. Ранг матрицы совпадает смаксимальной количеством её линейных независимых строк (столбцов).

Базисным минором матрицы называется любой ее ненулевой минор, порядок которого равен рангу матрицы.

Строки (столбцы) матрицы называются линейно зависимыми, если существует их линейная комбинация, не все коэффициенты в которой равны 0, равная нулевой строке (столбцу).

В противном случае строки (столбцы) называются линейно независимыми.

Доказательство (для строк).

1. Если бы базисные строки были линейно зависимыми, то с помощью эквивалентных преобразований из них можно было бы получить нулевую строку, что противоречит условию, что базисный минор не равен 0.

2. Строка, входящая в базисный минор, является линейной комбинацией его строк, в которой коэффициент при данной строке равен 1, а остальные коэффициенты равны 0.

Докажем это свойство для строки, не входящей в базисный минор.

Добавим к базисному минору эту строку (пусть ее номер – k) и любой столбец матрицы (пусть его номер – j). Затем разложим полученный определитель, равный 0 (так как его порядок больше ранга матрицы) по j-му столбцу:

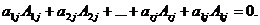Поскольку 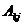является базисным минором, 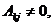поэтому, разделив полученное равенство на 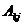, найдем, что 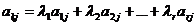для всех j=1,2,…,n, где 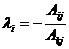. Следовательно, выбранная строка является линейной комбинацией базисных строк. Теорема доказана

Вопрос 6. Теорема Кронекера-Капелли

Пусть имеется система линейных уравнений

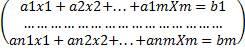(x1 – где 1 это индекс,который находится внизу)

А=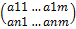

A_{расширенная}=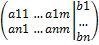

Теорема.

Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы.

Доказательство.

Пусть система совместна. Тогда существуют числа 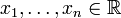такие, что 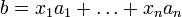. Следовательно, столбец 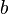является линейной комбинацией столбцов 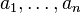матрицы 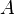. Из того, что ранг матрицы не изменится, если из системы его строк (столбцов) вычеркнуть или приписать строку (столбец), которая является линейной комбинацией других строк (столбцов) следует, что .

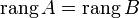Достаточность

Пусть 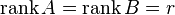. Возьмем в матрице 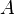какой-нибудь базисный минор. Так как 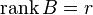, то он же и будет базисным минором и матрицы 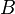. Тогда, согласно теореме о базисном миноре, последний столбец матрицы 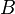будет линейной комбинацией базисных столбцов, то есть столбцов матрицы 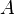. Следовательно, столбец свободных членов системы является линейной комбинацией столбцов матрицы .

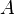Теорема о базисном миноре.

Теорема.В произвольной матрице А каждый столбец (строка) является линейной комбинацией столбцов (строк), в которых расположен базисный минор.

Таким образом, ранг произвольной матрицы А равен максимальному числу линейно независимых строк (столбцов) в матрице.