Вопрос1.понятие первообразной функции. неопределенный интеграл. свойства неопределенного интеграла.
ВОПРОС 13. ДИФФЕРЕНЦИРУЕМОСТЬ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ
Функция u=f(x1, ..., xm) называется дифференцируемой в точке
M(x1, ..., xm), если ее полное приращение в этой точке может быть представлено в виде
f(x1+∆x1, ..., xm+∆xm) – f(x1, ..., xm) ≡
≡ ∆u = A1∆x1 + A2∆x2 + ... + Am∆xm + α1∆x1 + ... + αm∆xm
где А1, А2, ..., Аm – некоторое, не зависящие от ∆x1, ..., ∆xm, числа,
а α1, α2, ..., αm – бесконечно малые при ∆x1→0, ..., ∆xm→0 функции, равные 0 при
∆x1=∆x2=... =∆xm=0.
Если положить ρ = + + ∆ ∆ x x
1 m
2 2
. . . , то условие дифференцируемости может быть
записано в виде:
∆u = A1∆x1 + A2∆x2 + ... + Am∆xm + )(ρ) (1)
Оба представления эквивалентны и означают, что приращение функции предста-
вимо в виде линейной части (по ∆x1, ..., ∆xm) и членов более высокого порядка (по ∆x1, ...,
∆xm или ρ).
Теорема 1. Если функция u=f(x1, ..., xm) дифференцируема в точке
M(x1, ..., xm), то в этой точке существуют частные производные по всем аргумен-
там, причем ∂u\∂xi=Ai, где Аi определяются из условия дифференцируемости.
ВОПРОС 14. КАСАТЕЛЬНАЯ ПЛОСКОСТЬ.
КАСАТЕЛЬНАЯ ПЛОСКОСТЬ
к поверхности S в точке М- плоскость, проходящая через точку Мп характеризующаяся тем свойством, что расстояние от этой плоскости до переменной точки М' поверхности Sпри произвольном стремлении М' к Мявляется бесконечно малым по сравнению с расстоянием ММ'. Если поверхность Sзадана уравнением z=f(x, у), то уравнение К. п. в точке ( х 0, у 0,z0), где zo=f'(zo, y0), имеет вид: 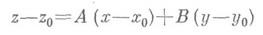
в том и только том случае, когда функция f(x, у )имеет в точке ( х 0, у 0 )полный дифференциал. В этом случае Аи Bсуть значения частных производных df/dx и df/dy в точке (x0,у 0).
ВОПРОС 17. ЛОКАЛЬНЫЙ ЭКСТРЕМУМ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ, НЕОБХОДИМЫЕ, ДОСТАТОЧНЫЕ УСЛОВИЯ ЕГО СУЩЕСТВОВАНИЯ.
Локальный это тоже самое что и наименьшее и наибольшее значении функции.
Наибольшее или наименьшее знчение функции может достигаться как в точках экстремума, так и в точках на концах отрезка.
Для нахождения наибольшего и наименьшего значений на отрезке рекомендуется пользоваться следующей схемой:
1) Найти производную функции
2) Найти критические точки функции, в которых производная равна нулю или не существует.
3) Найти значения функции в критических точках и на конфах отрезкаи выбрать из них наибольшее и наименьшее.
БИЛЕТ 21. ПРИЗНАКИ СХОДИМОСТИ ЧИСЛОВЫХ РЯДОВ С ПОЛОЖИТЕЛЬНЫМИ ЧЛЕНАМИ
Пусть ряд ∑An = a1+a2+…+An+… будет положительным , т.е. an>0 (n=1,2,3,...)
Тогда очевидно, An+1=An+an+1>An, т.е. Аn оказывается возрастающей. На основании
теоремы о пределе монотонной последовательности, мы непосредственно приходит к сле-
дующему основному в теории положительных рядов предложению!
Положительный ряд всегда имеет сумму; эта сумма будет конечной (и, следова-
тельно, ряд – сходящимся), если частичные суммы ряда ограничены сверху, и бесконеч-
ной (а ряд – расходящимся) в противном случае.
БИЛЕТ 23. АБСОЛЮТНАЯ И УСЛОВНАЯ СХОДИМОСТИ ЧИСЛОВОГО РЯДА.
Рассмотрим произвольный знакопеременный ряд
U1 + U2 + ... + Un + ... , (8.1)
т. е. ряд с членами произвольных знаков. Рассмотрим ряд, составленный из абсолютных
величин членов ряда (8.1):
|U1| + |U2| + ... + |Un| + ... . (8.2)
Теорема.
Если сходится ряд (8.2), то сходится и ряд (8.1).
Если ряд (8.1) сходится вместе с рядом (8.2), составленным из абсолютных величин
его членов, то про ряд (8.1) говорят, что он абсолютно сходится.
Если ряд (8.1) сходится и ряд (8.2) расходится, то ряд (8.1) называют условно сходящимся.
Между свойствами абсолютно и условно сходящихся рядов имеется глубокое различие.
Теорема.
Если ряд сходится абсолютно, то он остается абсолютно сходящимся при любой
перестановке его членов, причем сумма ряда не зависит от порядка его членов.
Если ряд сходится условно, то какое бы мы ни задали число А, или символ + ∞ или
– ∞, можно так переставить члены этого ряда, чтобы его сумма оказалась в точности рав-
ной А (или + ∞ или – ∞). Более того, можно так переставить члены условно сходящегося
ряда, что ряд, полученный после перестановки членов, окажется расходящимся.
Определение : ряд называется абсолютно сходящимся , если сходится как сам ряд , так и ряд, составленный из абсолютных величин его членов.
Определение: Ряд называется условно сходящимся, если сам ряд сходится, а ряд, составленный из абсолютных величин его членов, расходится.
Следствие.
Если степенной ряд расходится при некотором значении х = х1, то он расходится и
при всех значениях |x|>|x1|.
Любой степенной ряд сходится при значении х=0. Есть степенные ряды, которые
сходятся только при х=0 и расходятся при остальных значениях х.
Область сходимости может состоять из всех точек оси Ох, другими словами, ряд
может сходится при всех х.
Из теоремы Абеля и ее следствия получаем, что все точки сходимости расположе-
ны от начала координат не дальше, чем любая из точек расходимости. Совершенно ясно,
что точки сходимости будут целиком заполнять некоторый интервал с центром в начале
координат.
Таким образом, можно сказать, что для каждого степенного ряда, имеющего как
точки сходимости, так и точки расходимости, существует такое положительное число R,
что для всех х, по модулю меньших R (|x|<R), ряд абсолютно сходится, а для всех х, по
модулю больших R (|x|>R), ряд расходится.
ВОПРОС1.ПОНЯТИЕ ПЕРВООБРАЗНОЙ ФУНКЦИИ. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ. СВОЙСТВА НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА.
1.Функция Ф(х) называется первообразной для функции ф(х) на промежутке Х, если в каждой точке х этого промежутка справедливо равентсво Ф’(x)=f(x).
2.Совокупность всех первообразных для функции ф(х) на промежутке Х называется неопределенным интегралом от функции ф(х) и обозначается ∫f(x)dx = F(x)+C, где С – произвольная постоянная.
В записи ∫f(x)dx f(x) подыинтегральной функцией, а f(x)dx – подынтегральным выражением. Нахождение неопределенного интеграла от некоторой функции называется интегрированием этой функции. Операции интегрир. И дифференцирования взаимно обратны.
3.Основные свойства неопределенного интеграла:
1. (∫f(x)dx)’ = f(x)
2. d(∫f(x)dx) = f(x)dx
3. ∫dF(x) = F(x)+C
4. ∫αf(x)dx = α∫f(x)dx ,где альфа некоторое число
5. ∫(f(x)±g(x))dx = ∫f(x)dx±∫g(x)dx.
ВОПРОС 2.ПРОСТЕЙШИЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ.
1.Метод замены переменной.
Одним из основных методов интегрирования является метод замены переменной( или метод подстановки), описываемый след формулой:
∫f(x)dx=∫f(φ(t)φ’(t)dt,
Где х = - функция, дифференцируемая на рассматриваемом промежутке.
Формула показывает, что переходя к новой переменной, достаточно выполнить замену переменной в подынтегральном выражении. По опр. Дифференциала подынтеграл. Выражения левой и правой частей равенства совпадают. Удачная замена переменной позволяет упростить исходный интеграл даже до табличных.
2.Метод интегрирования по частям.
Пусть u=u(x) , v=v(x) – дифференцируемые функции. По свойству дифференциала
D(uv)=vdu + udvИлиUdv=d(uv) _ vdu
Интегрируя левую и правую части последнего равенства и учитывая , получаем
∫udv = uv - ∫vdu
Формула называется формулой интегрирования по частям для неопределенного интеграла. При ее применении фиксируется разбиение подинтеграл. Выражения искомого интеграла на два сомножителя( и и дв). При переходе к правой части первый из них дифференцируется , второй интегрируется.
ВОПРОС 3. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ДРОБЕЙ.
Рациональной дробью называется отношение двух многочленов.
Рациональной дробью называется выражение вида 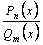 , где
, где 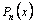 ,
, 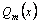 –многочлены степеней n и m соответственно.
–многочлены степеней n и m соответственно.
Если 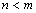 , рациональная дробь называется правильной, в противном случае
, рациональная дробь называется правильной, в противном случае 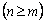 –неправильной.
–неправильной.
Если дробь неправильная, из нее можно выделить целую часть, разделив числитель на знаменатель.
Любую неправильную дробь можно представить в виде: 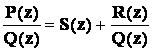 ,
,
где
P(z) = Q(z) S(z) + R(z),
a R(z) – многочлен, степень которого меньше степени Q(z).
Таким образом, интегрирование рациональных дробей сводится к интегрированию многочленов, то есть степенных функций, и правильных дробей, так как 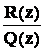 является правильной дробью.
является правильной дробью.
Простейшими (или элементарными) дробями называются дроби следующих видов:
1) 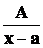 , 2)
, 2) 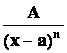 , 3)
, 3) 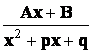 , 4)
, 4) 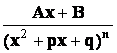
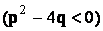 .
.
Каким образом они интегрируются:
1) 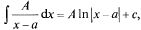
2) 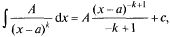
3) 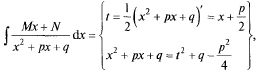
4) 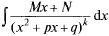 Пусть
Пусть 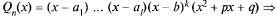 правильная :
правильная : 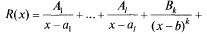
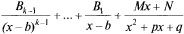
Всякую правильную дробь можно представить в виде суммы простейших дробей (без доказательства).
Следствие 1. Если 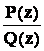 - правильная рациональная дробь, и если среди корней многочлена
- правильная рациональная дробь, и если среди корней многочлена 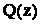 будут только простые действительные корни, то в разложении дроби на сумму простейших дробей будет присутствовать лишь простейшие дроби 1-го типа:
будут только простые действительные корни, то в разложении дроби на сумму простейших дробей будет присутствовать лишь простейшие дроби 1-го типа:
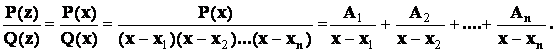
Пример 1. 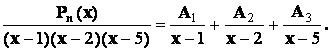
Следствие 2. Если 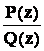 - правильная рациональная дробь, и если среди корней многочлена
- правильная рациональная дробь, и если среди корней многочлена 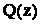 будут только кратные действительные корни, то в разложении дроби на сумму простейших дробей будет присутствовать лишь простейшие дроби 1-го и 2-го типов:
будут только кратные действительные корни, то в разложении дроби на сумму простейших дробей будет присутствовать лишь простейшие дроби 1-го и 2-го типов:
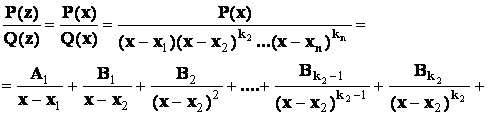
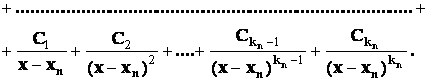
Пример2. 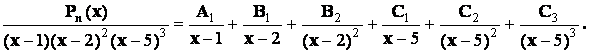
Следствие 3. Если 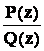 - правильная рациональная дробь, и если среди корней многочлена
- правильная рациональная дробь, и если среди корней многочлена 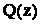 будут только простые комплексно - сопряженные корни, то в разложении дроби на сумму простейших дробей будет присутствовать лишь простейшие дроби 3-го типа:
будут только простые комплексно - сопряженные корни, то в разложении дроби на сумму простейших дробей будет присутствовать лишь простейшие дроби 3-го типа:
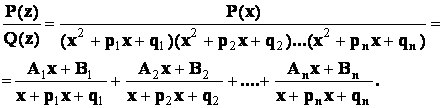
Пример 3. 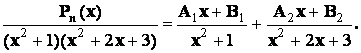
Следствие 4. Если 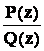 - правильная рациональная дробь, и если среди корней многочлена
- правильная рациональная дробь, и если среди корней многочлена 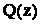 будут только кратные комплексно - сопряженные корни, то в разложении дроби на сумму простейших дробей будет присутствовать лишь простейшие дроби 3-го и 4-го типов:
будут только кратные комплексно - сопряженные корни, то в разложении дроби на сумму простейших дробей будет присутствовать лишь простейшие дроби 3-го и 4-го типов:
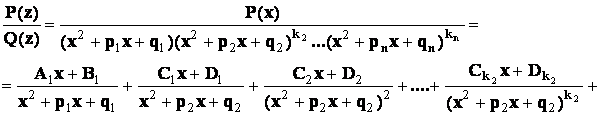
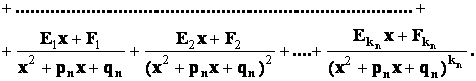
Пример 4.
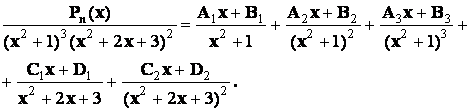
Для определения неизвестных коэффициентов в приведенных разложениях поступают следующим образом. Левую и правую часть разложения 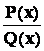 , содержащего неизвестные коэффициенты, умножают на
, содержащего неизвестные коэффициенты, умножают на 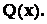 Получается равенство двух многочленов. Из него получают уравнения на искомые коэффициенты, используя, что:
Получается равенство двух многочленов. Из него получают уравнения на искомые коэффициенты, используя, что:
1. равенство справедливо при любых значениях Х (метод частных значений). В этом случае получается сколько угодно уравнений, любые m из которых позволяют найти неизвестные коэффициенты.
2. совпадают коэффициенты при одинаковых степенях Х (метод неопределенных коэффициентов). В этом случае получается система m – уравнений с m – неизвестными, из которых находят неизвестные коэффициенты.
3. комбинированный метод.
