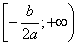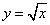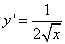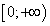Дифференцируемость и непрерывность.
Непрерывность функции есть необходимое условие ля ее дифференцируемости.
Функция y=f(x)называется дифференцируемой в некоторой точке x0, если она имеет в этой точке определенную производную, т.е. если предел отношения 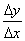 существует и конечен.
существует и конечен.
Если функция дифференцируема в каждой точке некоторого отрезка [а; b] или интервала (а; b), то говорят, что онадифференцируема на отрезке [а; b] или соответственно в интервале (а; b).
Справедлива следующая теорема, устанавливающая связь между дифференцируемыми и непрерывными функциями.
Теорема. Если функция y=f(x) дифференцируема в некоторой точке x0, то она в этой точке непрерывна.
Таким образом,из дифференцируемости функции следует ее непрерывность.
41.Основные правила дифференцирования
Пусть 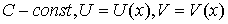 , тогда:
, тогда:
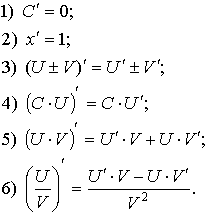
7) Если 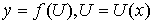 , то есть
, то есть 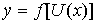 , где
, где 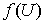 и
и 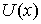 имеют производные, то
имеют производные, то 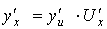 (правило дифференцирования сложной функции).
(правило дифференцирования сложной функции).
42. Производные функций: синуса, тангенса и обратных тригонометрических.
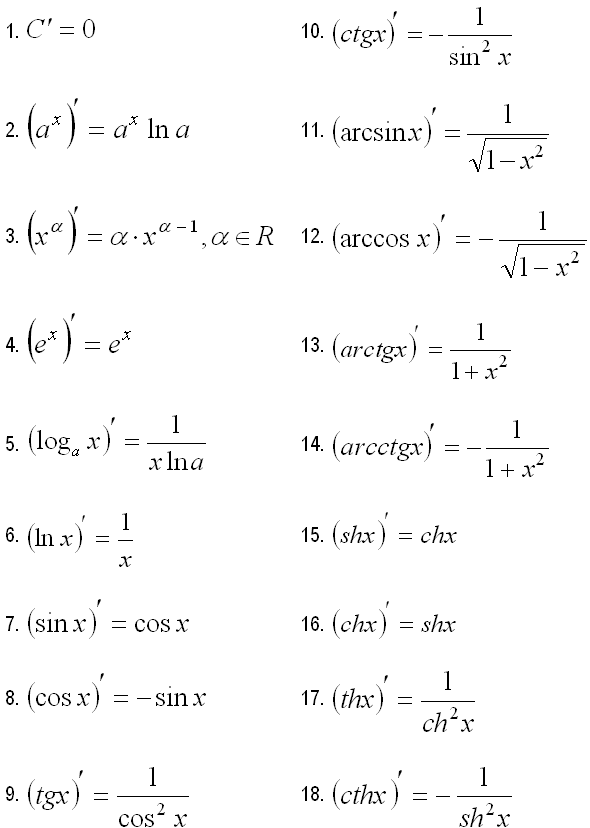
43. Производные функций: логарифм, показательная функция, стеленная.
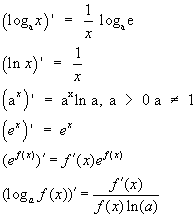

44. Логарифмическое дифференцирование, дифференцирование неявных функций.
| Логарифмическое дифференцирование | |||||||||||||||||||||||
Логарифмическим дифференцированием называется метод дифференцирования функций, при котором сначала находится логарифм функции, а затем вычисляется производная от него. Такой прием позволяет эффективно вычислять производные степенных и рациональных функций. Рассмотрим этот подход более детально. Пусть дана функция y = f(x). Возьмем натуральные логарифмы от обеих частей: 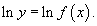 Теперь продифференцируем это выражение как сложную функцию, имея ввиду, что y - это функция от x. Теперь продифференцируем это выражение как сложную функцию, имея ввиду, что y - это функция от x. 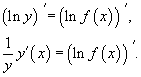 Отсюда видно, что искомая производная равна Отсюда видно, что искомая производная равна 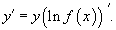 Неявно заданная функция:Если функция задана уравнением у=ƒ(х), разрешенным относительно у, то функция задана в явном виде (явная функция).Под неявным заданием функции понимают задание функции в виде уравнения F(x;y)=0, не разрешенного относительно у.Всякую явно заданную функцию у=ƒ (х) можно записать как неявно заданную уравнением ƒ(х)-у=0, но не наоборот.Не всегда легко, а иногда и невозможно разрешить уравнение относительно у (например, у+2х+cosy-1=0 или 2у-х+у=0).Если неявная функция задана уравнением F(x; у)=0, то для нахождения производной от у по х нет необходимости разрешать уравнение относительно у: достаточно продифференцировать это уравнение по x, рассматривая при этом у как функцию х, и полученное затем уравнение разрешить относительно у'.Производная неявной функции выражается через аргумент х и функцию у. 45 Дифференциал, его применение в приближенных вычислениях. Дифференциалом dy функции y=y(x) называется главная часть ее приращения, пропорциональная приращению Неявно заданная функция:Если функция задана уравнением у=ƒ(х), разрешенным относительно у, то функция задана в явном виде (явная функция).Под неявным заданием функции понимают задание функции в виде уравнения F(x;y)=0, не разрешенного относительно у.Всякую явно заданную функцию у=ƒ (х) можно записать как неявно заданную уравнением ƒ(х)-у=0, но не наоборот.Не всегда легко, а иногда и невозможно разрешить уравнение относительно у (например, у+2х+cosy-1=0 или 2у-х+у=0).Если неявная функция задана уравнением F(x; у)=0, то для нахождения производной от у по х нет необходимости разрешать уравнение относительно у: достаточно продифференцировать это уравнение по x, рассматривая при этом у как функцию х, и полученное затем уравнение разрешить относительно у'.Производная неявной функции выражается через аргумент х и функцию у. 45 Дифференциал, его применение в приближенных вычислениях. Дифференциалом dy функции y=y(x) называется главная часть ее приращения, пропорциональная приращению 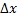 независимой переменно x. Дифференциал dx независимой переменной x равен ее приращению независимой переменно x. Дифференциал dx независимой переменной x равен ее приращению 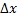 : : 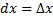 Дифференциал любой дифференцируемой функции y=y(x) равен произведению ее производной на дифференциал независмой переменной: Дифференциал любой дифференцируемой функции y=y(x) равен произведению ее производной на дифференциал независмой переменной: 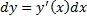 Если Если 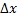 достаточно мало по абсолютной величине, то с точностью до бесконечно малых более высокого порядка, чем достаточно мало по абсолютной величине, то с точностью до бесконечно малых более высокого порядка, чем 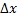 , имеет место приближенное равенство , имеет место приближенное равенство 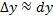 . Применение дифференциала в приближенных вычислениях. . Применение дифференциала в приближенных вычислениях. 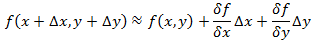 Теорема о производной сложной функции (дифференцирование сложной функции). Пусть x=x(t), y=y(t) – дифференцируемы в точке t, z=f(x,y) – дифференцируема в точке t(x,y), если t получит Δt, то x получит Δx, y – Δy, z –Δz, а т.к. функция z дифференцируема, то ее приращение Теорема о производной сложной функции (дифференцирование сложной функции). Пусть x=x(t), y=y(t) – дифференцируемы в точке t, z=f(x,y) – дифференцируема в точке t(x,y), если t получит Δt, то x получит Δx, y – Δy, z –Δz, а т.к. функция z дифференцируема, то ее приращение 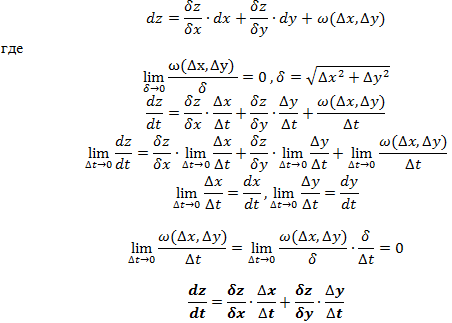 46. Геометрический смысл и свойства дифференциала Геометрический смысл:дифференциал функции f(x), соответствующей данным значениям x и Δx, равен приращению ординаты касательной к кривой y=f(x) в данной точке х. Дифференциал функции обладает свойствами: 1. Дифференциал постоянной равен нулю: dc = 0, с = const. 2. Дифференциал суммы дифференцируемых функцийравен сумме дифференциалов слагаемых: d(u+v)=du + dv Следствие. Если две дифференцируемые функции отличаются постоянным слагаемым, то их дифференциалы равны d(u+c) = du (c= const). 3. Дифференциал произведения двух дифференцируемых функций равен произведению первой функции на дифференциал второй плюс произведение второй на дифференциал первой: d(uv) = udv + vdu. Следствие. Постоянный множитель можно выносить за знак дифференциала d(cu) = cdu (с = const). 4. Дифференциал частного u/v двух дифференцируемых функций и = и(х) и v = v(x) определяется формулой 46. Геометрический смысл и свойства дифференциала Геометрический смысл:дифференциал функции f(x), соответствующей данным значениям x и Δx, равен приращению ординаты касательной к кривой y=f(x) в данной точке х. Дифференциал функции обладает свойствами: 1. Дифференциал постоянной равен нулю: dc = 0, с = const. 2. Дифференциал суммы дифференцируемых функцийравен сумме дифференциалов слагаемых: d(u+v)=du + dv Следствие. Если две дифференцируемые функции отличаются постоянным слагаемым, то их дифференциалы равны d(u+c) = du (c= const). 3. Дифференциал произведения двух дифференцируемых функций равен произведению первой функции на дифференциал второй плюс произведение второй на дифференциал первой: d(uv) = udv + vdu. Следствие. Постоянный множитель можно выносить за знак дифференциала d(cu) = cdu (с = const). 4. Дифференциал частного u/v двух дифференцируемых функций и = и(х) и v = v(x) определяется формулой 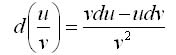 5. Свойство независимости вида дифференциала от выбора независимой переменной (инвариантность формы дифференциала): дифференциал функции равен произведению производной на дифференциал аргумента независимого от того, является ли этот аргумент независимой переменной или функцией другой независимой переменной. 47. Производные и дифференциалы высших порядков Пусть производная некоторой функции f дифференцируема. Тогда производная от производной этой функции называется второй производной функции fи обозначается f". Таким образом, f"(x) = (f'(x))'. Если дифференцируема (n - 1)-я производная функции f, то ее n-й производной называется производная от (n - 1)-й производной функции f и обозначается f(n). Итак, f(n)(x) = (f(n-1)(x))', n ϵ N, f(0)(x) = f(x). Число n называется порядком производной. Дифференциалом n-го порядка функции f называется дифференциал от дифференциала (n - 1)-го порядка этой же функции. Таким образом, dnf(x) = d(dn-1f(x)), d0f(x) = f(x), n ϵ N. Если x - независимая переменная, то dx = const и d2x = d3x = ... = dnx = 0. В этом случае справедлива формула dnf(x) = f(n)(x)(dx)n. 48. Функция, заданная параметрически Пусть зависимость между аргументом х и функцией у задана параметрически в виде двух уравнений 5. Свойство независимости вида дифференциала от выбора независимой переменной (инвариантность формы дифференциала): дифференциал функции равен произведению производной на дифференциал аргумента независимого от того, является ли этот аргумент независимой переменной или функцией другой независимой переменной. 47. Производные и дифференциалы высших порядков Пусть производная некоторой функции f дифференцируема. Тогда производная от производной этой функции называется второй производной функции fи обозначается f". Таким образом, f"(x) = (f'(x))'. Если дифференцируема (n - 1)-я производная функции f, то ее n-й производной называется производная от (n - 1)-й производной функции f и обозначается f(n). Итак, f(n)(x) = (f(n-1)(x))', n ϵ N, f(0)(x) = f(x). Число n называется порядком производной. Дифференциалом n-го порядка функции f называется дифференциал от дифференциала (n - 1)-го порядка этой же функции. Таким образом, dnf(x) = d(dn-1f(x)), d0f(x) = f(x), n ϵ N. Если x - независимая переменная, то dx = const и d2x = d3x = ... = dnx = 0. В этом случае справедлива формула dnf(x) = f(n)(x)(dx)n. 48. Функция, заданная параметрически Пусть зависимость между аргументом х и функцией у задана параметрически в виде двух уравнений  где t — вспомогательная переменная, называемая параметром. Найдем производную у'х, считая, что функции (21.1) имеют производные и что функция х=x(t) имеет обратную t=φ(х). По правилу дифференцирования обратной функции где t — вспомогательная переменная, называемая параметром. Найдем производную у'х, считая, что функции (21.1) имеют производные и что функция х=x(t) имеет обратную t=φ(х). По правилу дифференцирования обратной функции  Функцию у=ƒ(х), определяемую параметрическими уравнениями (21.1), можно рассматривать как сложную функцию у=y(t), где t=φ(х). По правилу дифференцирования сложной функции имеем: у'х=y't•t'x. С учетом равенства (21.2) получаем Функцию у=ƒ(х), определяемую параметрическими уравнениями (21.1), можно рассматривать как сложную функцию у=y(t), где t=φ(х). По правилу дифференцирования сложной функции имеем: у'х=y't•t'x. С учетом равенства (21.2) получаем 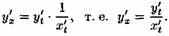 Полученная формула позволяет находить производную у'х от функции заданной параметрически, не находя непосредственной зависимости у от х. 49. Интервалы монотонности. Монотонность функции. Условия монотонности. Оказывается, монотонность функции связана с тем, каков знак ее производной: · Если производная положительна, то функция возрастает · Если производная отрицательна, то функция убывает Полученная формула позволяет находить производную у'х от функции заданной параметрически, не находя непосредственной зависимости у от х. 49. Интервалы монотонности. Монотонность функции. Условия монотонности. Оказывается, монотонность функции связана с тем, каков знак ее производной: · Если производная положительна, то функция возрастает · Если производная отрицательна, то функция убывает
|

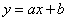
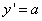
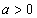 , возрастает
, возрастает 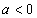 , убывает
, убывает 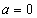 , постоянная
, постоянная 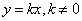
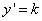
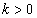 , возрастает
, возрастает 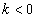 ,убывает
,убывает 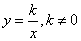
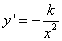
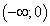 и на
и на 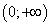
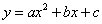
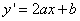
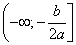 , возрастает на
, возрастает на