Математическое ожидание и дисперсия дискретной случайной величины.
Рассмотрим вопрос о значениях, которые может принимать некоторая величина х в зависимости от случайных, т.е. не поддающихся учету причин. При этом каждое значение xi , полученное в результате единичного испыта-
ния, является случайной величиной, вероятность появления которой pi . Зависимость между значением случайной величины и ее вероятностью называется распределением этой величины.
Характеристикой среднего значения случайной величины служит ма- тематическое ожидание. Математическим ожиданием дискретной случай- ной величины называют сумму произведений всех ее возможных значений на их вероятности:
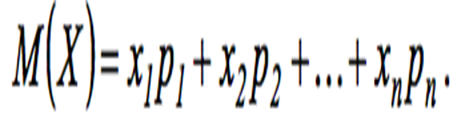
Если случайная величина принимает счетное множество возможных значений, то
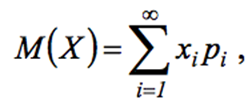 причем предполагается, что ряд, находящийся в правой части равенства, сходится абсолютно и сумма всех вероятностей pi равна единице.
причем предполагается, что ряд, находящийся в правой части равенства, сходится абсолютно и сумма всех вероятностей pi равна единице.
Математическое ожидание обладает следующими свойствами:
1. Математическое ожидание постоянной величины равно самой по- стоянной: M(C)=C.
2. Математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых:
M(X1 +X2 +K+Xn)=M(X1)+M(X2)+K+M(Xn).
3. Математическое ожидание произведения взаимно независимых случайных величин равно произведению математических ожиданий сомно- жителей: M(X1X2KXn)=M(X1)M(X2)KM(Xn).
4. Математическое ожидание биномиального распределения равно произведению числа испытаний на вероятность появления события в одном испытании: M(X)=np.
Характеристиками рассеяния возможных значений случайной величи- ны вокруг математического ожидания служат, дисперсия и среднее квадрати- ческое отклонение. Дисперсией случайной величины Х называют математи-
ческое ожидание квадрата отклонения: D(X )= M [X - M (X )]2 . Дисперсию
удобновычислятьпоформуле D(X)=M(X2)-[M(X)]2.Дисперсияобладает следующими свойствами:
1. Дисперсия постоянной равна нулю: D(C)= 0 .
2. Постоянный множитель можно выносить за знак дисперсии, пред- варительно возведя его в квадрат: D(CX )= C 2 D(X ).
3. Дисперсия суммы независимых случайных величин равна сумме дисперсий слагаемых : D(X1 + X2 +K+ Xn )= D(X1)+ D(X2 )+K+ D(Xn ).
4. Дисперсия биномиального распределения равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании: D(X)=npq.
Средним квадратическим отклонением случайной величины называют квадратныйкореньиздисперсии s(X)= D(X).
Вариационный ряд. Статистическое распределение выборки.
Пусть для изучения колличественного (дискретного или непрерывно- го) признака X из генеральной совокупности извлечена выборка x1,x2,...,xn объёма n. Наблюдавшиеся значения xi признака X называют вариантами, а последовательность вариант, записанных в возрастающем порядке,- вариационным рядом.
Статистическим распределением выборки называют перечень вари- ант xi вариационного ряда и соответствующих им частот ni ( сумма всех час- тот равна объёму выборки n) или относительных частот wi (сумма всех отно- сительных частот равна единице). Статистическое распределение выборки можно задать также в виде последовательности интервалов и соответствую- щих им частот ( в качестве частоты интервала принимают сумму частот вариант, попавших в этот интервал).
Полигон частот.
Полигоном частот называют ломаную, отрезки которой соединяют
точки (x1,n1), (x2,n2),...,(xk,nk), где хi - варианты выборки и ni - соответствую- щие им частоты.
Полигоном относительных частот называют ломаную, отрезки ко- торой соединяют точки (x1,w1), (x2,w2),...,(xk,wk), где хi - варианты выборки и wi - соответствующие им относительные частоты. При непрерывном распре- делении признака весь интервал, в котором заключены все наблюдаемые зна- чения признака, разбивают на ряд частичных интервалов длины h и находят ni - сумму частот вариант, попавших в i-й интервал.
Гистограмма частот.
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длины h, а высоты равны отношению ni/n (плотность частоты). Площадь частичного i-го прямоугольника равна h×ni/n= ni-сумме частот вариант, попавших в i-ый интервал. Площадь гистограммы частот равна сумме всех частот, т.е. объёму выборки n.
Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длины h, а высоты равны отношению wi/h (плотность относительной частоты). Площадь частичного i-го прямоугольника равна (h w)i/h= wi - относительной частоте вариант, попавших в i-ый интервал. Площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. единице.
