Нахождение длины вектора по теореме косинусов.

Большинство задач на нахождение длины вектора решаются в координатах. Однако, когда координаты вектора не известны приходится искать другие пути решения.

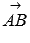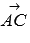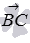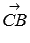Пусть известны длины двух векторов , и угол между ними (или косинус угла), а требуется найти длину вектора или . В этом случае можно по теореме косинусов в треугольнике АВС вычислить длину стороны ВС, которая равна искомой длине вектора.

Разберем решение примера для пояснения сказанного.

Пример.

Длины векторов 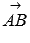и 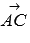равны 3 и 7 соответственно, а угол между ними равен 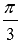. Вычислите длину вектора .

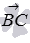Решение.

Длина вектора 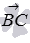равна длине стороны ВС в треугольнике АВС. Из условия нам известны длины сторон АВ и АС этого треугольника (они равны длинам соответствующих векторов), а также угол между ними, поэтому нам достаточно данных для применения теоремы косинусов:

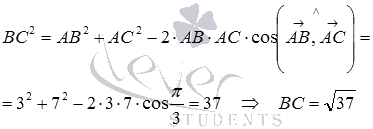
Таким образом, .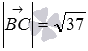

Ответ:

.

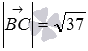Итак, для нахождения длины вектора по координатам используем формулы
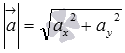или ,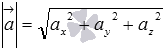
по координатам точек начала и конца вектора -
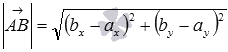или ,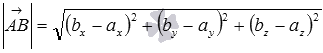
в некоторых случаях к результату приводит теорема косинусов.

16. Линейно зависимые и линейно независимые системы векторов.

Рассмотрим набор из p n-мерных векторов, обозначим их следующим образом 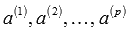. Составим линейную комбинацию этих векторов и произвольных чисел 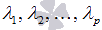(действительных или комплексных): 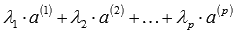. Отталкиваясь от определения операций над n-мерными векторами, а так же свойств операций сложения векторов и умножения вектора на число, можно утверждать, что записанная линейная комбинация представляет собой некоторый n-мерный вектор 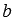, то есть, .

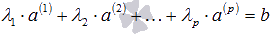Так мы подошли к определению линейной зависимости системы векторов .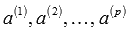

Определение.

Если линейная комбинация 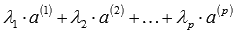может представлять собой нулевой вектор тогда, когда среди чисел 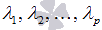есть хотя бы одно, отличное от нуля, то система векторов 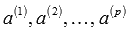называется линейно зависимой.

Определение.

Если линейная комбинация 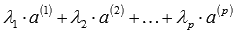представляет собой нулевой вектор только тогда, когда все числа 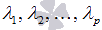равны нулю, то система векторов 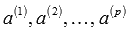называется линейно независимой.

17. Базис пространства R3. Разложение вектора по произвольному базису.

Базис векторного пространства – это упорядоченная совокупность линейно независимых векторов этого пространства, число которых равно размерности пространства.

Приведем некоторые рассуждения, основываясь на этих определениях.

Рассмотрим пространство n-мерных векторов.

Покажем, что размерность этого пространства равна n.

Возьмем систему из n единичных векторов вида

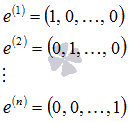
Примем эти векторы в качестве строк матрицы А. В этом случае матрица А будет единичной матрицей размерности n на n. Ранг этой матрицы равен n (при необходимости смотрите статью ранг матрицы: определение, методы нахождения). Следовательно, система векторов 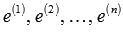линейно независима, причем к этой системе нельзя добавить ни одного вектора, не нарушив ее линейной независимости. Так как число векторов в системе 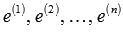равно n, то размерность пространства n-мерных векторов равна n, а единичные векторы 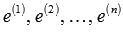являются базисом этого пространства.

Из последнего утверждения и определения базиса можно сделать вывод, что любая системаn-мерных векторов, число векторов в которой меньше n, не является базисом.

Теперь переставим местами первый и второй вектор системы 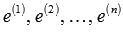. Легко показать, что полученная система векторов 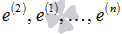также является базисом n-мерного векторного пространства. Составим матрицу, приняв ее строками векторы этой системы. Эта матрица может быть получена из единичной матрицы перестановкой местами первой и второй строк, следовательно, ее ранг будет равен n. Таким образом, система из n векторов 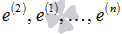линейно независима и является базисом n-мерного векторного пространства.

Если переставить местами другие векторы системы 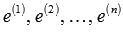, то получим еще один базис.

Если взять линейно независимую систему не единичных векторов, то она также является базисом n-мерного векторного пространства.

Таким образом, векторное пространство размерности n имеет столько базисов, сколько существует линейно независимых систем из n n-мерных векторов.

Если говорить о двумерном векторном пространстве (то есть, о плоскости), то ее базисом являются два любых не коллинеарных вектора. Базисом трехмерного пространства являются три любых некомпланарных вектора.

Рассмотрим несколько примеров.

Пример.

Являются ли векторы 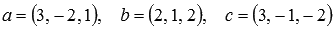базисом трехмерного векторного пространства?

Решение.

Исследуем эту систему векторов на линейную зависимость. Для этого составим матрицу, строками которой будут координаты векторов, и найдем ее ранг:

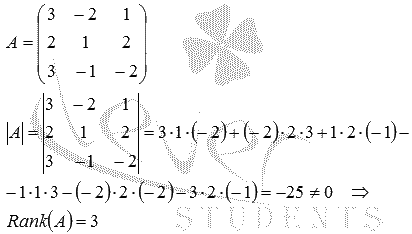
Таким образом, векторы a, b и c линейно независимы и их количество равно размерности векторного пространства, следовательно, они являются базисом этого пространства.

Ответ:

да, являются.

Пример.

Может ли система векторов быть базисом векторного пространства?

Решение.

Эта система векторов линейно зависима, так как максимальное число линейно независимых трехмерных векторов равно трем. Следовательно, эта система векторов не может быть базисом трехмерного векторного пространства (хотя подсистема 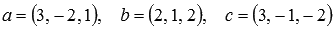исходной системы векторов является базисом).

Ответ:

нет, не может.

Пример.

Убедитесь, что векторы

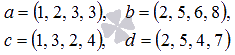
могут быть базисом четырехмерного векторного пространства.

Решение.

Составим матрицу, приняв ее строками исходные векторы:

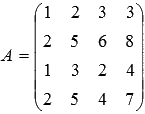
Найдем ранг матрицы методом Гаусса:

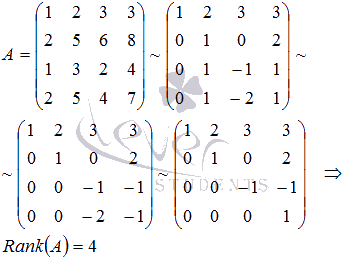
Таким образом, система векторов a, b, c, d линейно независима и их количество равно размерности векторного пространства, следовательно, a, b, c, d являются его базисом.

Ответ:

исходные векторы действительно являются базисом четырехмерного пространства.