Нахождение длины вектора по координатам.

Нахождение длины вектора по координатам.

Длину вектора 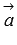будем обозначать 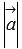. Из-за такого обозначения длину вектора часто называют модулем вектора.

Начнем с нахождения длины вектора на плоскости по координатам.

Введем на плоскости прямоугольную декартову систему координат Oxy. Пусть в ней задан вектор 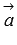и он имеет координаты 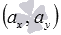. Получим формулу, позволяющую находить длину вектора 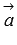через координаты 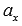и .

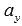Отложим от начала координат (от точки О) вектор 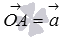. Обозначим проекции точки А на координатные оси как 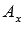и 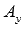соответственно и рассмотрим прямоугольник 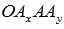с диагональю ОА.

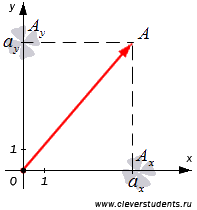
В силу теоремы Пифагора справедливо равенство 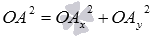, откуда 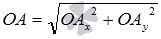. Из определения координат вектора в прямоугольной системе координатмы можем утверждать, что 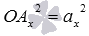и 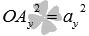, а по построению длина ОА равна длине вектора 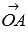, следовательно, .

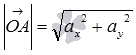Таким образом, формула для нахождения длины вектора 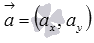по его координатам на плоскости имеет вид .

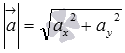Если вектор 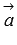представлен в виде разложения по координатным векторам 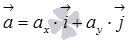, то его длина вычисляется по этой же формуле 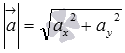, так как в этом случае коэффициенты 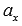и 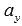являются координатами вектора 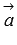в заданной системе координат.

Рассмотрим пример.

Пример.

Найдите длину вектора 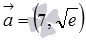, заданного в декартовой системе координат.

Решение.

Сразу применяем формулу для нахождения длины вектора по координатам :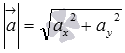

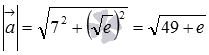
Ответ:

.

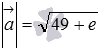Теперь получим формулу для нахождения длины вектора 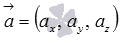по его координатам в прямоугольной системе координат Oxyz в пространстве.

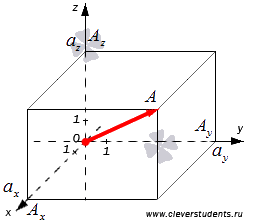
Отложим от начала координат вектор 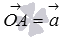и обозначим проекции точки А на координатные оси как 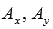и 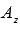. Тогда мы можем построить на сторонах 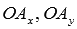и 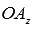прямоугольный параллелепипед, в котором ОА будет диагональю.

В этом случае 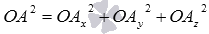(так как ОА – диагональ прямоугольного параллелепипеда), откуда 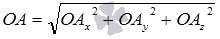. Определение координат вектора позволяет нам записать равенства 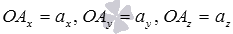, а длина ОА равна искомой длине вектора, следовательно, .

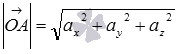Таким образом, длина вектора 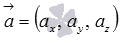в пространстве равна корню квадратному из суммы квадратов его координат, то есть, находится по формуле .

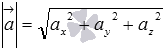Пример.

Вычислите длину вектора 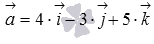, где 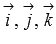- орты прямоугольной системы координат.

Решение.

Нам дано разложение вектора 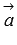по координатным векторам вида 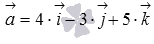, следовательно, 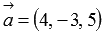. Тогда по формуле нахождения длины вектора по координатам имеем .

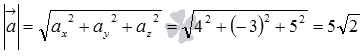Ответ:

.

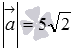Прямая на плоскости

Общее уравнение

Ax + By + C ( 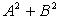> 0).

Вектор 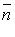= (А; В) - нормальный вектор прямой.

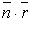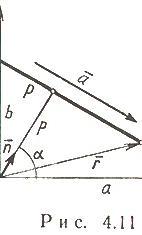
В векторном виде: + С = 0, где 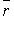- радиус-вектор произвольной точки на прямой (рис. 4.11).

Частные случаи:

1) By + C = 0 - прямая параллельна оси Ox;

2) Ax + C = 0 - прямая параллельна оси Oy;

3) Ax + By = 0 - прямая проходит через начало координат;

4) y = 0 - ось Ox;

5) x = 0 - ось Oy.

Уравнение прямой в отрезках

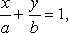
где a, b - величины отрезков, отсекаемых прямой на осях координат.

Нормальное уравнение прямой (рис. 4.11)

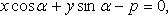
где 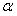- угол, образуемый нормально к прямой и осью Ox; p - расстояние от начала координат до прямой.

Приведение общего уравнения прямой к нормальному виду:

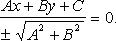
Здесь 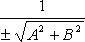- нормируемый множитель прямой; знак выбирается противоположным знаку C, если 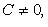и произвольно, если C = 0.

Нахождение длины вектора по координатам.

Длину вектора 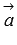будем обозначать 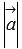. Из-за такого обозначения длину вектора часто называют модулем вектора.

Начнем с нахождения длины вектора на плоскости по координатам.

Введем на плоскости прямоугольную декартову систему координат Oxy. Пусть в ней задан вектор 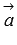и он имеет координаты 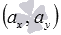. Получим формулу, позволяющую находить длину вектора 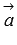через координаты 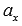и .

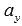Отложим от начала координат (от точки О) вектор 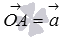. Обозначим проекции точки А на координатные оси как 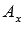и 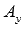соответственно и рассмотрим прямоугольник 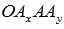с диагональю ОА.

В силу теоремы Пифагора справедливо равенство 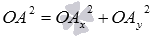, откуда 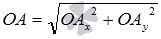. Из определения координат вектора в прямоугольной системе координатмы можем утверждать, что 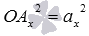и 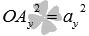, а по построению длина ОА равна длине вектора 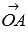, следовательно, .

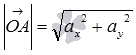Таким образом, формула для нахождения длины вектора 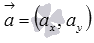по его координатам на плоскости имеет вид .

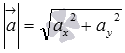Если вектор 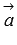представлен в виде разложения по координатным векторам 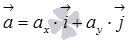, то его длина вычисляется по этой же формуле 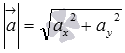, так как в этом случае коэффициенты 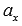и 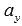являются координатами вектора 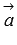в заданной системе координат.

Рассмотрим пример.

Пример.

Найдите длину вектора 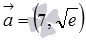, заданного в декартовой системе координат.

Решение.

Сразу применяем формулу для нахождения длины вектора по координатам :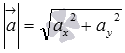

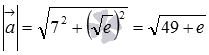
Ответ:

.

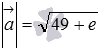Теперь получим формулу для нахождения длины вектора 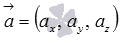по его координатам в прямоугольной системе координат Oxyz в пространстве.

Отложим от начала координат вектор 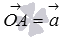и обозначим проекции точки А на координатные оси как 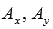и 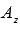. Тогда мы можем построить на сторонах 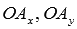и 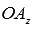прямоугольный параллелепипед, в котором ОА будет диагональю.

В этом случае 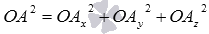(так как ОА – диагональ прямоугольного параллелепипеда), откуда 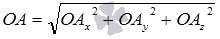. Определение координат вектора позволяет нам записать равенства 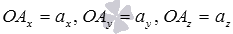, а длина ОА равна искомой длине вектора, следовательно, .

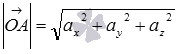Таким образом, длина вектора 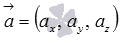в пространстве равна корню квадратному из суммы квадратов его координат, то есть, находится по формуле .

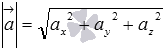Пример.

Вычислите длину вектора 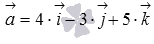, где 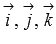- орты прямоугольной системы координат.

Решение.

Нам дано разложение вектора 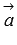по координатным векторам вида 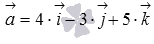, следовательно, 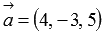. Тогда по формуле нахождения длины вектора по координатам имеем .

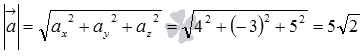Ответ:

.
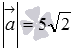