Плоский поток, если в полубесконечном
И круглом пластах расположена одна скважина.
Влияние на производительность скважины
Формы внешнего контура пласта
- Прямолинейный внешний контур
Представим пласт, ограниченный прямолинейным контуром бесконечно большого протяжения Оy через который поступает жид кость или газ (рис. 21). В пласте имеется единственная эксплуатационная скважина с центром в О1 на расстоянии 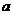 от контура Оу.
от контура Оу.
На контуре питания Оу значение потенциальной функции 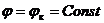
на контуре скважины 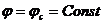 ; радиус скважины
; радиус скважины 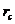 .
.
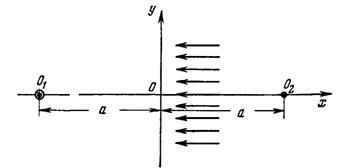 Поскольку контур питания пласта Оу является эквипотенциальной линией, все линии тока, сходящиеся в центре скважины О1,. должны быть перпендикулярными к прямой Оу. Пласт, изображенный на рис. 21 в виде левой полуплоскости, оказывается как бы носителем фильтрационного потока от прямолинейного контура Оу к точечному стоку Ох.
Поскольку контур питания пласта Оу является эквипотенциальной линией, все линии тока, сходящиеся в центре скважины О1,. должны быть перпендикулярными к прямой Оу. Пласт, изображенный на рис. 21 в виде левой полуплоскости, оказывается как бы носителем фильтрационного потока от прямолинейного контура Оу к точечному стоку Ох.
Рис. 21 Схема расположения скважины в пласте с прямолинейным контуром питания.
Но картину фильтрационного поля в левой полуплоскости рис. 21 можно получить, применив зеркальное отображение точки О1 относительно прямой Оу и поместив в точке — отображения О2 источник с дебитом, равным дебиту стока О1. Следовательно, задача о фильтрационном потоке в пласте с прямолинейным контуром питания и с одиночной эксплуатационной скважиной сводится к задаче о совместном действии стока и источника равной производительности, т. е. к задаче, рассмотренной в § 2. Задача, решенная в § 2, отличается от поставленной здесь задачи только граничными условиями. В самом деле, в задаче § 2 контуром питания пласта является контур нагнетательной скважины О2. В данном же случае источник О2 воображаемый, а фактическим контуром питания служит прямая Оу на рис. 21. Однако это не мешает нам использовать найденное уже выражение потенциальной функции (VII.7).
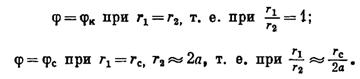 Такой метод решения задачи называется методом отображения. В данном случае сток отображен источником. Как увидим, сток может отображаться стоком, источник — источником.
Такой метод решения задачи называется методом отображения. В данном случае сток отображен источником. Как увидим, сток может отображаться стоком, источник — источником.
Учтем, что
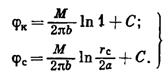 Подставив последовательно соответствующие граничные значения
Подставив последовательно соответствующие граничные значения 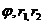 в равенство (VII.7), получим:
в равенство (VII.7), получим:
(VII.22)
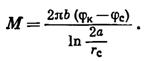 Вычитая почленно второе равенство (VII.22) из первого и решая полученное уравнение относительно М, найдем, что
Вычитая почленно второе равенство (VII.22) из первого и решая полученное уравнение относительно М, найдем, что
(VII.23)
Такова формула массового дебита одиночной скважины в пласте с прямолинейным контуром питания.
- Круговой внешний контур и эксцентрично заложенная скважина
Выражение потенциальной функции, использованное при решении задачи о скважине в пласте с прямолинейным контуром, можно применять и при решении задачи для скважины О1, заложенной в пласт с круговым внешним контуром Вк при условии, что она расположена эксцентрично относительно окружности контура Вк (рис. 22). В этом случае радиус внешнего контура пласта, являющийся также эквипотенциальной линией, можно определить по уравнению (VII.8).
Пусть радиус контура питания пласта Вк равен 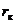 а радиус эксплуатационной скважины О1 —
а радиус эксплуатационной скважины О1 — 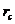 ; расстояние скважины от центра
; расстояние скважины от центра 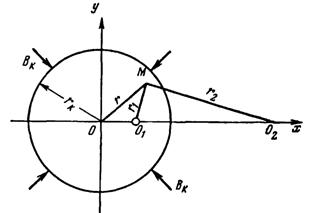 контура питания (зксцентриситет) равен
контура питания (зксцентриситет) равен 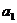 . По формуле (VII.11а) определяем значение постоянной С1, соответствующее данному контуру радиуса
. По формуле (VII.11а) определяем значение постоянной С1, соответствующее данному контуру радиуса 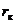 . В данном случае
. В данном случае 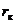 обозначает величину R формулы (VII.11а).
обозначает величину R формулы (VII.11а).
Граничные условия задачи:
по формулам (VII.8) и (VII.11а) на контуре питания:
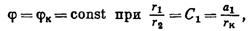 |
Рис. 22. Схема расположения скважины в(VII.23)
