Границы применимости линейного закона фильтрации

Так же как и для гранулярных (пористых) сред, при больших скоростях фильтрации линейный закон фильтрации может нарушаться из-за появления значительных по величине сил инерции. Выражение для числа Рейнольдса в трещиноватой среде может быть представлено в следующем виде:

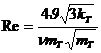(III.12)

Отметим, что согласно сказанному, за нижнюю границу нарушения линейного закона фильтрации в трещиноватом пласте следует принять 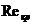= 0,4. Понятно, что если линейный закон фильтрации не действителен для трещиноватых пластов, следует использовать нелинейные законы.

Аналитически нелинейные законы выражаются в виде одночленных и двучленных формул. Одночленная формула предполагает следующую запись:

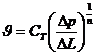, (III.13)

где 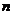изменяется от 1 до 1,75 (по данным проф. Г. М. Ломизе).

Значение постоянной С_Т можно получить методами теории подобия, оно равно

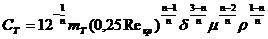, (III.14)

где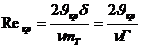

На основании (III.14) уравнение (III.13) можно записать в виде:

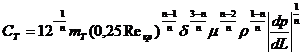, (III.15)

где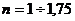

При 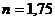имеем турбулентный режим. Если линейный закон нарушается, используется двучленная формула, учитывающая возрастающую роль сил инерции в связи с увеличением скоростей движения жидкостей и газов:

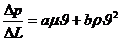, (III.16)

где 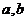— некоторые постоянные.

Б. Ф. Степочкиным на основе обработки обширного экспериментального материала (по результатам опытных данных и заимствованного из различных литературных источников) для большого диапазона размеров (от нескольких микрон до 75 мм) твердых частиц разнообразной формы (слагающих продуктивные пласты) и интервала чисел Rе от 10^-6 до 10³ получена двучленная формула:

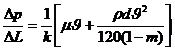, (III.17)

где d — диаметр зёрен, составляющих среду.

Согласно сказанному ранее, трещиноватую среду можно представлять в виде укрупнённой пористой среды, где зёрнами являются блоки породы, а поровыми каналами — трещины.

Следовательно, уравнение (III.17) применительно к трещиноватой среде с учётом поправочного коэффициента по Г. М. Ломизе запишется в виде:

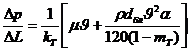, (III.18)

где 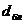— средний линейный размер блока. Поправка 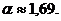Для трещиновато-пористого пласта рассматривается скорость фильтрации в пористых блоках и в системе трещин. При этом в системе трещин нарушение линейного закона происходит раньше, чем в пористых блоках. Причем для фильтрации жидкости, газа в пористых блоках критериальная оценка нарушения линейного закона Дарси осуществляется на основании зависимостей, приведенных в главе II.

Глава IV

ПРОСТЕЙШИЕ ЗАДАЧИ ОДНОМЕРНОГО ПОТОКА

В ПОРИСТОЙ СРЕДЕ

Одномерный фильтрационный поток.

Потенциальное движение

Установившийся фильтрационный поток в пласте, в котором давление можно выразит в функции только одной линейной координаты, считается одномерным.

Представим себе в пористой или трещиноватой среде трубку тока переменного сечения (рис. 8) и допустим, что во всех сечениях, нормальных по отношению к кривой — оси трубки, площади сечения 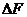выражаются в функции длины 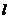, отсчитываемой вдоль оси трубки

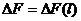. (IV.1)

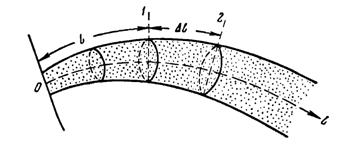Рис. 8. Схема трубки тока в фильтрующей среде.

Пусть каждая нормальная к оси трубки поверхность является изобарической, т. е. поверхностью равного давления р. Если трубка тока неизменяема, давление можно считать зависящим только от одной линейной координаты 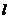, а следовательно, поток — одномерным.

Из условия неразрывности потока следует, что при установившейся одномерной фильтрации расход массы жидкости в единицу времени через все изобарические поверхности в трубке тока будет один и тот же.

Введём алгебраическую величину – массовую скорость фильтрации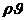

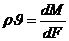,(IV.2)

где М — расход массы жидкости через поверхность равного давления; его мы можем назвать массовым дебитом. Полный установившийся фильтрационный поток можно рассматривать как непрерывную совокупность неизменяемых трубок тока, а массовый дебит М — как сумму расходов через соответствующие поверхности сечений всех этих трубок тока.

С другой стороны, в соответствии с законом Дарси (II.17) модуль массовой скорости фильтрации 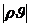можно записать так:

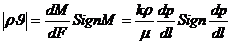, (IV.3)

где 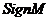и 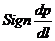— символы, показывающие, что в равенстве (IV.3) следует ставить тот знак, какой имеет в первом случае М, во втором 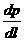. (Латинское signum — знак).

Из равенства (IV.3) получим:

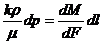. (IV.4)

Равенство (IV.4) применимо к несжимаемой или малосжимаемой жидкости, газу, газированной и многофазной жидкости. В случаях сжимаемой жидкости или газа плотность 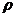изменяется в зависимости от давления р. Абсолютная вязкость 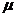зависит также от давления р. Коэффициент проницаемости фильтрующей среды 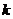при неоднородности этой среды или неоднородности жидкости, а также при проявлении упругих свойств оказывается непостоянным, изменяющимся в зависимости от давления р.

Из этого следует, что множитель 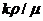левой части равенства (IV.4) в общем случае является переменным вдоль потока и его можно выразить в функции давления р.

После интегрирования (IV.4) найдем

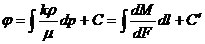, (IV.5)

где 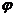— функция, которую мы назовем потенциальной (потенциалом); С и С’ — постоянные интегрирования.

Из (IV.5) видно, что 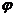может выражаться или в функции давления р, или же в функции линейной координаты 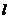. Это объясняется тем, что р, как уже говорилось, однозначно определяется .

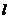Учитывая на основании (IV.4) и (IV.5), что левую часть равенства (IV.4) можно записать в виде

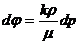, (IV.6)

представим равенство (IV.3) так:

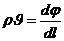. (IV.7)

Это есть уравнение закона фильтрации для любой жидкости или газа в случае существования потенциальной функции в одномерном потоке. Движение флюида при существовании потенциальной функции (IV.5) называется потенциальным.

Итак, на основании (IV.7) можем определить потенциальное движение жидкости, газа или их смеси в пористой или трещиноватой среде как такое, при котором массовая скорость фильтрации равна градиенту потенциальной функции. Как видим, формула (IV.7) обобщает закон Дарси для потенциального движения жидкости, газа или их смеси.

В самом деле, массовая скорость фильтрации оказывается пропорциональной величине градиента такой функции 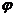, которая определяется зависимостью параметров 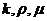, от давления р. Ранее же, формулируя в § 4 главы II закон Дарси, мы полагали, что скорость фильтрации зависит только от одной переменной — от величины градиента давления.

Подсчитаем массовый дебит. С этой целью возьмем формулы (IV.2) и (IV.7) и приравняем между собой правые их части. Умножаем затем обе части полученного равенства на 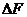и, проинтегрировав, находим:

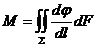, (IV.8)

где 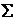— поверхность, массовый расход жидкости, газа или их смеси через которую равен М.

Примечание. Функцию, аналогичную 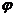, для случая движения газа и смеси нефти и газа в пласте использовал акад. Л. С. Лейбензон в своей монографии, опубликованной в 1934 г. Чтобы получить функцию, введённую Л. С. Лейбензоном, достаточно в подынтегральной функции (IV.5) положить 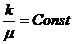и только множитель 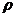считать переменным. (Лейбензон брал объёмный вес γ).