Матрицы. линейные операции над матрицами.

МАТРИЦЫ. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД МАТРИЦАМИ.

Матрицей называется прямоугольная таблица чисел, содержащая m-строк одинаковой длины и n-столбцов одинаковой длины. Матрица записывается в виде:

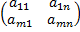где a_ij ÎR 1 £ i £ m 1 £ j £ n

Обозначают матрицу А, В, С, или сокращают. A_3x2 B_mxn A = (a_ij)_3x4

Числа, составляющие матрицу, называют элементами матрицы и обозначают . a_ij, где i – номер строки, j – номер столбца.

Матрицы называются равными, если они одинаковых размеров, и на одинаковыъ позициях стоят одинаковые элементы.

Матрица, все элементы которой равны 0, называется нулевой и обозначается 0_mxn.

Матрица, у которой число строк m равно числу столбцов n, называется квадратной. Квадратную матрицу размера mxn называют матрицей n-ого порядка. A_n

Элементы квадратной матрицы, у которой номер столбца равен номеру строки, называются диагональными и образуют главную диагональ.

Квадратная матрица, у которой все элементы кроме элементов главной диагонали равны нулю, называется диагональной. Диагональная матрица, у которой все диагональные элементы равны, называется скалярной. Скалярная матрица, у которой на диагонали стоят единицы, называется единичной матрицей. E = E_n

Если в квадратной матрице все элементы, лежащие ниже или выше главной диагонали равны нулю, то такая матрица называется треугольной. a_ij=0, i>j верхняя треугольная

a_ij=0, i<j нижняя треугольная

Линейные операции над матрицами – сложение, умножение на число.

Сложение матриц. Вводится только для матриц одинаковых размеров. Определение. Пусть A = (a_ij)_mxn B = (b_ij)_mxn – 2 матрицы одинаковых размеров. Суммой двух матриц А и В одинакового размера называется матрица, обозначаемая A+B такая, что (A+B)_mxn = (a_ij+b_ij)_mxn . таким образом, сложение матриц осуществляется покомпонентно.

Умножение матрицы на число. Определение. Пусть A = (a_ij)_mxn и αÎR. Произведением матрицы A на число называется матрица, обозначаемая αА, такая, что (αА)_mxn = (αa_ij)_mxn.. т.е. каждый элемент которой получен умножением соответствующего элемента матрицы А на число. Следствие: общий множитель всех элементов матрицы можно вынести за знак матрицы.

Матрица равная – А = (-1)А называется противоположной матрице А. Разность матрицы можно определить как А-В=А+(-В)

Свойства:

1. А+В=В+А

2. (А+В)+С=А+(В+С)

3. А-А=А+(-А)=О

4. 0А=О

5. 1А=А

6. α(А+В)=αА+αВ

7. (α+β)А=αА+βА

8. α(βА)=(αβ)А

УМНОЖЕНИЕ МАТРИЦ.

Упорядоченная пара (А, В) двух матриц называется согласованно, если число столбцов первой матрицы А равно числу строк второй матрицы В. В частности, согласованы в любом порядке 2 квадратные матрицы одного размера. Умножать можно только согласованные пары в порядке их согласования.

Произведением двух согласованных матриц называется матрица, каждый элемент которой равен сумме произведений элементов i-ой строки матрицы А на соответствующий элемент j-ого столбца матрицы В.

Произведение n-экземпляров квадратной матрицы А АхА......А = Аⁿ называется n-ной степенью.

Свойства произведения матриц:

1. А(ВС)=(АВ)С

2. (А+В)С=АС+ВС

3. С(А+В)=СА+СВ

4. α(АВ)=(αА)В=А(αВ)

5.ЕА = АЕ = А

СВОЙСТВА ОПРЕДЕЛИТЕЛЕЙ

Каждой квадратной матрице можно поставить в соответствие число, которое называется определителем, которое обозначается d(A) или = detA

1. Для матрицы A₁ = (a)

Det(a) = |a| = a

2. A₂ =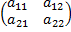

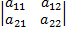= a₁₁a₂₂ – a₁₂a₂₁

3. detA₃ = a₁₁a₂₂a₃₃ + a₁₂a₂₃a₃₁ + a₂₁a₃₂a₁₃ – a₁₃a₂₂a₃₁ – a₁₂a₂₁a₃₃ – a₂₃a₃₂a₁₁

свойства определителей.

1. Det(AB) = det(A)det(B)

2. detA = detA^T Определитель матрицы равен определителю транспонированной матрицы, т.е. любое верное утверждение относительно строк определителя остается верным и для столбцов

3. общий множитель любой строки (столбца) определителя можно вынести за знак определителя, т.о. если у определителя имеется нулевая строка (столбец), то он равен нулю.

4. Если у определителля поменять местами любые две строки (столбца), то он изменит знак на противоположный, т.е. если у определителя 2 одинаковых (пропорциональные) строки (столбца), то он равен нулю.

5. Если каждый элемент строки/столбца представлен в виде суммы 2ух слагаемых, то этот определитель равен сумме 2ух определителей.

6. Если к одной троке определителся прибавить любую другую строку, умноженную на любое число, то он не изменится.

ОБРАТНАЯ МАТРИЦА.

Понятние обратной матрицы существует только для квадратных матриц.

Определение. Пусть а – квадратная матрица. Матрицей, обратной А, называется матрица, обозначаемая А^-1, такая что АА^-1 = А^-1А = Е, где Е – единичная матрица.

Квадаратная матрица называется невырожденной, если ее определитель отличен от нуля, и вырожденной – в противном случае.

Теорема: для того, чтобы квадратная матрица А имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля.

Доказательство. Есть А^-1 Û detA¹0

Необходимость. У А есть А^-1

Надо доказать что detA¹0

Т.к. АА^-1 = Е => det(AA^-1) = detE => detAdetA^-1 = detE. Т.е. detAdetA^-1=1 =>detA¹0

Достаточность. Дано: detA¹0. Надо доказать что существует А^-1

Схема построения обратной матрицы.

1. Находим detA=d¹0

2. Находим все алгебраические дополнения A_ij

3. Строим матрицу А^с = (A_ij)^T

4. A^-1 = (1/detA)A^c

Если обратная матрица существует, то она единственная. Действительно. A, detA¹0 и пусть B, C – две обратные к А.

Рассмотрим. BAC = (BA)C = EC = C => B=C

B(AC) = BE = B

Понятие обратной матрицы позволяет решать т.н. матричные ур-я вида АХ = В, где А, В – заданные матрицы, Х – неизвестная матрица.

Действительно. Если |A|¹0 , то есть A^-1 умножим: A^-1(AX) = A^-1B => X=A^-1B

Аналогично: XA = B, X=BA^-1

Или: AXB = C => X = A^-1CB^-1

СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ. КОМПЛАНАРНОСТЬ ТРЕХ ВЕКТОРОВ.

Смешанным произведением 3х векторов a,b,c называется число [a,b]c , полученное скалярным умножением векторного произведения [a,b] на третий вектор с. обозначается abc = (a,b,c) = [a,b]c

Пусть {a,b,c} – правая тройка.

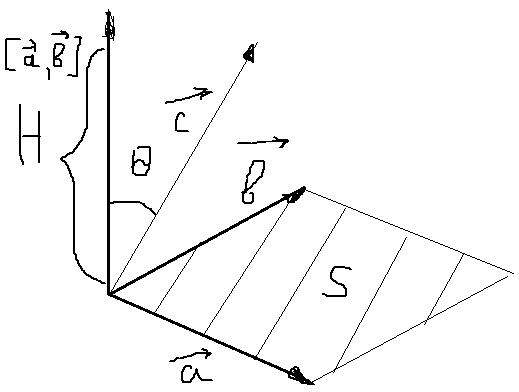
Тогда abc = [a,b]c = |[a,b]||c|cosq q - угол между [a,b] и c

abc = Sпараллелограмма|c|cosq = Sпараллелограмма H = V паралелипипеда, построенного на этиъ векторах.

Если {a,b,c} – левая тройка, то abc = -V

Свойства:

1. a[b,c] = [a,b]c

2. abc = cab = bca = -bac = -cab = -acb

3. (a₁ + a₂)bc = a₁bc + a₂bc

4. (aa)bc = a(ab)c = ab(ac) = aabc

Вычисление смешанного произведения

Пусть a(a_x, a_y, a_z) b(b_x, b_y, b_z) c(c_x, c_y, c_z) abc - ?

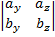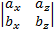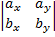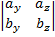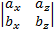abc = [a,b]c = ( , - , )(c_x, c_y, c_z) = c_x - c_y + c_z =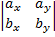

=

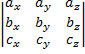
Т.е. abc = [a,b]c =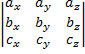

Формулировка: для того, чтобы 3 вектора были компланарны, необходимо и достаточно, чтобы их смешанное произведение равнялось нулю.

Необходимость: дано: 3 вектора компланарны, доказать: abc = 0

Если a,b,c компланарны, то [a,b]^c => abc = [a,b]c = 0

Достаточность. Дано: abc = 0, доказать: a,b,c – компланарны.

0 = abc = [a,b]c = |[a,b]||c|cosq = |a||b|sinj|c|socq = 0

1. |a| или |b| или |c| равны 0 => среди векторов есть нулевой вектор => a,b,c компланарны

2. sinj = 0 => a||b => a,b,c компланарны

3. cosq=0 => c^[a,b] = p/2 => с принадлежит плоскости ab

применение смешанного произведения

1. вычисление объемов параллелипипедов ( V = |abc|), трегольных призм ( V = |abc|/2), пирамид ( V = |abc|/6)

2. определение компланарности трех векторов

ЧИСЛО Е.

Неравенство Бермули (1+a)ⁿ>= 1+na, a>-1

Теорема. Последовательность x_n = (1+1/n)ⁿ сходится, т.е. имеет предел.

Доказательство:

Рассмотрим

Ясно также, что y_n>0 при всех nÎN, т.к. y_n ограничена.

По предыдущей теореме

Пределом x_n = (1+1/n)ⁿ называется число е = 2,718281828459045

е играет огромную роль в анализе, а сам предел называется вторым замечательным пределом. Логарифм по основанию числа е называют натуральным логарифмом.

ТЕОРЕМЫ О ПРЕДЕЛАХ ФУНКЦИИ.

Теорема1. Для существования предела ф-ии f(x) в точке x₀ необходимо и достаточно существование обоих односторонних пределов в этой точке и их равенство.

Теорема2. Если функция f(x) и g(x) определены в некоторой окрестности точки x₀ и для всех xÎO(x₀) имеет место неравенство f(x)<=g(x), то lim_x->x0f(x)<= lim_x->x0g(x) если они существуют.

Теорема3. Пусть в окрестности точки x₀ – O(x₀) определены ф-ии f(x), j(x), y(x) и f(x)£ j(x)£ y(x)

Предположим, что существует 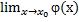= =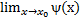A

Тогда существует 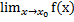= A

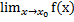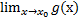Теорема4. Пусть = A и = B

Тогда:

1. 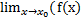± 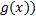= A ± B

2. 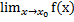g(x) = AB

3. 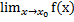/g(x) = A/B, B¹0

1. lim сf(x) = c lim f(х), если с – const, постоянную величину можно вынести за знак предела;
2. lim хⁿ = (lim x)ⁿ:
3. lim ⁿÖx = ⁿÖlim x.

ДИФФЕРЕНЦИАЛ. ИНВАРИАНТНОСТЬ ФОРМЫ.

limy=A, y=A+a

limDy/Dx=y`, Dy/Dx=y`+a, Dy=y`Dx+aDx

Dx®0

Dy=y`Dx+e, где e-б.м.в., величина более высокого порядка малости,, чем Dx(a), и ее можно отбросить.

dy=y`Dx

Дифференциалом ф-ции наз. величина, пропорциональная б.м. приращению аргумента Dх и отличающаяся от соответствующего приращения ф-ции на б.м.в. более высокого порядка малости, чем Dх.

Если y=x, то dy=dx=x`Dx=Dx, dx=Dx

Если y¹x, то dy=y`dx, y`=dy,dx

Геометрический смысл: дифференциал - изменение ординаты касательной, проведенной к графику ф-ции в точке (x₀,f(x₀)) при изменении x₀ на величину Dx

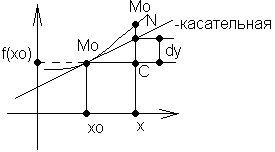
Св-ва:
1. (U±V)`=U`±V`, то (U±V)`dx=U`dx±V`dx, d(U±V)=d(U±V)

2. (UV)`=U`V+V`U, то (UV)`dx=V`dU+U`dV

3.d(c)=c`dx=0*dx=0

4. d(U/V)`=(V`dU-U`dV)/V².

ИНВАРИАНТНОСТЬ:

Дифференциал ф-ии всегда равен произведению производной и дифференциала аргумента и не зависит от то, является ли аргумент независимой переменной или промежуточной функцией.

АССИМПТОТЫ ГРАФИКА ФУНКЦИИ.

ассимптоты бывают 2х видов – вертикальные и наклонные.

Определение. Прямая x=x₀ называется вертикальной ассимптотой графика ф-ии y=f(x) если хотя бы один из односторонних пределов ф-ии f(x) в точке x₀ равен +(-) бесконечность.

Ясно, что непрерывная на всей оси ф-я вертикальных ассимптот не имеет.

Определение. Прямая y=kx+b называется наклонной ассимптотой (при к=0 – горизонтальной) графика ф-ии y=f(x) при x стремящемся к +(-) бесконечности, если ф-ию f(x) можно представить в виде:

F(x) = kx + b + a(x), где a(x) стремится к 0 при х стремящемся к +(-) бесконечности.

Если такое представление возможно только при х стремящемся к +бесконечности, то соответствующая наклонная ассимптота называется правой (-бесконечности – левой).

Теорема.

Для того, чтобы график ф-ии y=f(x) имел наклонную ассимптоту y=kx+b необходимо и достаточно чтобы существовали конечные пределы.

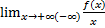= k

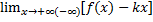И = b

ФОРМУЛА ТЕЙЛОРА.

МАТРИЦЫ. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД МАТРИЦАМИ.

Матрицей называется прямоугольная таблица чисел, содержащая m-строк одинаковой длины и n-столбцов одинаковой длины. Матрица записывается в виде:

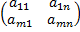где a_ij ÎR 1 £ i £ m 1 £ j £ n

Обозначают матрицу А, В, С, или сокращают. A_3x2 B_mxn A = (a_ij)_3x4

Числа, составляющие матрицу, называют элементами матрицы и обозначают . a_ij, где i – номер строки, j – номер столбца.

Матрицы называются равными, если они одинаковых размеров, и на одинаковыъ позициях стоят одинаковые элементы.

Матрица, все элементы которой равны 0, называется нулевой и обозначается 0_mxn.

Матрица, у которой число строк m равно числу столбцов n, называется квадратной. Квадратную матрицу размера mxn называют матрицей n-ого порядка. A_n

Элементы квадратной матрицы, у которой номер столбца равен номеру строки, называются диагональными и образуют главную диагональ.

Квадратная матрица, у которой все элементы кроме элементов главной диагонали равны нулю, называется диагональной. Диагональная матрица, у которой все диагональные элементы равны, называется скалярной. Скалярная матрица, у которой на диагонали стоят единицы, называется единичной матрицей. E = E_n

Если в квадратной матрице все элементы, лежащие ниже или выше главной диагонали равны нулю, то такая матрица называется треугольной. a_ij=0, i>j верхняя треугольная

a_ij=0, i<j нижняя треугольная