Матрицы и определители. Линейные операции над матрицами

Матрицей называется прямоугольная таблица размером m х n, и состоящая из m строк и nстолбцов

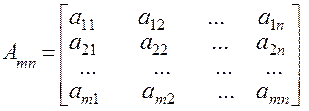Числа a_ij , i=1,m,j=1,n, входящие в данную таблицу, называются

матричными элементами, а индексы i и j элементауказывают

(соответственно) номера строки и столбца, в которых расположен элемент a_ij.

Если m=n, то матрица называется квадратной. Квадратная матри­ца из n строк и n столбцов, называется матрицей n-го порядка.

Каждой матрице порядка n ставится в соответствие число, которое называет­ся определителем или детерминантом этой матрицы и обозначается од­ним из следующих символов

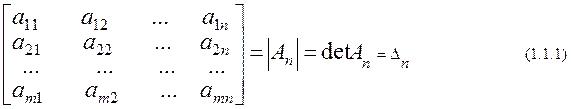
Числа a_ij (i,j=1,n)называются элементами определителя.

Если определитель матрицы равен 0, то матрица называется осо­бенной (вырожденной), а если определитель отличен от 0 - то матри­ца неособенная (невырожденная).

Квадратная матрица называется симметрической, если a_ij = a_ji,

т.е. равны элементы, симметричные относительно главной диагонали, т.е. главная диагональ, образована элементами a_ji , i=1,n .

Диагональной называется матрица, у которой все элементы, не принадлежащие главной диагонали, равны 0.

Единичная матрица - это диагональная матрица, у которой все элементы главной диагонали равны 1. Обозначается единичная матрица буквами Е или I.

Пример 1.1.1.

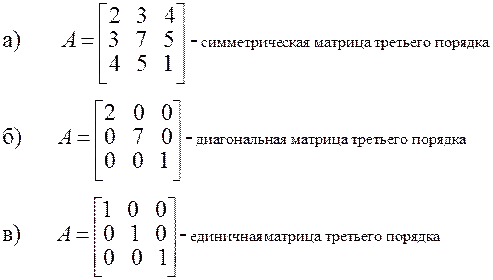
Две матрицы А и В называются равными, если они имеют одина­ковые размерности и равные соответствующие элементы.

Матрица А^Т , полученная из данной матрицы А заменой каждой её строки столбцом с тем же номером, называется транспонированной от­носительно А . Если матрица А имеет размеры m х n, то матрица А^Т имеет размеры n х m.

Пример 1.1.2.

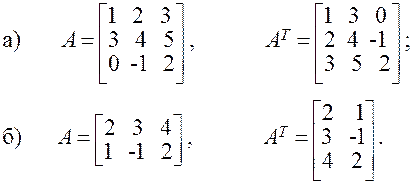
Линейными операциями над матрицами называются операции сложе­ния (вычитания) и умножения на число. Сложение и вычитание опреде­ляется только для матриц одинаковых размеров.

Суммой (разностью) двух матриц А={a_ij}_mn и В={b_ij}_mn называется

матрица С={c_ij}_mn, для которой c_ij= a_ij ± b_ij ,i=1,m,j=1,n.

Произведением матрицы А={a_ij}_mnна число αназывается матрица

В= α {a_ij}_mnдля которой b_ij =α a_ij , i=1,m,j=1,n.

Пример 1.1.3.

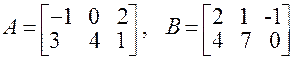Даны матрицы

и числоα = 4. Вычислить матрицы: С=А+В, D=A-B, М = А4

Умножение матриц А и В, т.е. получение произведения этих матриц С = АВ, возможно лишь в том случае, когда число столбцов матрицы А равно числу строк матрицы В. Такие матрицы называются согласованными.

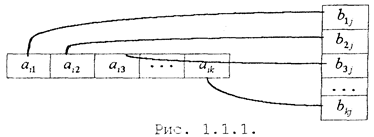
Произведением двух согласованных матриц А_mk={a_ij}_mk и В_kn={b_ij}_kn

называется такая третья матрица С_mn={c_ij}_mn для кoторой каждый элементc_ij ,i=1,m,j=1,n вычисляется по формуле (рис. 1.1.1.):

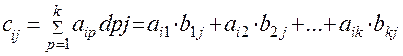
Пример 1.1.4. Вычислить произведение матриц

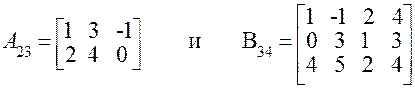
Можно ли получить произведение BA ?

Число столбцов матрицы A(3) равно числу строк матрицы В(3).

Поэтому произведение АВ= С определено. Матрица С имеет размер­ность 2х4, а её элементы вычисляются по формуле (1.1.2).

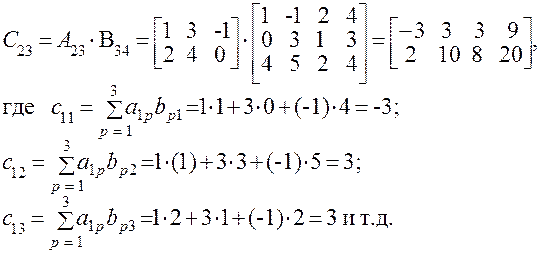Произведение B∙A не определено, т.к. число столбцов матрицы B(4) не равно числу строк матрицы А(2).

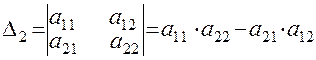
Определителем (1.1.1) матрицы второго порядка называется число

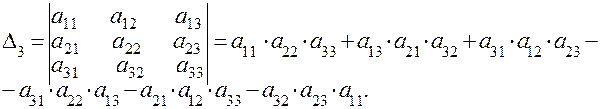Определителем матрицы третьего порядка называется число

Студенту следует обратить внимание на правила треугольника вычисления определителей третьего порядка. Пример 1.1.5. Вычислить определитель

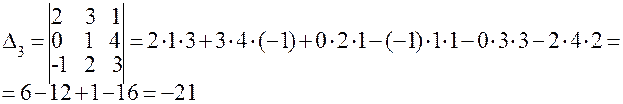
Минором М _ij (i, j=1,n) элемента а_ij определителя называется опре­делитель, который получается из данного определителя вычеркиванием строки и столбца, на пересечении которых находится элемент а_ij .

Алгебраическим дополнением А_ij(i, j=1,n) элемента а_ij определи­теля называется его минор взятый со знаком (-1)^i+j, т.е.

А_ij=(-1)^i+j M_ij (1.1.3)

Пример 1.1.6. Записать миноры и алгебраические дополнения элементов определителя примера 1.1.5.

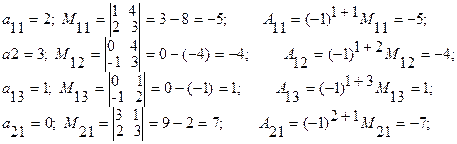
и т.д. Всего можно записать 9 миноров и 9 алгебраических дополне­ний элементов и определителя матрицы третьего порядка.

Замечание Определители матриц n-го порядка (n =1,2...) короче называют определителями n-го порядка.

Свойства определителей:

1) определитель не изменится, если транспонировать матрицу опреде­лителя;

2) при перестановке двух соседних строк (столбцов) определитель меняет знак;

3) определитель с двумя одинаковыми строками (столбцами) равен 0;

4) общий множитель для элементов строки (столбца) можно вынести за знак определителя;

5) определитель равен 0 , если все элементы строки (столбца) равны нулю;

6) определитель не изменится, если к элементам строки (столбца), прибавить элементы другой строки (столбца), предварительно умно­жив их на один и тот же множитель;

7) определитель равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения

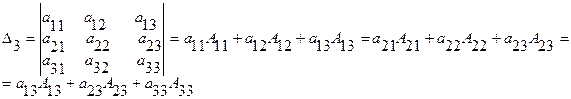Например:

Пример 1.1.7. Вычислить определитель примера 1.1.5., исполь­зуя свойство 7 определителей (разложение произвести по элементам первого столбца)

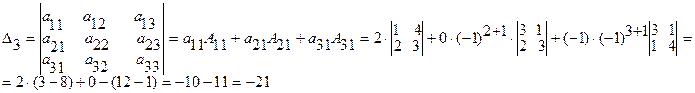
По аналогии с формулой (1.1.4) вводятся определители n-го по­рядка

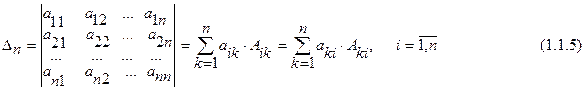
Пример 1.1.8. Используя свойства 1-7 определителей, вычислить определитель четвертого порядка

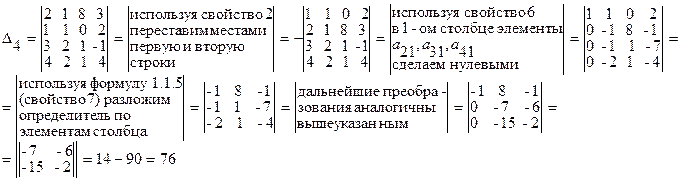
Матрицей, обратной к матрице А, называется квадратная матри­ца А^-1, такая что A^-1 А = Е

Если матрица А невырожденная (det A¹O), то обратная матрица А^-1 находится по формуле

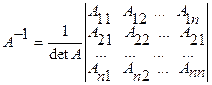
где A_ij (i, j =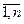
1,n)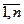

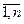
- алгебраические дополнения элементов а_ij (1.1.3)

Пример 1.1.9. Найти матрицу, обратную к данной матрице

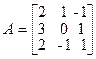
Вычислим определитель матрицы А

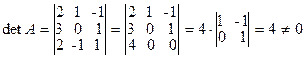
По формуле (1.1.6) находим (вычисление алгебраических допол­нений элементов матрицы А рассмотрено в примере 1.1.6):

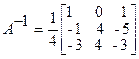
Проверка :

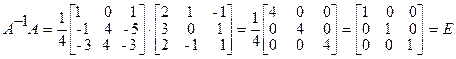
Студентам рекомендуется провести вычисление обратной матрицы методом элементарных преобразований.

Ранг матрицы

Рангом матрицы А размерности т х п называется наибольший из порядков её миноров, отличных от нуля. Если ранг матрицы A равен r, то это означает, что в матрице А имеется отличный от нуля ми­нор порядка r , но всякий минор порядка большего, чемr, равен 0. Ранг матрицы обозначается r(А).

Свойства ранга матрицы А размерности т´ п

1) 0 ≤ r ≤ rnin(m,n);

2) r =0 тогда и только тогда, когда матрица нулевая;

3) для квадратной матрицы n-го порядка r=n тогда и только тогда, когда матрица невырожденная;

4) ранг транспонированной матрицы равен рангу исходной матрицы;

5) ранг матрицы не изменится, если вычеркнуть (дописать) нулевую строку (столбец);

6) ранг матрицы не изменится, если к элементам строки матрицы при­бавить элементы другой строки матрицы, предварительно умноженные на некоторое число;

7) ранг матрицы не изменится, если переставить любые строки (столбцы) матрицы.

Пример 1.1.9. Найти ранг матрицы А

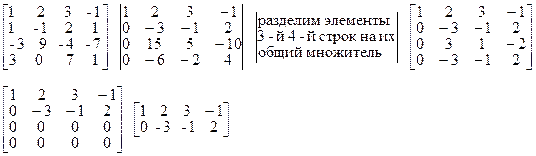
RgA=2 т.к. имеется отличный от нуля определитель второго порядка,

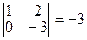например