Уравнение Бесселя и цилиндрические функции

16.1. Первоначальные сведения.В дальнейшем при рассмотрении электромагнитных полей в областях с круговой симметрией встретится обыкновенное дифференциальное уравнение вида

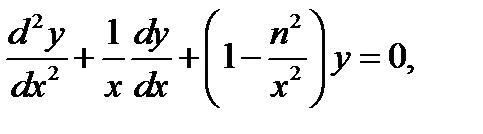(16.1)

которое называется уравнением цилиндрических функций, или уравнением Бесселя n-го порядка. Ниже сообщаются некоторые сведения о его решениях, цилиндрических функциях.Поскольку вы достаточно знакомы с тригонометрическими и экспоненциальными функциями, являющимися решениями уравнения

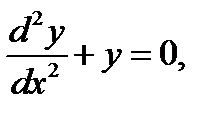(16.2)

то начнём с замечания, что это уравнение при некоторых ограничениях можно рассматривать как предельную форму уравнения Бесселя (16.1) при х ® ∞. Ввиду указанного обстоятельства, между различными решениями обоих уравнений существует соответствие; это поможет понять роль цилиндрических функций в разных задачах, а также их взаимные соотношения. Частным решениям уравнения (16.2) cosx, sinx соответствуют следующие частные решения уравнения (16.1):

J_n (х)- функция Бесселя n-го порядка,

N_n (x) -.функция Неймана n-го порядка.

Точно так же частным решениям (16.2) e^jx, е^-ix соответствуют частные решения уравнения (16.1):

H⁽¹⁾_n(х)- функция Ханкеля 1-го рода п-го порядка,

Н⁽²⁾_n(х)- функция Ханкеля 2-го рода п-го порядка.

На рис. 16.1 приведены графики некоторых из цилиндрических функций. Подобно тому, как 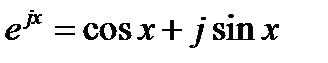, 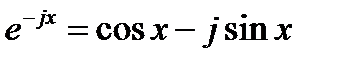имеют место соотношения

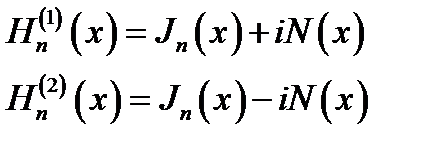(16.3)

Цилиндрические функции не являются периодическими (как, например, тригонометрические функции вещественного аргумента), однако это «осциллирующие», колеблющиеся функции. Функции J_n(x)и N_n(x)с возрастанием положительного х принимают значения, колеблющиеся около нуля с монотонно убывающей амплитудой. Их графики создают впечатление деформированных тригонометрических кривых.

Полезно помнить, что

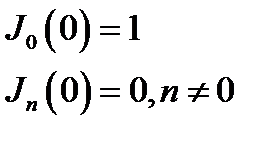, (16.4)

и 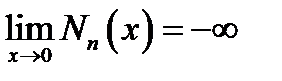(16.5)

Подобно общим решениям у = Acosx + Bsinx и y = Pe^-jx + Qe^jx, уравнения (16.2) имеют общие решения уравнения Бесселя (16.1) в виде:

y = AJ_n(x) + BN_n(x) (16.6а)

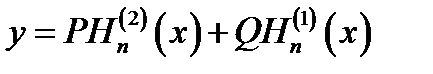. (16.б)

Обычно требуется, чтобы решение задачи удовлетворяло условию ограниченности |у| < ∞. Соответственно этому, если в рассмотрение входит точка х = 0, то общее решение уравнения Бесселя (16.1) ввиду (16.5) имеет вид:

y = AJ_n(x).(16.7)

Действительно, единственная возможность получения ограниченного решения ,на отрезке, включающем нуль, состоит в том, что неопределённый коэффициент В в (16.6а) полагается равным нулю.

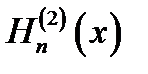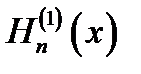16.2. Асимптотические представления. При неограниченно возрастающем аргументе J_n(x)и N_n (x)переходят в тригонометрические функции, и - в экспоненциальные:

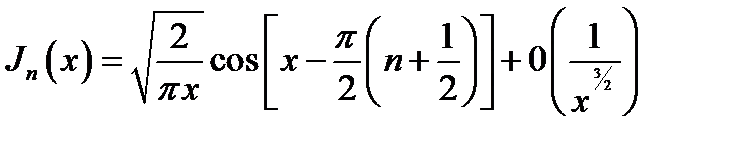(16.8)

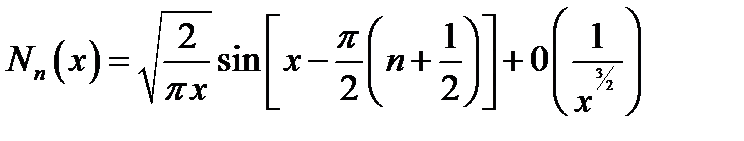(16.9)

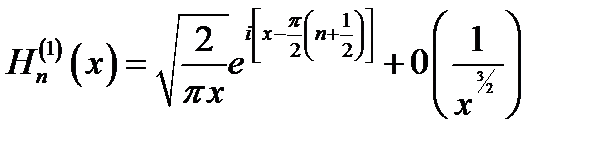(16.10)

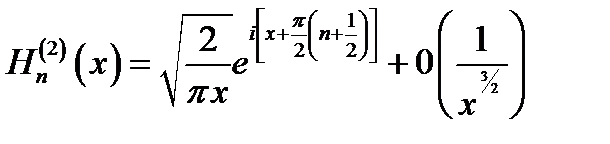(16.11)

Напомним (п. 9.3), что употребленный здесь символ 0 (...) означает величину, убывающую при х → ∞ как функция, заключённая в скобки (в данном случае 1/х^3/2).

Весьма существенно следующее. Пусть х = kz,и решение уравнения Бесселя (16.1) должно иметь характер комплексной амплитуды волны, распространяющейся в сторону возрастания z. Тогда оно выражается функцией Ханкеля второго рода, т. е. получается из (16.6б) при Q = 0:

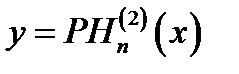(16.12)

Это вытекает из приведенных асимптотических представлений (16.10), (16.11).

16.3. Степенные ряды; представления функций малого аргумента. Функции. Бесселя представляются степенными рядами вида:

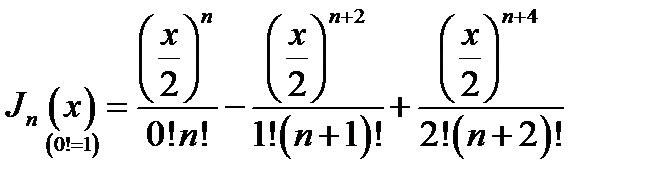(16.13)

В частности,

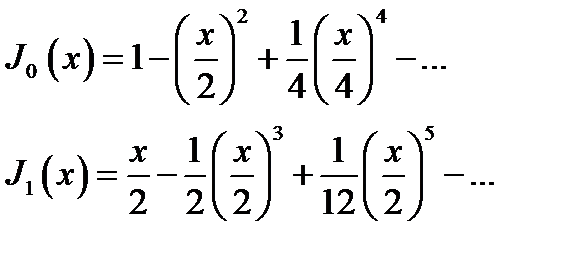(16.13а)

Поэтому при |х | << 1

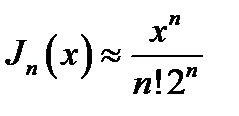(16.14)

В частност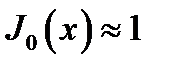и,

и 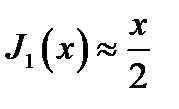(16.14а)

Ввиду громоздкости ряд для функций Неймана мы не приводим. При |х|<< 1 эти функции представляются в виде:

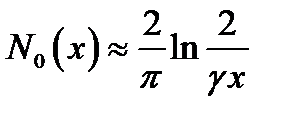и 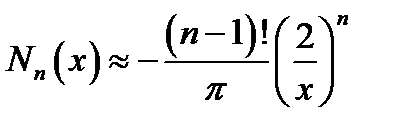, (16.15)

(γ = 1,781…).

16.4. Функциональные соотношения. Запишем ещё ряд употребительных формул, используя символ Z_n(x)для обозначения произвольной цилиндрической функции (формулы верны при подстановке в качестве Z_n(x)функций Бесселя, Неймана или Ханкеля).

Для натурального п

Z_-n(x) = (-1)ⁿZ_n(x).(16.16)

В частности,

Z_-1 (x) = - Z_t(x). (16.16a)

В справедливости (16.16) для функций Бесселя нетрудно убедиться на основании ряда (16.13).

При дифференцировании цилиндрических функций пользуются соотношениями:

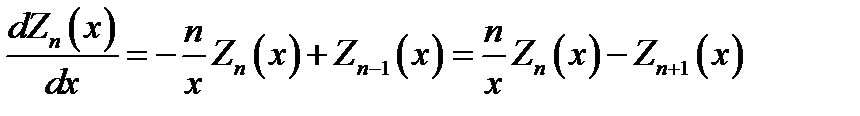(16.17)

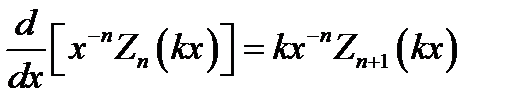, (16.18)

а также 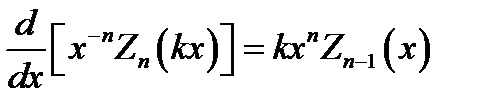. (16.19)

Из (16.17) следует:

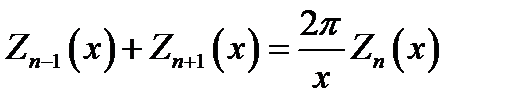. (16.20)

Для n = 0 и n = 1 из (16.17) получаем:

Z₀(x) = - Z_t (x) и 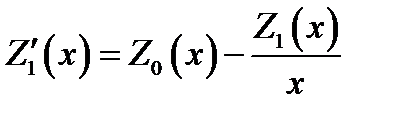. (16:21)

Запишем также некоторые неопределённые интегралы, содержащие цилиндрические функции:

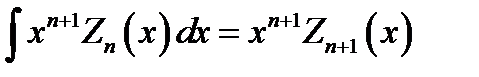; (16.22)

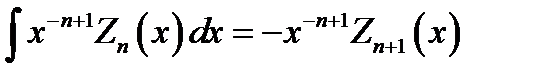(16.23)

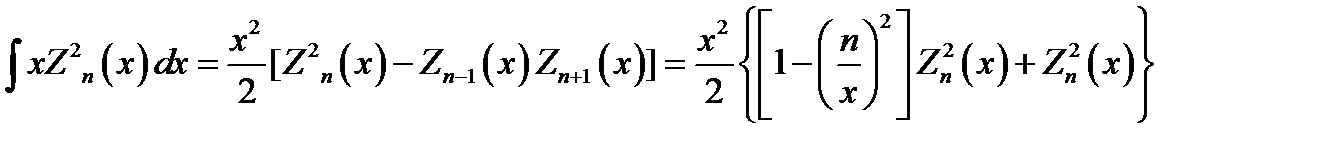; (16.24)

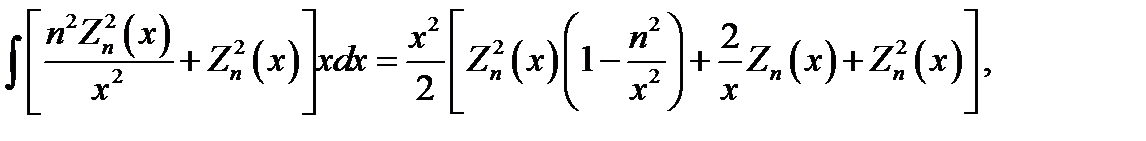(16.25)

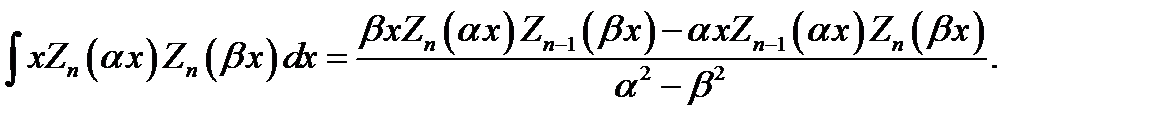
Эти формулы нетрудно проверить, используя приведенные ранее дифференциальные соотношения.

16.5. Интегральное представление функций Бесселя. Функции Бесселя J_n(x) при целом п могут быть представлены в виде:

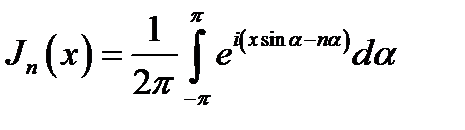(16.27)

Это интегральное представление в дальнейшем будет играть важную роль. Мы используем его также для частичного обоснования ранее приведенных соотношений.

Убедимся сначала, что (16.27), действительно, выражает решение уравнения Бесселя (16.1). С этой целью произведем в (16.27) интегрирование по частям и получим:

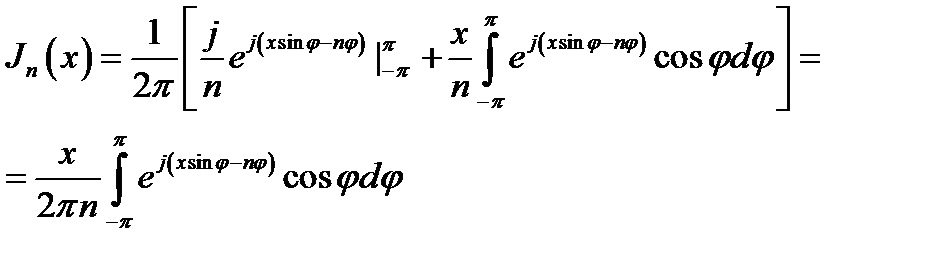(16.28)

(первый член в квадратных скобках уничтожается).

Далее вычислим производную J'_n(x) и также преобразуем полученное выражение путём интегрирования его по частям:

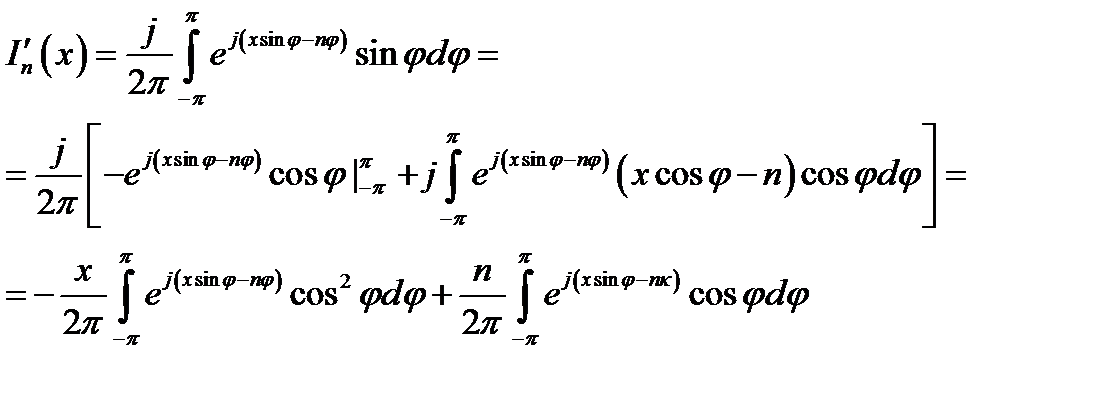(16.29)

Вторая производная J"_n(x) имеет вид:

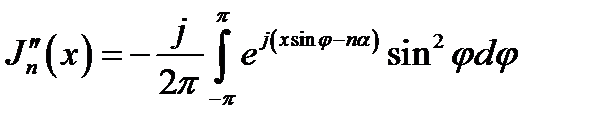. (16.30)

Внося (16.28), (16.29) и (16.30) в уравнение (16.1), имеем тождество:

,

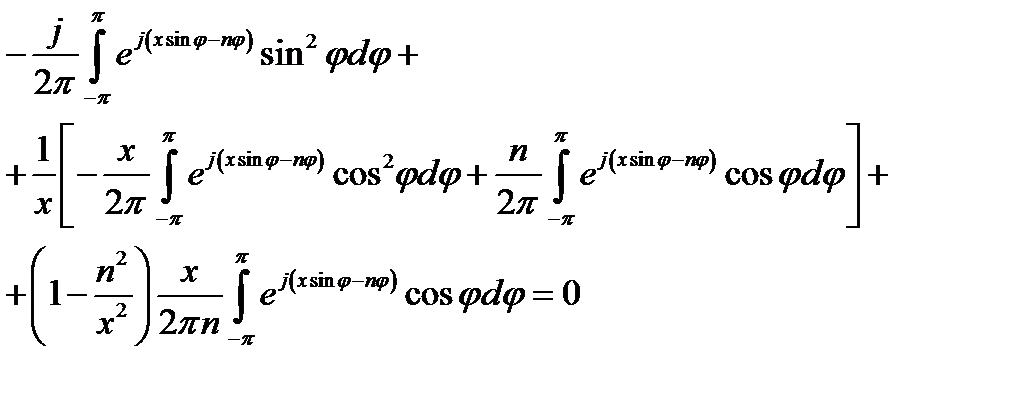в чём немедленно убеждаемся после элементарных преобразований с привлечением (16.27) и (16.28).

Используя интегральное представление (16.27), нетрудно проверить приведенные в п. 4 дифференциальные соотношения. Покажем это на примере формулы (16.17). Согласно (16.27)

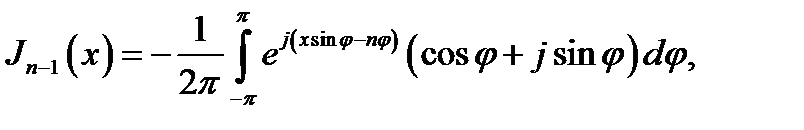
т. е. можно написать:

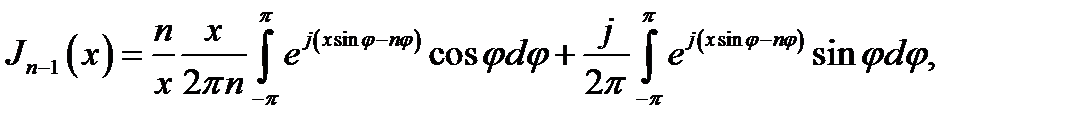
что с учётом (16.28) и (16.29) дает:

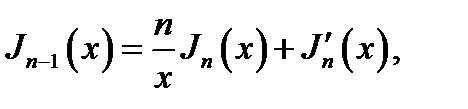
а это совпадает с первым из равенств (16.17) при Z_n (х) =J_n(x).

16.6. Разложение по функциям Бесселя. Далее начнём с рассмотрения ряда Фурье некоторой функции f (φ), определённой на отрезке 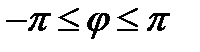, по функциям e^jna. Вы можете получить этот ряд, заменив в (12.22) V(t)на f(φ) и положив ω = 1. Таким образом, имеем:

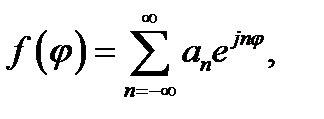. (16.31а)

где

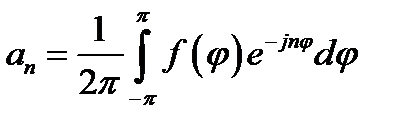(16.31б)

Особый интерес для нас представляет функция f(φ) = e^jxsinφ. Внося её в (16.316) и учитывая интегральное представление (16.27), имеем: a_n= J_n(x). Ряд Фурье (16.31а) функции e^jxsinφ следовательно, имеет вид:

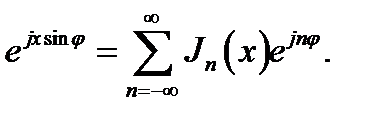(16.32)

Получено разложение, содержащее функции Бесселя всех целых порядков.

Выведем ещё важную модификацию разложения (16.32). Заменяя слева и справа от знака равенства φ на 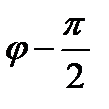, находим:

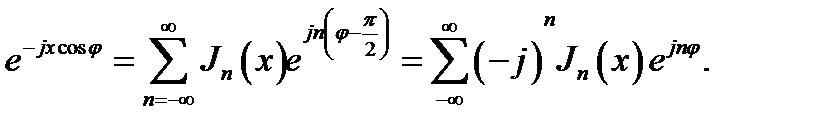(16.33)

Этот результат может иметь, например, следующее применение. Пусть вдоль оси z распространяется плоская однородная волна, комплексная амплитуда которой изменяется, как e^-jkz. Введём цилиндрическую систему координат (рис. 16.2), в которой z = rcosφ, так что e^-jkz = e^-jkrcosφ. Поэтому, делая в (16.33) замену х → kr находим:

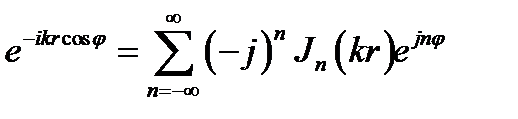. (16.34)

Это разложение плоской однородной волны по гармоникам J_n(kr)e^ina, которые можно истолковать как бегущие по азимуту φ (по часовой стрелке или против неё в зависимости от знака п)плоские неоднородные волны.

Разложение (16.32) можно применить для получения степенного ряда (16.13). Обозначив e^-jα = p, перепишем (16.32) в виде:

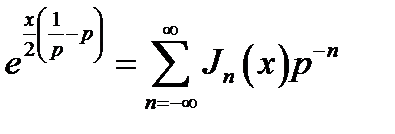(16.35)

Левую часть будем рассматривать как произведение функци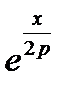й и 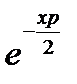, которые можно разложить в степенные ряды:

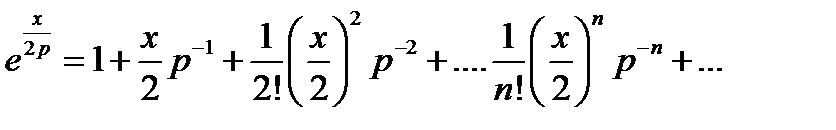
и

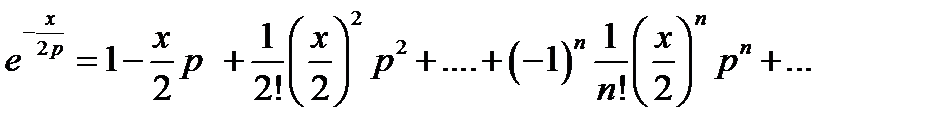
Перемножая ряды и выделяя коэффициенты при степенях р^-k в получаемом произведении, приравняем их соответствующим коэффициентам в правой части (16.35), т. е. функциям Бесселя J_k(х); это и должно привести к (16.13). Например, для получения разложения J₀(х)надо перемножить лишь члены рядов с одинаковыми номерами:

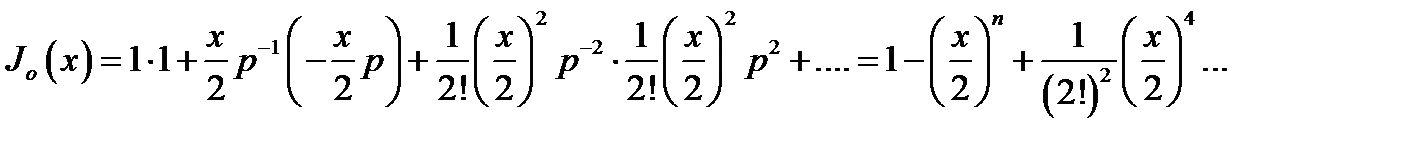
Как видно, результат совпадает с соответствующим рядом (16.13а).

Для нахождения ряда (16.13) при любом порядке функции Бесселя п >0 надо каждый (m + n) -ый член разложения 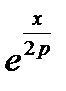умножить на m-ый член разложения 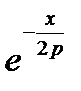просуммировать от т = 0. Это даёт:

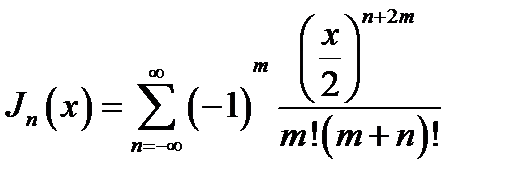(16.36)

Мы получили краткую запись ряда (16.13).

17. Решение однородного уравнения Гельмгольца
методом разделения переменных

17.1. Декартовы координаты. Однородное уравнение Гельмгольца будет встречаться в дальнейшем при постановке разных граничных задач. Случай декартовых координат является простейшим, и поэтому именно с него начинается изложение. Уравнение Гельмгольца

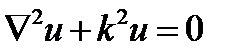(17.1)

при использовании декартовой системы координат (х, у, z)принимает вид:

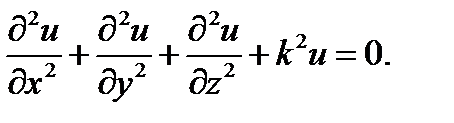(17.2)

Рассмотрим получение его решений методом разделения переменных (п.11.1).

Ожидаемое решение и = и(х, у, z)представляется в виде произведения

и(х, у, z) = X(x)Y(y)Z(z), (17.3)

где Х(х), Y(y)и Z(z) - функции координат х, у, и z соответственно. Подставим представление (17.3) в уравнение (17.2) и разделим все члены на u = XYZ. Это дает:

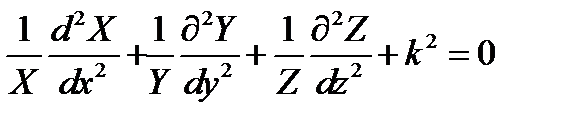. (17.4)

Как видно, первые три члена - функции разных аргументов, а третий постоянен. Это дает основание (§11 п. 1) положить каждую из указанных функций константе; назвав введённые константы 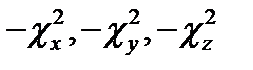,получаем три обыкновенных дифференциальных уравнения:

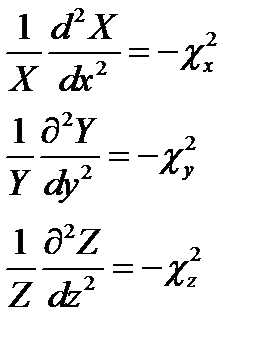, причём 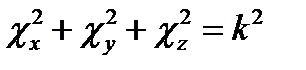(17.5)

Это уже много раз встречавшиеся уравнения типа (7.7) с решениями (7.8). Таким образом, сразу можно выразить решение (17.3) уравнения (17.2):

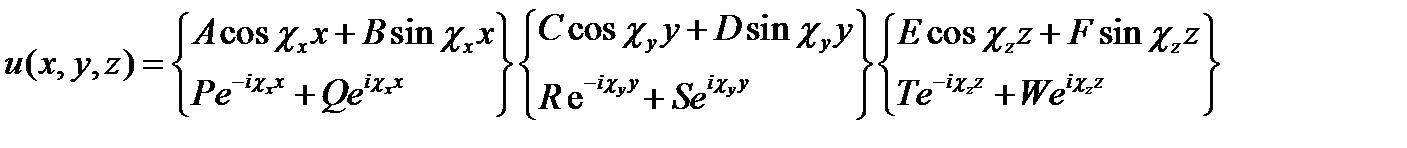(17.6)

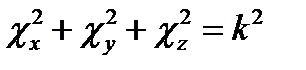
Данная символическая запись означает, что каждый из сомножителей решения (X, Y и Z) можно брать как в форме верхней строчки, так и в форме нижней. Очевидно, что записанная функция (17.6) выражает решение уравнения (17.2) при любых постоянных коэффициентах А, В, ..., Т, W и любых «постоянных разделения» 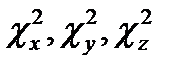, подчинённых равенству в нижней строке.

В случае двумерного уравнения Гельмгольца

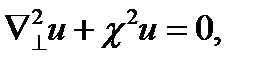(17.7)

записываемого в декартовых координатах как

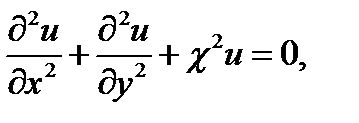(17.8)

имеем:

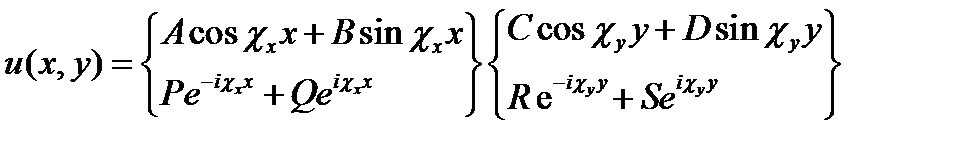(17.9)

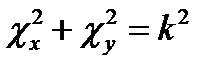
17.2. Цилиндрические координаты.В цилиндрической системе координат (r, φ, z) согласно (6.17) уравнение (17.1) примет вид:

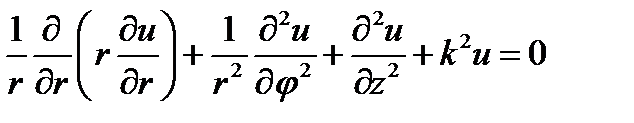(17.10)

Полагая

и(r, φ, z) = U(r) W(φ)Z(z) (17.11)

где U (r), W(φ)и Z(z) - функции координат r, φ и z соответственно. В результате подстановки (17.11) в (17.10) и деления на и = UWZ получаем:

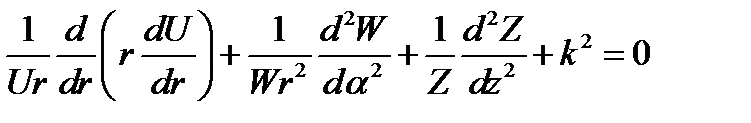(17.12)

Третий член есть функция только координаты z и, таким образом, независим от предыдущих. Это дает основание (§ 11 п. 1) положить его равным некоторой постоянной; последнюю обозначим - χ²_z. Оставшиеся слева члены в сумме также равны постоянной величине, а именно 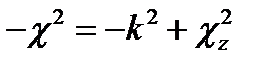. Поэтому имеем следующие уравнения:

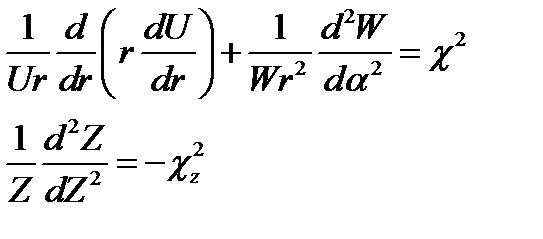
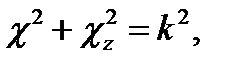(17.13)

эквивалентные вместе первоначальному уравнению (17.12).

Далее произведём операцию разделения переменных в первом из уравнений (17.13), которое после умножения всех членов наr² принимает форму:

.

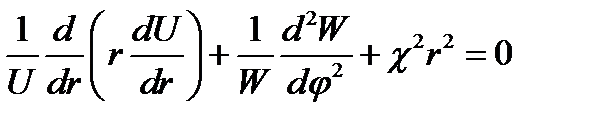Второй член (функция φ) не зависит от первого и третьего (функций r). Поскольку сумма всех членов - нуль, введём, как делалось в п. 11, постоянные п² и - п², которые в сумме равны нулю, и получим:

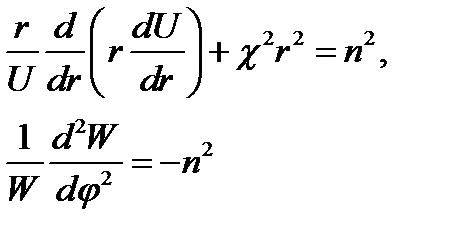(17.14)

Легко убедиться, что в первой строчке (17.14) мы имеем не что иное, как уравнение Бесселя относительно U как функции аргумента χr. Действительно, после дифференцирования по r и умножения всех слагаемых на U/χ² имеем:

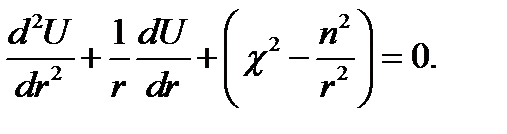(17.15)

Оно совпадает с уравнением (16.1) при замене х на χr.

Итак, объединяя результаты (17.13) и (17.14) с учётом (17.15), получаем совокупность следующих обыкновенных дифференциальных уравнений, эквивалентную уравнению Гельмгольца (17.10):

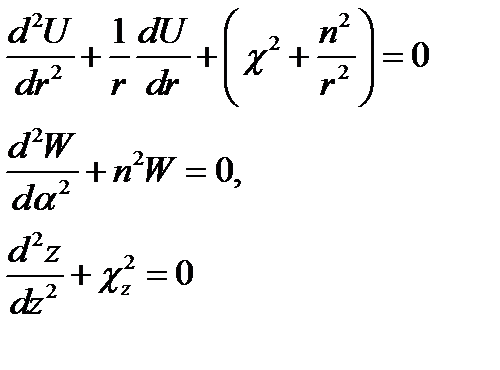
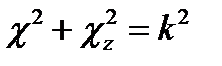(17.16)

Общие решения их известны, причём каждое можно записать в двух формах: с использованием функций Бесселя и Неймана или Ханкеля для первого уравнения согласно (16.6а, б) и с использованием функций тригонометрических или экспоненциальных - для двух последних уравнений. Таким образом, находим следующее выражение и = UWZ:

u(r, φ_,z) =

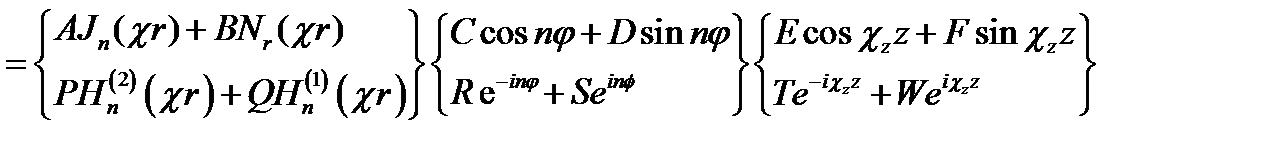17.17

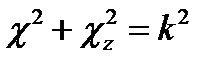
Форма записи имеет тот же смысл, что и в (17.6); аналогично также значение входящих в выражение постоянных.

Обычно область, в которой ищется решение, не ограничена по углу φ. В этом случае М(r, φ, z) и М(r, φ + 2π, z) - это одна и та же точка наблюдения, а следовательно, u (r, φ, z) и и (r, φ + 2π, z) выражают решение в одной и той же точке, т. е. должно быть:

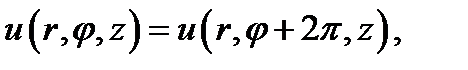, (17.18)

что возможно только при целом п (или равном нулю): п = 0, ±1, ±2, ....

При отсутствии зависимости по z уравнение Гельмгольца (17.1) записывается в форме (17.7), т. е. в цилиндрических координатах:

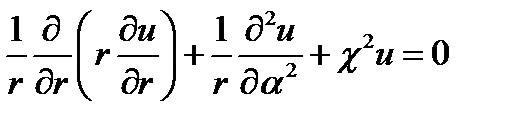. (17.19)

Его решение имеет вид:

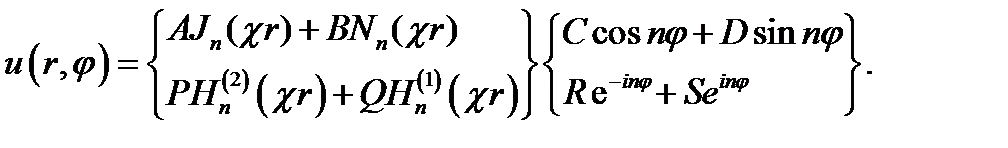(17.20)

Выбор того или иного варианта решения определяется граничными условиями конкретной электродинамической задачи.