Операции в криволинейных координатах

6.1. Криволинейные ортогональные координаты.В декартовой системе координат положение в пространстве некоторой точки М(х', у', z') определяется пересечением трёх взаимно перпендикулярных координатных плоскостей(рис. 6.1)

х = х', у = у', z = z'.

Через точку М, таким образом,, проходят три прямые, каждая из которых принадлежит двум координатным плоскостям. Они называются координатными прямыми;положение точки на каждой из них зависит от одной координаты х, у или z. Произвольно перемещая точку М в пространстве, можно построить сколько угодно координатных плоскостей и соответствующих координатных прямых. Изменению положения точки М соответствует изменение направленного отрезка 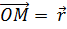, соединяющего её с началом координат О, т. е. радиус-вектора (I.1.3).

Понятно, что точка в пространстве может быть с тем же успехом определена как пересечение трех произвольных однозначно заданных поверхностей. Так, в цилиндрическойсистеме координат фиксируется пересечение поверхности кругового цилиндра и двух плоскостей, одна из которых проходит через его ось, а другая ей перпендикулярна.В сферическойсистеме пересекаются полуплоскость, поверхность конуса и поверхность сферы. Мы пришли, таким образом, к понятию координатных поверхностей.Последние в общем случае можно описать уравнениями

q₁(x, у, z) = const, q₂(x, у, z) = const и q₃(x, у, z) = const, (6.1)

где в левых частях равенств стоят некоторые однозначные функции декартовых координат.

На линии пересечения двух координатных поверхностей выполняются одновременно два равенства из (6.1), а следовательно, её точки определяются только одной из функций q₁, q₂, q₃. Поэтому каждая такая линия называется координатной,а эти функции - криволинейными координатами.

Для произвольной точки М в системе криволинейных координат устанавливается обозначение М (q₁, q₂, q₃).

В каждой точке можно рассматривать единичные векторы (орты), касательные координатным линиям и направленные в сторону возрастания соответствующих координат; они будут обозначены символами .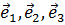

В дальнейшем мы будем использовать только ортогональныесистемы координат, т. е. такие, орты которых в любой точке взаимно перпендикулярны:

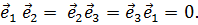(6.2)

Перемещениеточки М выражается приращением её радиус-вектора 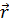. Разлагая дифференциал 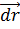no opтам 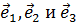, имеем:

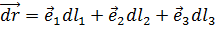, (6.3)

где dl₁, dl₂ и dl₃ - дифференциалы длины по соответствующимкриволинейным координатам.

С другой стороны,

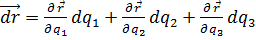. (6.4)

Причём частные производные радиус-вектора по координатам - это векторы, параллельные их ортам:

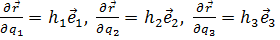. (6.5)

Сопоставляя равенства (6.3) и (6.4) с учётом (6.5), видим, что дифференциалы длины криволинейных координат отличаются от дифференциалов самих координат множителями h₁, h₂ и h₃:

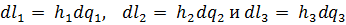. (6.6)

Множители эти называются метрическими коэффициентами,или коэффициентами Ламэ.Вообще метрические коэффициенты являютсяфункциями координат. В тех случаях, когда приращения длины иприращения соответствующих координат идентичны, этикоэффициенты равны единице.

Заметим, что если в криволинейных координатах рассматривается поле вектора

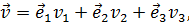
то дифференциал длины силовой линии выражается в отличие от (2.6) по формуле (6.3) и, соответственно, вместо пропорции (2.7) получается:

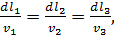(6.7)

или подставляя (6.6):

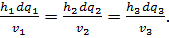(6.8)

6.2. Цилиндрические и сферические координаты. Из всех ортогональных криволинейных систем координат чаще всего иcпользуют цилиндрическую и сферическую, которые мы уже упоминали. Цилиндрические координаты r, φ, z (см. рис. 6.2) - это расстояние точки наблюдения от оси цилиндра (z), угол ориентации проходящей через эту точку и ось плоскости по отношению к некоторой фиксированной плоскости (x0z) и расстояние точки от горизонтальной плоскости (х0у). Заметим, что радиальное направление здесь не совпадает с радиус-вектором. Сферические координаты r, θ, φ (см. рис. 6.3) имеют соответственно следующий смысл: расстояние от начала координат (0), угол ориентации радиального направления по отношению к некоторой оси (z)и угол ориентации плоскости, проходящей через ось и точку наблюдения, по отношению к фиксированной плоскости (x0z).

Основные характеристики цилиндрической и сферической систем сведены в следующую таблицу 6.1.

Орты здесь обозначены теми же буквами, что и соответствующие координаты, и порядок перечисления координат выбран таким, что орты образуют правую тройку векторов; орты угловых координат направлены в сторону возрастания соответствующих углов (рис. 6.6 а, б).

Метрические коэффициенты легко находятся из геометрических соображений (рис. 6.6а, б). Как видно, отвечающие угловым координатам q_i коэффициенты h_i - это просто радиусы окружностей, дугами которых являются элементы длины dl_i.

Таблица 6.1

Номер координаты, i	Система координат коорди* ат
Цилиндрическая ическая	Сферическая
qi		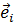hi	dli	qi		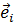hi	dli
	r		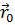1	dr	r		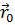1	dr
	α		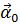r	rdα	θ		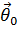r	rdθ
	z		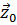1	dz	α		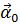rsinθ	rsinθdα

Элемент объема ΔV = Δl₁Δl₂Δl₃ в цилиндрических координатах есть rΔrΔφΔz, а в сферических r²sinθΔrΔθΔφ. Элемент поверхности координатного цилиндра есть rΔφΔz, а координатной сферы r²sinθΔθΔφ.

6.3. Операции векторного анализа в криволинейных ортогональных координатах. На основании общих определений операций векторного анализа нетрудно построить их выражения' в произвольных криволинейных ортогональных координатах.

Градиент. Согласно (2.4) проекции вектора 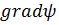на оси криволинейных координат q₁, q₂ и q₃ (т. е. на направления касательных, задаваемые ортами 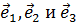имеют вид:

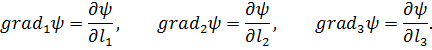
Но ввиду (6.6) 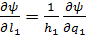и т. д.

Поэтому

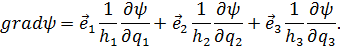
Дивергенция.Вычислим 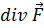в криволинейных координатах подобно тому, как это делалось ранее (п 3.3) в декартовых. Элементарный параллелепипед изображен на рис. 6.7 (ср. рис. 3.5); объём его равен

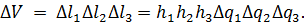
Поток вектора 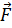через грань 1 и противоположную ей грань 1' вычисляется, как и в п. 3:

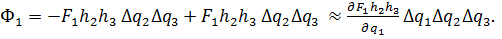
q₁, q₂, q₃ q_1+Δq₁, q₂, q₃

i
Рис. 6.7 Рис. 6.8

(теперь существенно, что не только вектор, но и метрические коэффициенты - функции координат). Аналогичные выражения для потока Ф₂ (грани 2и 2')и потока Ф₃ (грани 3и 3')имеют вид:

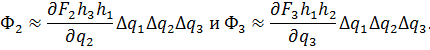
А поскольку

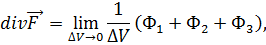
(6.10)

получаем следующее выражение расхождения в криволинейных координатах:

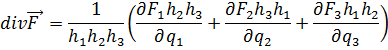
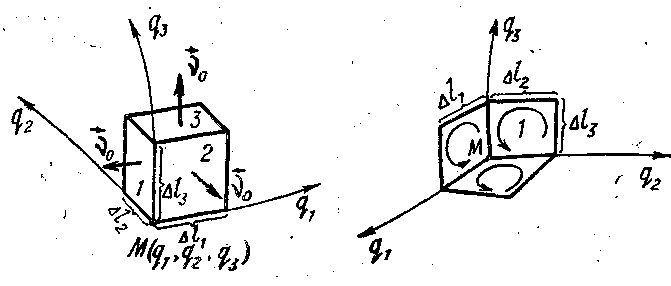
Ротор. Вычисляя в криволинейных координатах rot F, построим рис. 6.8, подобный рис. 4.1. Действуя так же, как и в § 4, п. 2, имеем:

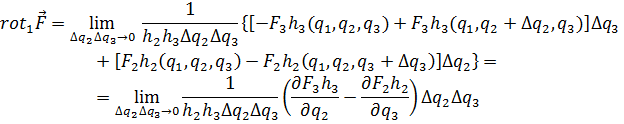
Следовательно,

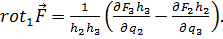(6.11a)

Запишем аналогичные выражения:

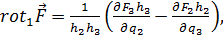(6.11б)

и

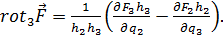(6.11в)

Таким образом, имеем:

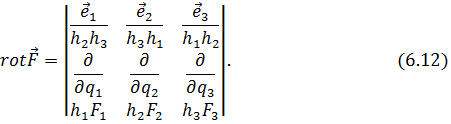
Оператор Лапласа.Формулы (6.10) и (6.9) позволяют записать в криволинейных координатах оператор Лапласа, действующий на скалярную функцию ψ:

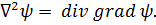
Внося в (6.10)

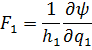
и т. д., получаем:

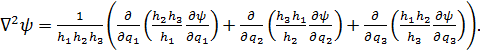(6.13)

При вычислении 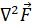(действие на векторную функцию 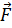)исходят из выражения (5.12):

.

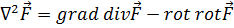Действия в правой части производятся на основании полученных выше выражений (6.9), (6.10), (6.12).

6.4. Операции векторного анализа в цилиндрических и сферических координатах.На основании формул (6.9), (6.10), (6.12) и (6.13) и табл. 6.1 имеем: