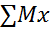Расчёт винтовых цилиндрических пружин с малым шагом витка на прочность. Деформация винтовых цилиндрических пружин.
Расчёт винтовых цилиндрических пружин с малым шагом витка на прочность. Деформация винтовых цилиндрических пружин.
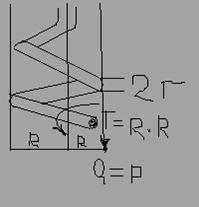Часть 1.Рассмотрим пружину растягиваюмую силами P.
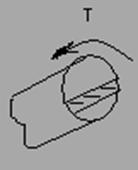Рассечем ее и оставим нижнюю часть.
τ1= Q/A= P/πr2
τ2=T/Wp=2PR/πr3
Wp= πd3/16. τmax=τ1+τ2=P/πr2+2PR/πr3=(2PR/ πr3)(1+r/2R)
r/2R<<1, то можно пренебречь τmax=2PR/ πr3 τmax≤[τ]−условие прочности пружины
Часть 2.
А= 
Pλ U=T2∙L/2G∙Ip
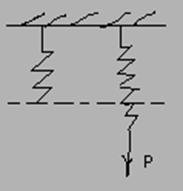U=P2R22πRn/2G Ip= P2R22πRn2/2Gπr4=2 P2R3n/Gr4
L=2πRn
Ip=πdφ/32=πr4/2
Pλ=2 P2R2πRn/Gr4 λ=4 P2R3n/Gr4
20. Типы балок и опор. Плоский поперечный изгиб. Построение эпюр поперечных сил (Q) и изгибающих моментов (М) (пример).Типы балок и опор.
Опоры:1)Шарнирно-подвижная опора
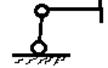2)Шарнирно-неподвижная опора
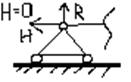3)Заземление или заделка
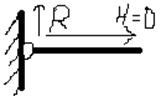Типы балок (стат.-определимых)
1) Консоль 
2)Однопролётная3)Одноконсольная, двухконсольная балка.
4) балки с промежуточным шарниром.
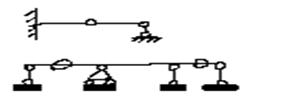
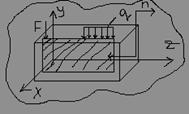Пл. поперечным изгибом наз. такой вид изгиба, когда все силы лежат в одной плоскости перпендикулярно оси бруса, а плоскость их действия совпадает с одной из главных осей инерции.
Qz=∑I
Mz=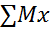 
Построение эпюр в консольной балке.диф зависимости.
Дифференциальные зависимости между нагрузкой (q) поперечной силой (Q) и изгибающим моментом (М).
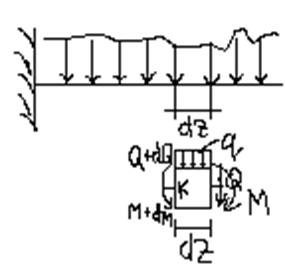∑z = 0
-Q –q∙dz + Q + dQ =0
Q= dQ/dt = tgα
∑mk=0
-M-a∙dz – q∙dz+M+dM=-
Q=dM/dz = tgβ (теорема Журавского)
Q=dQ/dz=d2M/dz2
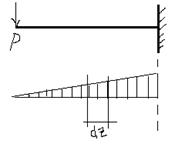
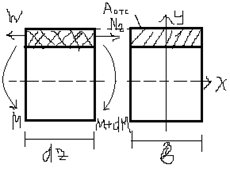23. Определение касательных напряжений при изгибе (формула Журавского)
 |
Эп. «М»
T – сдвигающая сила,∑z = 0;N2-N1-T = 0;N2=Aотс∫Ϭ2∙y∙dA= ((M+dM)S_x^отс)/Ix;
N1= Aотс∫ Ϭ1∙y∙dA = (M∙S_x^отс)/I_x
Будем считать, что кас-е напряжение по площади рассекается равномерно.
T=τ∙A = τ∙dzb; (dM∙S_x^отс)/I_x = τ∙dzb
dM/dz =Qy – теорема Журавского; τ = (d∙M∙S_x^отс)/(I_x∙b∙dz) = (Q∙S_x^отс)/(I_x∙b)
τ = (Q∙S_x^отс)/(I_x∙dy) - формула Журавского; Ix-момент инерции,b-ширина сечения в месте где определяем τ. В поперечном сечении: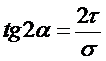 
, 
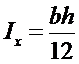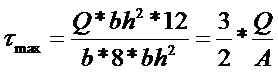
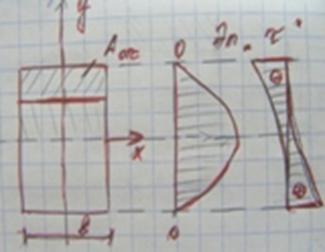
Главные напряжения при изгибе.
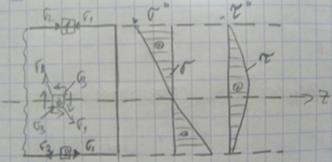Q>0,M>0
, 
, 
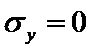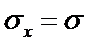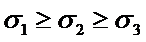
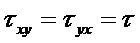
Экстремальное касательное напряжение опр.по формуле: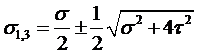 
, две взаимно перпендикулярные наклонные плоскости являются главными плоскостями напряжений в данной точке балки,когда: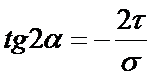 
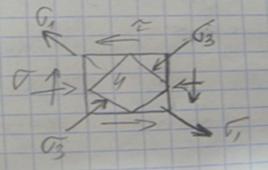
Подбор сечений и проверка прочности балок.
; 
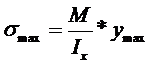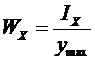-осевой момент сопротивления
; 
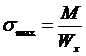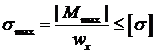-условие прочности при нормальном напряжении
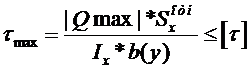
Балки из пластичного материала проверяются на прочность по третьей гипотезе: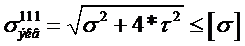 
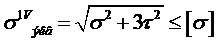подбор сечений производится из условий прочности по нормальным напряжениям.Если в одном и том же поперечном сечении балки одновременно действуют максимальный изгибающий момент и и максимальная поперечная сила или величины Q и М, близкие к максимальным, то в этом сечении производится проверка прочности балки по главным напряжениям.Прочность по главным напряж. Проверяется только для балок,поперечное сечение которых имеет тонкую стенку,резко уширяющуюся вблизи крайних волокон. 
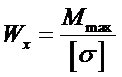-в точках ,где имеет место резкое расширение ширины.
Траектория главн напр.Потенц. энергия при изгибе.
Траектория-линия косат. к каждой точке, которая совпадает с направлением главного движения.
. 
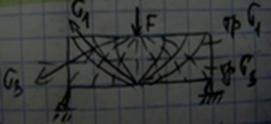
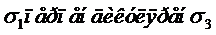
Характер траектории зависит от вида нагрузки и от типа опирания.
Расчёт винтовых цилиндрических пружин с малым шагом витка на прочность. Деформация винтовых цилиндрических пружин.
Часть 1.Рассмотрим пружину растягиваюмую силами P.
Рассечем ее и оставим нижнюю часть.
τ1= Q/A= P/πr2
τ2=T/Wp=2PR/πr3
Wp= πd3/16. τmax=τ1+τ2=P/πr2+2PR/πr3=(2PR/ πr3)(1+r/2R)
r/2R<<1, то можно пренебречь τmax=2PR/ πr3 τmax≤[τ]−условие прочности пружины
Часть 2.
А= Pλ U=T2∙L/2G∙Ip
U=P2R22πRn/2G Ip= P2R22πRn2/2Gπr4=2 P2R3n/Gr4
L=2πRn
Ip=πdφ/32=πr4/2
Pλ=2 P2R2πRn/Gr4 λ=4 P2R3n/Gr4
20. Типы балок и опор. Плоский поперечный изгиб. Построение эпюр поперечных сил (Q) и изгибающих моментов (М) (пример).Типы балок и опор.
Опоры:1)Шарнирно-подвижная опора
2)Шарнирно-неподвижная опора
3)Заземление или заделка
Типы балок (стат.-определимых)
1) Консоль 2)Однопролётная3)Одноконсольная, двухконсольная балка.
4) балки с промежуточным шарниром.
Пл. поперечным изгибом наз. такой вид изгиба, когда все силы лежат в одной плоскости перпендикулярно оси бруса, а плоскость их действия совпадает с одной из главных осей инерции.
Qz=∑I
Mz=