Задача № 3 Расчет на прочность и жесткость балки при поперечном ударе

На упругую балку заданного поперечного сечения с высоты Н свободно падает

абсолютно жесткое тело массой m. Определить допустимую величину массы падающего тела 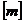, при которой будет обеспечена прочность балки, приняв 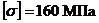. Проверить выполнение условия жесткости, приняв 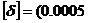- 0.001)L, где L – расстояние между опорами. Массой балки пренебречь.

План решения

1. Исходную балку статически нагрузить силой, равной по величине весу падающего тела, приложенной в точке удара и действующей в направлении удара.

2. Для полученной таким образом схемы выполнить статический расчет (в долях массы m):

– определить статическое перемещение 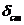в точке удара в направлении его действия;

– найти максимальное статическое напряжение ;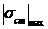

– найти максимальный статический прогиб .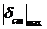

3. Определить динамический коэффициент (в долях массы m).

4. Записать условие прочности при ударе, из которого подобрать допускаемую величину массы падающего тела .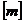

5. Определить максимальный динамический прогиб балки при m= 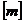и проверить выполнение условия жесткости.

Примечание.Вариант задания выбирается по схеме:

1-я цифра варианта – номер схемы балки (рис.3.1)

2-я цифра варианта – номер поперечного сечения (рис. 3.2)

3-я цифра варианта – номер строки числовых данных (табл. 6.3)

Таблица 3

№ вар.	l, м	k	H, м	b, м	k1	Двутавр, швеллер №	Уголок неравнобокий №	Уголок равнобокий №
	1,0	0,20	1,2		0,22		5/3,2
	1,2	0,80	1,3		0,32		7,5/5	5,6
	1,5	0,30	1,0		0,24		9/5,6	6,3
	1,3	0,40	1,4		0,34		5/3,2
	1,4	0,70	1,1		0,26		7,5/5	7,5
	1,6	0,45	1,5		0,36		9/5,6
	1,7	0,50	1,2		0,28		10/6,3
	1,9	0,65	1,6		0,38		11/7
	1,8	0,55	1,1		0,20		10/6,3
	2,0	0,60	2,0		0,30		11/7	12,5

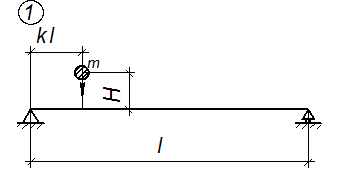
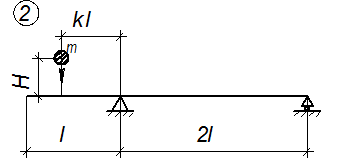
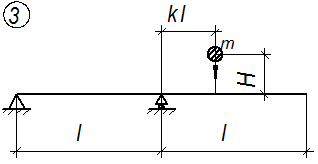
Расчетные схемы балок к задаче № 3

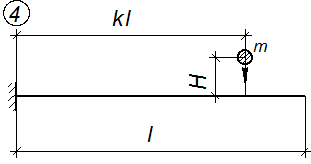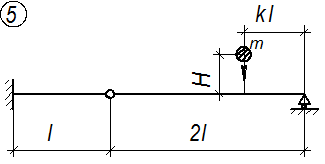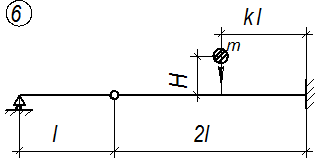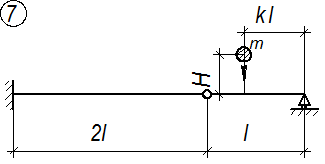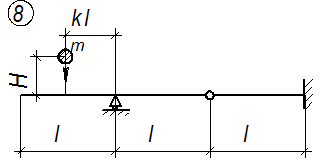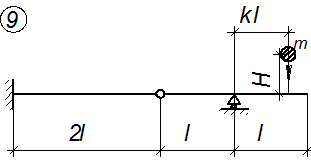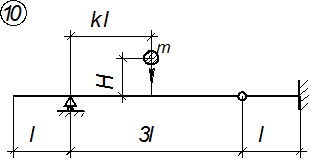Рис. 3.1.

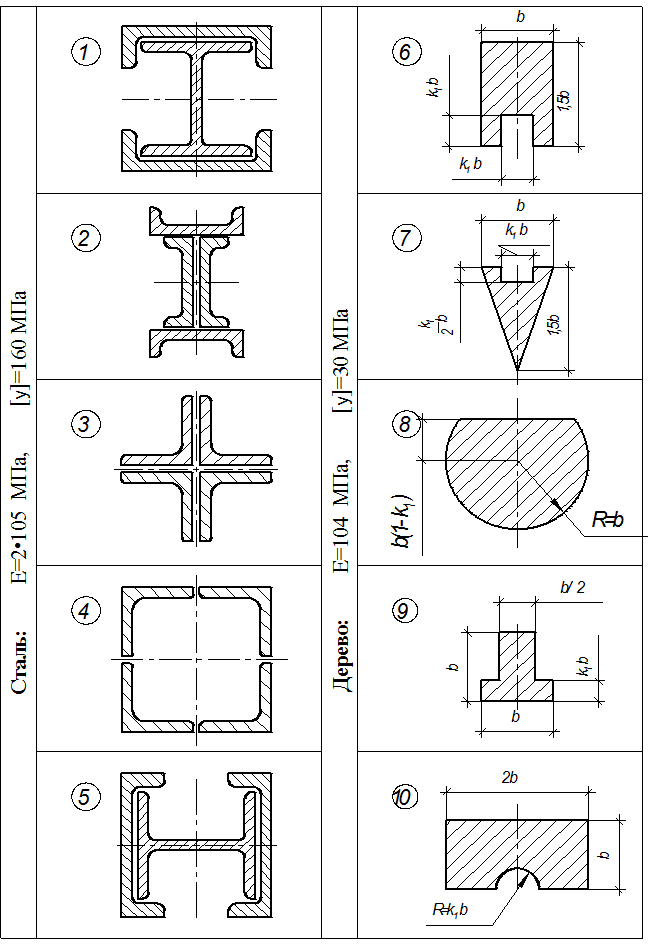Рис. 3.2

Вопросы для подготовки к экзамену

Сложное сопротивление

1. Чем отличается косой изгиб от прямого изгиба?

2. Для каких форм поперечных сечений случай косого изгиба невозможен?

3. Отличительная особенность расчета напряжений для случая косого изгиба.

4. Отличительная особенность расчета напряжений для случая совместного действия прямого изгиба с растяжением-сжатием.

5. Отличительная особенность расчета напряжений для случая совместного действия косого изгиба с растяжением-сжатием.

6. Анализ положения опасных точек в опасном сечении прямоугольного профиля для общего случая сложного сопротивления (в сечении присутствуют все 6 ВСФ)

Напряженное состояние в точке и теории предельного состояния

1. Какие типы напряженных состояний Вы знаете?

2. Что такое главное напряжение?

3. Каково соотношение между главными напряжениями?

4. По какому принципу делятся все теории предельного состояния?

5. В чем особенность теории Мора?

6. Какой критерий лежит в основе 3 теории предельного состояния?

7. Какой критерий лежит в основе 4 теории предельного состояния?