Вынужденные колебания упругой системы с одной степенью свободы

Добавим к числу сил, действующих на систему, вынуждающую силу F₀sinWt, где W - частота вынуждающей силы:

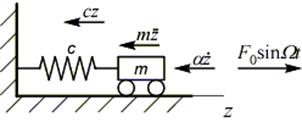
При этом уравнение равновесия принимает вид

.

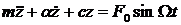Введем обозначение .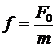

Таким образом, дифференциальное уравнение, описывающее вынужденные колебания упругой системы с одной степенью свободы с учетом сил сопротивления имеет вид:

.

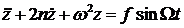Примем частное решение данного дифференциального уравнения в виде 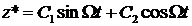. Его первая и вторая производная имеют вид

,

.

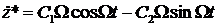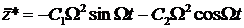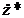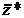Подставляя выражения для и в дифференциальное уравнение, получим

.

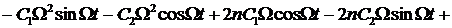
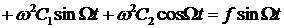
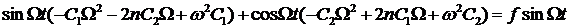Данное равенство будет выполняться, если

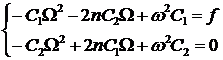
Из последнего уравнения выразим С₂:

,

.

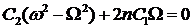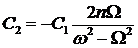Преобразуем первое уравнение:

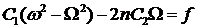
и подставим в него выражение для C₂:

,

.

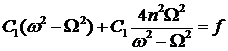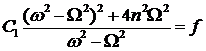Таким образом, коэффициенты уравнения колебательного процесса принимают вид:

; .

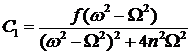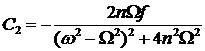Введем обозначения:

,

.

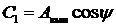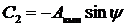С учетом этих обозначений уравнение вынужденных колебаний можно записать в виде:

.

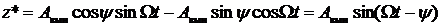Отсюда видно, что A_вын – амплитуда вынужденных колебаний, y – фазовый сдвиг между вынуждающей силой и вызываемыми ею колебаниями.

Определим амплитуду вынужденных колебаний:

,

,

.

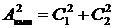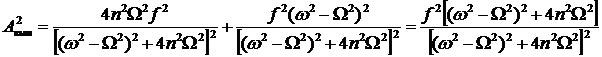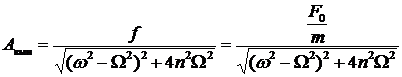Выразим массу из формулы для частоты собственных колебаний:

→ .

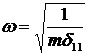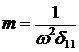Тогда амплитуда вынужденных колебаний вычисляется по следующей формуле:

.

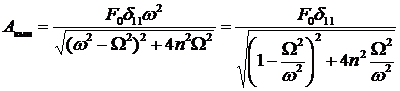Здесь 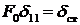– статическое перемещение точки, за колебанием которой мы наблюдаем. То есть, если амплитудную величину возмущающей силы приложить к данной точке статически (в направлении колебательного процесса), то эта точка получит статическое перемещение .

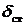Тогда представим формулу для амплитуды вынужденных колебаний в следующем виде:

,

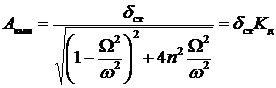где 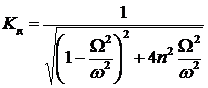- коэффициент динамичности.

Таким образом, амплитуда вынужденных колебаний (динамическое перемещение):

.

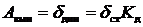В соответствии с законом Гука напряжение прямо пропорционально деформации, то есть

.

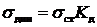Если 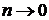либо 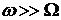, то коэффициент динамичности

.

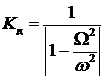График зависимости коэффициента динамичности от отношения частот вынужденных и собственных колебаний:

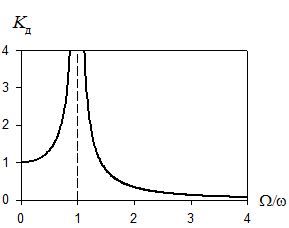
При 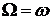: 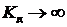– это случай резонанса.

Фазовый сдвиг:

.

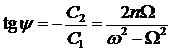При 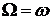фазовый сдвиг 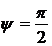, т.е. вынуждающая сила достигает максимального значения в момент, когда колебательная система проходит через состояние равновесия. Это и является причиной резонанса.

Удар

Ударом называется взаимодействие тел, при котором силы взаимодействия резко нарастают или ослабевают за короткий промежуток времени. Удар относится к динамическим видам нагружения.

Можно выделить три вида задач об ударе:

1. Задачи об изменении параметров движения взаимодействующих тел, решаемые аппаратом механики недеформируемого твердого тела.

2. Задачи о напряжениях и деформациях, возникающих во взаимодействующих телах, решаемые аппаратом механики деформируемого твердого тела.

3. Задачи об определении свойств материалов при ударе.

В курсе «Сопротивление материалов» решаются ударные задачи только второго вида: производится расчет на прочность и жесткость элементов конструкций при ударном нагружении. Более общий подход к решению таких задач был предложен доктором технических наук, основателем кафедры «Сопротивление материалов» Тольяттинского политехнического института Георгием Федоровичем Лепиным.

Теория удара Лепина

Основные допущения:

1. Ударяющее тело абсолютно жесткое.

2. Материал ударяемого тела следует закону Гука.

3. Ударяемое тело имеет одну степень свободы.

4. Удар неупругий, т.е. ударяющее тело после удара не отскакивает, а движется совместно с ударяемым телом.

5. Кинетическая энергия ударяющего тела полностью переходит в потенциальную энергию деформации ударяемого тела, т.е. можно пренебречь контактными явлениями.

6. Деформация мгновенно распространяется по ударяемой системе, и все ее точки начинают движение одновременно, т.е. можно пренебречь волновыми явлениями.

Рассмотрим упругую систему в виде пружины длиной l и жесткостью c с грузом весом F₁. Пружина образует с горизонтом угол a и под действием веса груза имеет деформацию d. Абсолютно жесткое тело весом F движется со скоростью v под углом b к горизонту.

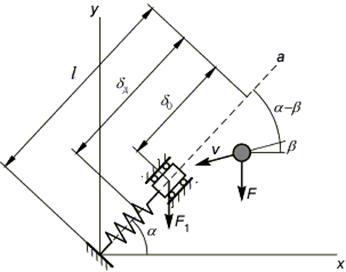
Определим перемещение упругой системы d_д после удара (динамическое перемещение).

В соответствии с законом сохранения импульса, количество движения системы до и после удара одинаково. Проецируя количество движения на ось a, можно записать:

,

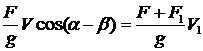где V₁ – скорость движения системы после соударения:

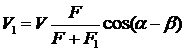. (4.1)

Воспользуемся теоремой о кинетической энергии:

T₂ – T₁ = I, (4.2)

где T₁, T₂ – кинетическая энергия в начале и конце ударного взаимодействия соответственно, I - работа всех сил на перемещении во время ударного взаимодействия.

Кинетическая энергия системы в начале взаимодействия равна

.

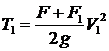Подставляя сюда вместо V₁ выражение (11.1), получим:

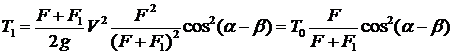, (4.3)

где 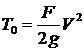– кинетическая энергия ударяющего тела.

В конце ударного взаимодействия система неподвижна, и ее кинетическая энергия T₂=0.

Работа внешних сил складывается из работы силы тяжести и силы упругости пружины:

.

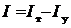Работа силы тяжести системы на перемещении, вызванном ударом:

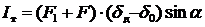. (4.4)

Рассмотрим зависимость силы упругости F_у от перемещения d. По закону Гука :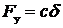

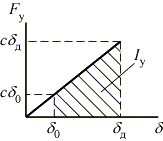
Как видно из графика, работа силы упругости на перемещении, вызванном ударом, определяется

.

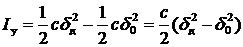Представим жесткость пружины в виде 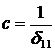, где d₁₁ – податливость упругой системы (перемещение точки соударения под действием единичной силы, приложенной по направлению перемещения во время ударного взаимодействия). Тогда работа сил упругости

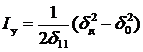. (4.5)

Формула (11.2) с учетом выражений (11.3), (11.4) и (11.5) принимает вид:

,

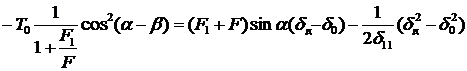откуда

,

,

.

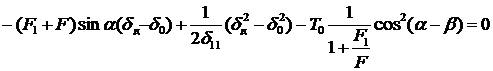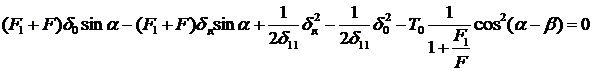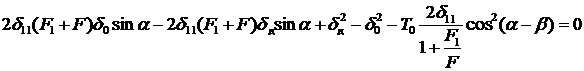Учитывая, что 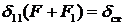– статическое перемещение (перемещение точки соударения под действием силы тяжести взаимодействующих тел, приложенной статически по направлению перемещения во время ударного взаимодействия):

.

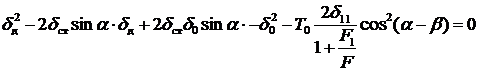Поскольку корни квадратного уравнения вида 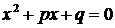равны 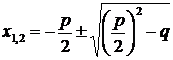, то

,

.

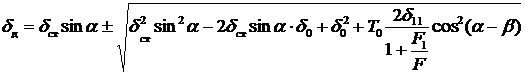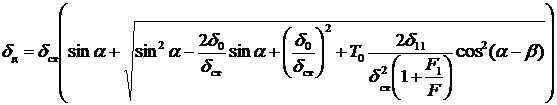Таким образом, перемещение при ударе вычисляется по формуле:

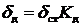, (4.6)

где K_д – коэффициент динамичности:

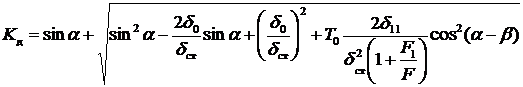(4.7)

В области упругих деформаций напряжение, возникающее при ударе

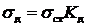. (4.8)

Частные случаи удара

1. Тело массой m падает на упругую систему массой m₁ с высоты H.

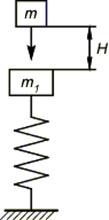
В данном случае

a=b=90°,

,

,

.

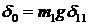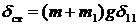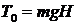Коэффициент динамичности:

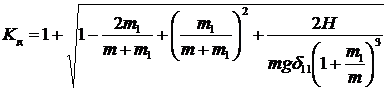(4.9)

2. Тело массой m падает на невесомую упругую систему с высоты H.

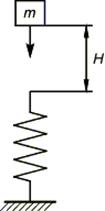
Из предыдущего пункта коэффициент динамичности при m₁ = 0:

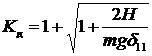. (4.10)

В случае, когда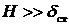

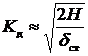. (4.11)

3.Мгновенное приложение нагрузки.

Из предыдущего пункта коэффициент динамичности при H = 0:

K_д = 2. (4.12)

4.Тело массой m равномерно спускалось со скоростью V до момента заклинивания троса в обойме блока.

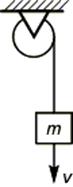
В данном случае

a=b=90°,

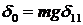(пренебрегаем массой троса),

,

.

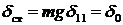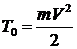Коэффициент динамичности:

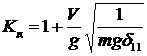. (4.13)

5. Тело массой m свободно падало до момента заклинивания троса в обойме блока, достигнув к этому времени скорости V.

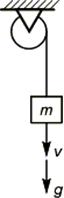
В данном случае

a=b=90°,

,

,

.

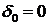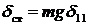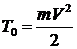Коэффициент динамичности:

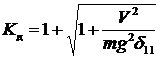. (4.14)

1. Горизонтальный удар.

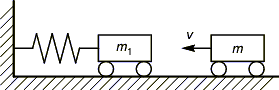
В данном случае

a=b=0°,

,

,

.

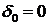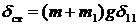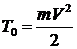Коэффициент динамичности:

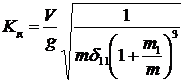. (4.15)

7. Горизонтальный удар по системе, массой которой можно пренебречь.

Из предыдущего пункта коэффициент динамичности при m₁ = 0:

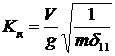. (4.16)