Сингулярные и линейно-сингулярные процессы

В задачах автоматизированного и автоматического управления широкое применение находят так называемые вырожденные процессы, которые можно определить по следующей схеме. Пусть вектор-столбец Х есть n-мерный случайный вектор. Распределение вектора Х называется сингулярным, или, более точно, линейно-сингулярным, если существует n-мерный вектор А, такой, что вероятность

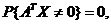
или, иными словами, если случайная величина 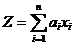, где 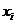-компоненты вектора Ч, с вероятностью 1 при любых 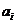равна нулю.

Определение 1.7.

Случайный процесс 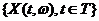называется сингулярным (линейно-сингулярным), если существует случайный оператор L такой, что вероятность

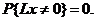
Простым примером сингулярного процесса является процесс

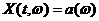для всех t, где a-случайная переменная.

Более сложным примером является процесс

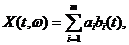
где 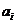-случайные переменные, а 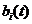-известные неслучайные функции времени.

Сингулярные процессы широко используются в задачах имитационного моделирования вероятностных систем, где с помощью их приближаются реальные процессы.

Процессы с независимыми приращениями

Определение 1.8.

Случайный процесс 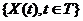называется процессом с независимыми или ортогональными приращениями, если случайные величины

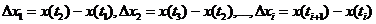взаимно независимы.

Процесс с независимыми приращениями определяется распределением случайной величины 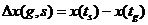для произвольных s, g и распределением 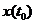. Если распределение 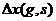зависит только от (s-g),то 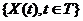называется процессом со стационарными приращениями. Если 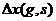имеет нормальное распределение, то 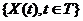называется процессом с независимыми нормальными приращениями.

Особенно интересным является винеровский процесс, или процесс броуновского движения [2]. Он имеет большое значение для разработки теории случайных процессов. Типичная выборочная функция этого процесса представлена на рис.2.

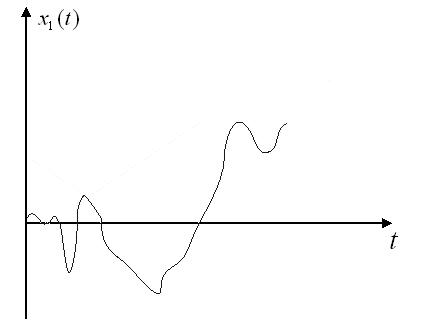
Рис. 2. Выборочная функция винеровского процесса

Винеровский процесс определен для 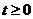и обладает следующими свойствами:

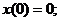
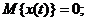
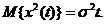(1.11)

Плотность вероятности x(t) имеет вид

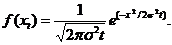
Поскольку винеровский процесс нормальный, он характеризуется полностью математическим ожиданием и корреляционной функцией, имеющих следующий вид:

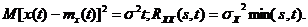
Марковские процессы

Определение 1.9.

Случайный процесс 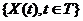называется Марковским процессом, если условные вероятности удовлетворяют равенству

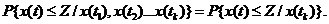(1.12)

Равенство (1.12) означает, что для прогнозирования значения 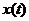нет необходимости знать всю предысторию процесса. Достаточно знать лишь значение .

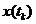Функция распределения величины 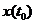называется начальной функцией распределения. Функция

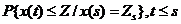(1.13)

называется функцией распределения вероятностей перехода.

Пусть 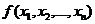- плотность вероятности случайных величин 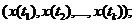используя свойство (1.12), её можно записать в виде

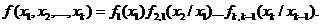(1.14)

применяя формулу полной вероятноcти [1], выражение (1.14) можно привести к виду

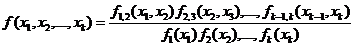(1.15)

Если 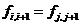, то Марковский процесс полностью определяется двумя функциями: функцией распределения и вероятностью перехода (1.12).

Марковские случайные процессы, особенно с дискретными значениями 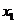, являются исключительно важными для вероятностных задач анализа и синтеза АСУ. Они подробно будут рассмотрены в раз. 2.