В.2 Матрицы и операции над ними
В.1 Определители, их свойства и вычисление
Каждой квадратной матрице A порядка n можно поставить в соответствие единственное число, которое вычисляется по определенному правилу. Это число называется определителем (или детерминантом) матрицы A и обозначается |A|, или det A, или Δ(A). Порядок матрицы A является и порядком ее определителя. Определители порядка 1-3 определяются, соответственно, равенствами:
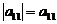 ,
,
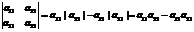 , (3)
, (3)
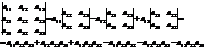 .
.
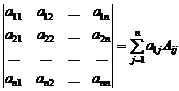
Минором Mij элемента aij , 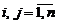 , называется определитель (n-1)-го порядка, который состоит из элементов матрицы, полученной из данной после «вычеркивания» i- той строки и j-того столбца.
, называется определитель (n-1)-го порядка, который состоит из элементов матрицы, полученной из данной после «вычеркивания» i- той строки и j-того столбца.
Алгебраическим дополнением элемента aijназываетсячисло Аij=(-1)i+jMij.Определитель порядка n, где 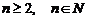
 , определяется как число.
, определяется как число.
Последнее равенство называют разложением определителя по элементам первой строки. Оно есть обобщение равенств (3).
Свойства определителей:
1) 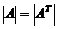 ;
;
2) 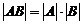 ;
;
3) общий множитель элементов какой-либо строки (столбца) можно вынести за знак определителя;
4) перестановка двух строк (столбцов) меняет знак определителя на противоположный;
5) |A|=0, если выполняется одно из следующих условий:
· в определителе есть нулевая строка (нулевой столбец),
· в определителе есть пропорциональные строки (столбцы),
· в определителе есть строки (столбцы), являющиеся линейной комбинацией соответствующих элементов других строк (столбцов);
6) если к элементам одной строки (столбца) определителя прибавить линейную комбинацию соответствующих элементов других строк (столбцов), то значение определителя не изменится.
Основные методы вычисления определителей.
1. Для определителей 3-го порядка удобно использовать правило треугольников, которое схематично можно изобразить следующим образом:
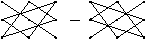
Линии соединяют по три элемента, которые умножаются, а затем произведения складываются.
2. Определитель порядка n может быть вычислен разложением по любой строке (столбцу):
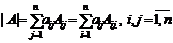 .
.
3. Метод эффективного понижения порядка определителя: используя свойства определителя, его преобразуют к такому виду, чтобы все элементы некоторой строки (столбца) определителя, кроме одного, были нулями, затем вычисляют определитель разложением по этой строке (столбцу).
4. Метод приведения к треугольному или диагональному виду с использованием свойств определителя, когда определитель равен произведению диагональных элементов.
.
Метод окаймляющих миноров
Если в матрице A найден ненулевой минор Mk порядка k, 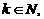 а все окаймляющие его миноры
а все окаймляющие его миноры 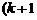 )-го порядка равны нулю, то ранг матрицы равен k (
)-го порядка равны нулю, то ранг матрицы равен k ( 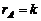 ).
).
Метод элементарных преобразований
Используя элементарные преобразования строк, матрицу приводят к трапециевидной или треугольной форме, далее ранг находят по определению.
Как частный случай последнего метода, может быть рассмотрен метод нулей и единиц: элементарными преобразованиями строк матрицу приводят к эквивалентной, состоящей или из нулевых строк и столбцов, или из строк и столбцов, в которых содержится ровно одна единица, а остальные элементы – нулевые. Количество единиц в такой матрице равно ее рангу.
В.10 Векторное произведение
Векторным произведением 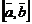 двух векторов
двух векторов 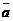 и
и 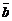 называется вектор, удовлетворяющий следующим условиям:
называется вектор, удовлетворяющий следующим условиям:
1) 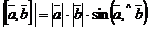 ;
;
2) 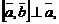
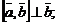
3) тройка векторов 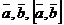 – правая.
– правая.
Векторное произведение обозначают также 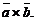
Если хотя бы один из векторов 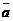 или
или 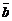 нулевой, то
нулевой, то 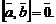
Геометрический смысл векторного произведения 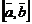 состоит в том, что длина этого вектора численно равна площади параллелограмма, построенного на векторах
состоит в том, что длина этого вектора численно равна площади параллелограмма, построенного на векторах 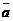 и
и 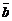 :
:
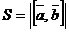 .
.
Физический смысл векторного произведения состоит в том, что момент 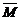 силы
силы 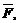 приложенной к точке A, относительно точки O есть векторное произведение векторов
приложенной к точке A, относительно точки O есть векторное произведение векторов 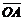 и
и 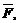 т. е.
т. е.
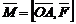 .
.
Свойства векторного произведения:
1) 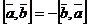 ;
;
2) 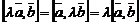 ;
;
3) 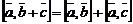 ;
;
4) 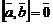 при
при 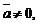
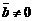 тогда и только тогда, когда векторы
тогда и только тогда, когда векторы 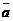 и
и 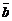 коллинеарны.
коллинеарны.
Если 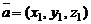 и
и 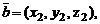 то
то
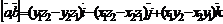
Последнюю формулу удобно записать в виде формального определения третьего порядка:
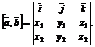
Плоскость в пространстве
1. Положение плоскости P в пространстве относительно прямоугольной системы координат Oxyz однозначно определено, если задан радиус-вектор 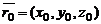 некоторой фиксированной точки
некоторой фиксированной точки 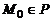 и два некомпланарных вектора
и два некомпланарных вектора 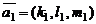 и
и 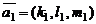 , параллельных данной плоскости. В этом случае равенство
, параллельных данной плоскости. В этом случае равенство 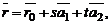 где
где 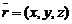 – радиус-вектор произвольной точки
– радиус-вектор произвольной точки 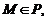
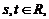 называется векторно-параметрическим уравнением плоскости P. Записав его в координатной форме получим параметрические уравнения плоскости.
называется векторно-параметрическим уравнением плоскости P. Записав его в координатной форме получим параметрические уравнения плоскости.
2. Эту же плоскость можно задать одним из уравнений:
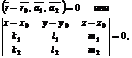 (1)
(1)
справедливость которых обусловлена условием компланарности векторов 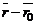 ,
, 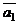 и
и 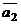 .
.
3. Координаты векторов 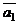 и
и 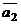 могут быть найдены, если известны три точки плоскости P, не лежащие на одной прямой:
могут быть найдены, если известны три точки плоскости P, не лежащие на одной прямой: 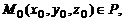
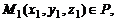
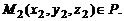
В этом случае 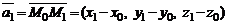 ,
, 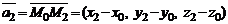 . В результате имеем уравнение плоскости, проходящей через три заданные точки, не лежащие на одной прямой.
. В результате имеем уравнение плоскости, проходящей через три заданные точки, не лежащие на одной прямой.
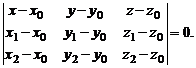
4. Если известны точки пересечения плоскости P с координатными осями, т. е. M0(a, 0, 0), M1(0, b, 0), M2(0, 0, c), то справедливо уравнение «в отрезках»:
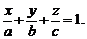
5. Положение плоскости P в пространстве однозначно определено и в том случае, когда задан нулевой нормальный вектор 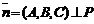 и точка
и точка 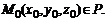 Условия перпендикулярности векторов
Условия перпендикулярности векторов 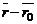 и
и 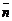 позволят перейти к векторному уравнению
позволят перейти к векторному уравнению 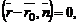 а затем к его координатной форме записи:
а затем к его координатной форме записи:
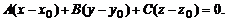 (2)
(2)
После преобразования последнего уравнения приходим к общему уравнению плоскости P:
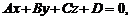 где
где 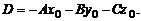
6. Если в качестве нормального вектора плоскости P взять единичный вектор 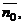 направленный из начала координат в сторону плоскости, то
направленный из начала координат в сторону плоскости, то 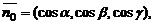 где
где 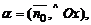
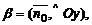
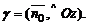 Тогда справедливо нормальное уравнение плоскости
Тогда справедливо нормальное уравнение плоскости
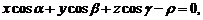
где 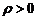 – расстояние от начала координат до плоскости.
– расстояние от начала координат до плоскости.
Величина 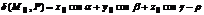 , где
, где 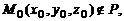 называется отклонением точки
называется отклонением точки 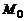 от плоскости
от плоскости 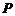 . При этом
. При этом 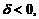 если
если 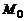 и O(0, 0, 0) лежат по одну сторону от плоскости,
и O(0, 0, 0) лежат по одну сторону от плоскости, 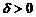 – если лежат по разные,
– если лежат по разные, 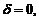 если
если 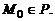 Расстояние
Расстояние 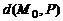 от точки
от точки 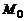 до плоскости
до плоскости 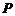 равно абсолютному значению ее отклонения, т. е.
равно абсолютному значению ее отклонения, т. е.
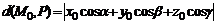 .От общего уравнения плоскости к нормальному можно перейти с помощью умножения на нормирующий множитель
.От общего уравнения плоскости к нормальному можно перейти с помощью умножения на нормирующий множитель
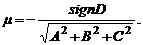
Значит, расстояние 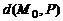 от точки
от точки 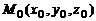 до плоскости
до плоскости 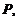 заданной общим уравнением
заданной общим уравнением 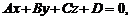 может быть найдено по формуле
может быть найдено по формуле
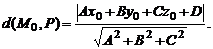
Угол 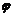 между плоскостями в пространстве определяется по косинусу угла между нормальными векторами
между плоскостями в пространстве определяется по косинусу угла между нормальными векторами 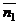 и
и 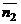 этих плоскостей:
этих плоскостей:
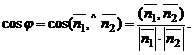
Расположение прямых
Положение прямой в пространстве относительно прямоугольной системы координат однозначно определено, если известны координаты ее направляющего вектора 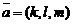 и некоторой фиксированной точки
и некоторой фиксированной точки 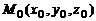 этой прямой. Тогда радиус-вектор
этой прямой. Тогда радиус-вектор 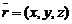 произвольной точки M, лежащей на прямой, может быть представлен в виде
произвольной точки M, лежащей на прямой, может быть представлен в виде
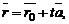
где 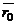 – радиус-вектор точки
– радиус-вектор точки 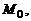
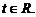 Полученное веккторно-параметрическое уравнение в координатной форме равносильно трем параметрическим уравнениям:
Полученное веккторно-параметрическое уравнение в координатной форме равносильно трем параметрическим уравнениям:
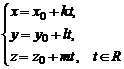
Исключая параметр t, придем к параметрическим уравнениям:
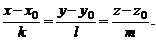
Прямую в пространстве можно задать и как линию пересечения двух плоскостей, заданных общими уравнениями, т. е. системой линейных уравнений:
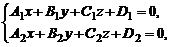
где коэффициенты при неизвестных не являются пропорциональными.
Расстояние 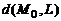 от точки
от точки 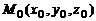 до прямой L с направляющим вектором
до прямой L с направляющим вектором 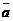 и проходящей через точку
и проходящей через точку 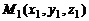 может быть найдено по формуле
может быть найдено по формуле
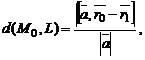
где 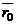 и
и 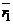 – радиус-векторы точек
– радиус-векторы точек 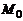 и
и 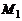 соответственно.
соответственно.
Эту формулу можно использовать и для нахождения расстояния между параллельными прямыми.
Если прямые 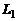 и
и 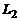 являются скрещивающимися, то расстояние между ними
являются скрещивающимися, то расстояние между ними
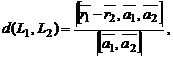
где 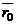 и
и 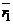 – радиус-векторы точек
– радиус-векторы точек 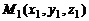 и
и 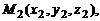 принадлежащих прямым
принадлежащих прямым 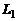 и
и 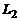 соответственно, а векторы
соответственно, а векторы 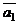 и
и 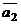 – их направляющие векторы.
– их направляющие векторы.
О взаимном расположении двух прямых в пространстве можно судить по их направляющим векторам.
Прямые параллельны при условии коллинеарности их направляющих векторов (координаты пропорциональны).
Прямые перпендикулярны при условии перпендикулярности их направляющих векторов (скалярное произведение равно 0).
Угол между прямыми можно определить через косинус угла между направляющими векторами.
Прямые лежат в одной плоскости при условии компланарности их направляющих векторов и вектора 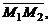 где
где 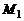 и
и 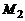 – точки этих прямых (смешанное произведение равно 0).
– точки этих прямых (смешанное произведение равно 0).
Расстояние от точки 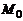 до прямой L
до прямой L
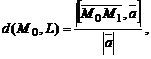
где 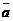 – направляющий вектор,
– направляющий вектор, 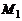 – точка прямой.
– точка прямой.
Поверхности второго порядка
Алгебраической поверхностью второго порядка называется поверхность S, общее уравнение которой в декартовой прямоугольной системе координат относительно текущих координат 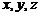 имеет вид
имеет вид
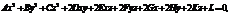 где коэффициенты при одночленах второй степени одновременно не равны нулю.
где коэффициенты при одночленах второй степени одновременно не равны нулю.
Эти уравнения определяют тип поверхности и называются каноническими.
1. Эллипсоид: 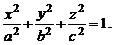
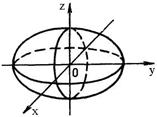
2. Гиперболоид
1) эллиптический: 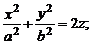 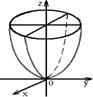 | 2) гиперболический: 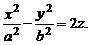 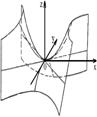 |
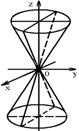
3. Конус второго порядка: 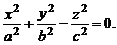
4. Параболоид
5. Цилиндр
1) эллиптический: 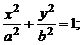 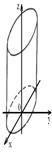 | 2) гиперболический: 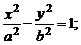 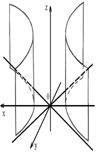 |
3) параболический: 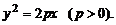
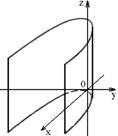
Основным методом исследования формы поверхности является метод сечений, который состоит в следующем. Поверхность пересекается координатными плоскостями и им параллельными, а затем на основании вида полученных в сечениях линий делается вывод о виде поверхности. Таким образом изучаются основные геометрические свойства невырожденных поверхностей второго порядка на основе их канонических уравнений.
При этом, когда в общем уравнении поверхности коэффициенты 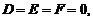 приведение к каноническому виду осуществляется с помощью метода выделения полных квадратов и параллельного переноса системы координат. При наличии же в общем уравнении поверхности смешанных произведений переменных приведение к каноническому виду опирается на теорию квадратичных форм.
приведение к каноническому виду осуществляется с помощью метода выделения полных квадратов и параллельного переноса системы координат. При наличии же в общем уравнении поверхности смешанных произведений переменных приведение к каноническому виду опирается на теорию квадратичных форм.
В любом случае, общее уравнение поверхности может быть приведено к уравнениям, задающим так называемые вырожденные поверхности. Приведем примеры таких случаев.
1. 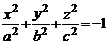 – пустое множество точек (мнимый эллипсоид);
– пустое множество точек (мнимый эллипсоид);
2. 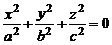 – точка (0, 0, 0);
– точка (0, 0, 0);
3. 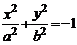 – пустое множество точек
– пустое множество точек
Определение по Коши
Число А называется пределом функции f(x) в точке х0, если функция определена в некоторой выколотой окрестности точки х0 и если для любого сколь угодно малого числа 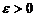 существует такое число
существует такое число 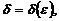 что для всех х, удовлетворяющих условию
что для всех х, удовлетворяющих условию
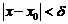 (1)
(1)
выполняется
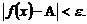 (2)
(2)
Это записывают:
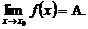
Число А называется пределом функции на бесконечности, если для любого 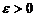 существует число
существует число 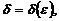 что для всех х, удовлетворяющих условию
что для всех х, удовлетворяющих условию
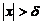
выполняется неравенство
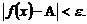
Это записывают:
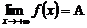 (
( 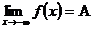 ).
).
Определение предела функции в точке (на бесконечности) по Гейне и по Коши эквивалентны.
Функция f(x) называется бесконечно большой при 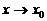
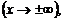 если для всякого числа М > 0 существует
если для всякого числа М > 0 существует 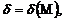 что для всех х, удовлетворяющих условию
что для всех х, удовлетворяющих условию
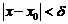 (
( 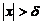 )
)
выполняется неравенство
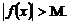
Это записывают:
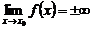
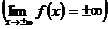 .
.
Если f(x) – бесконечно большая функция при 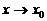
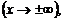 то она не имеет предела в этой точке (на бесконечности). Символ предела в данном случае используют лишь для обозначения.
то она не имеет предела в этой точке (на бесконечности). Символ предела в данном случае используют лишь для обозначения.
Функция f(x) называется бесконечно малой при 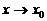
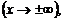 если
если
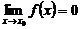
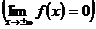 .
.
Замечательные пределы
При вычислении пределов в случае неопределенностей часто используют специальные формулы, которые называются замечательными пределами.
Второй замечательный предел
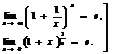 (8)
(8)
Третий замечательный предел
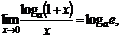 (9)
(9)
в частности,
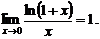
Пятый замечательный предел
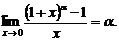 (11)
(11)
Указанные формулы (7)–(11) замечательных пределов обобщаются на любую функцию u(x), стоящую вместо независимой переменной х при условии, что 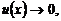 если
если 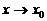 (или
(или 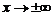 ) во всех формулах кроме (8), в которых
) во всех формулах кроме (8), в которых 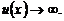
Обобщенная таблица замечательных пределов
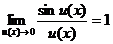 ;
;
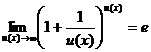 ;
; 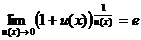 ; (12)
; (12)
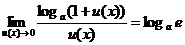 ;
; 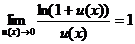 ; (13)
; (13)
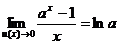 ;
; 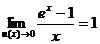 ; (14)
; (14)
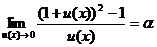 . (15)
. (15)
При использовании обобщенных форму на практике вместо 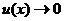
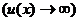 (под знаком предела пишут указанное в условии:
(под знаком предела пишут указанное в условии: 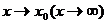 .
.
Все приведенные формулы обобщенной таблицы замечательных пределов (кроме формул (12)) раскрывают неопределенность типа 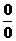 . Формулы (12) раскрывают неопределенность типа
. Формулы (12) раскрывают неопределенность типа 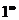 .
.
Эквивалентность функции
Две функции 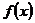 и
и 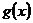 называются эквивалентными бесконечно малыми, при
называются эквивалентными бесконечно малыми, при 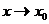
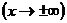 , если
, если
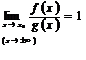 ,
,
это записывают 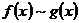 при
при 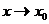
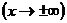 .
.
При вычислении пределов функций в точке и на бесконечности удобно пользоваться следующей теоремой:
Если 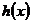 ,
, 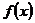 и
и 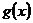 - некоторые функции, определенные в
- некоторые функции, определенные в
окрестности точки 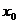 (на числовой полуоси) и
(на числовой полуоси) и 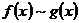 при
при
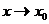
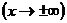 , то
, то
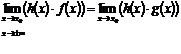 . (16)
. (16)
Формула (16) показывает, что в произведении можно заменять функцию – сомножитель на эквивалентную ей – более простую для вычисления предела.
Таблица эквивалентных бесконечно малых
Пусть 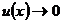 , если
, если 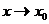
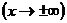 . Тогда справедливы следующие эквивалентности:
. Тогда справедливы следующие эквивалентности:
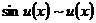 ; (17)
; (17)
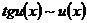 ; (18)
; (18)
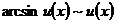 ; (19)
; (19)
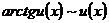 ; (20)
; (20)
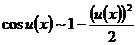 ; (21)
; (21)
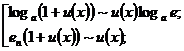 (22)
(22)
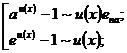 (23)
(23)
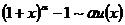 (24)
(24)
Точек разрыва.
Функция 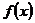 называется непрерывной в точке
называется непрерывной в точке 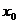 , если она определена в этой точке в некоторой ее окрестности и
, если она определена в этой точке в некоторой ее окрестности и
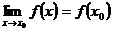 (27)
(27)
Если функция 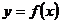 непрерывна в каждой точке некоторого промежутка, то говорят, что функция непрерывна на этом промежутке.
непрерывна в каждой точке некоторого промежутка, то говорят, что функция непрерывна на этом промежутке.
Существуют и другие определения непрерывности функции в точке. Функция 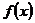 называется непрерывной в точке , если она определена в этой точке и в некоторой ее окрестности и если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции в этой точке:
называется непрерывной в точке , если она определена в этой точке и в некоторой ее окрестности и если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции в этой точке:
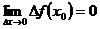 (28)
(28)
Непрерывность функции в точке определяется также на основе односторонних предметов.
Функция 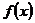 называется непрерывной в точке
называется непрерывной в точке 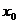 , если она определена в этой точке и некоторой ее окрестности и существует односторонние пределы (конечные) такие, что
, если она определена в этой точке и некоторой ее окрестности и существует односторонние пределы (конечные) такие, что
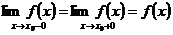 (29)
(29)
Точки разрыва I рода
1. Если существуют односторонние пределы в точке 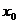 (конечные) и
(конечные) и
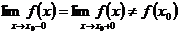 ,
,
то 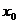 называется точкой устранимого разрыва.
называется точкой устранимого разрыва.
2. Если существует односторонние пределы в точке 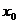 (конечные) и
(конечные) и 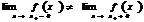 , (44)
, (44)
то 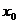 - точка разрыва, который называется скачок.
- точка разрыва, который называется скачок.
В случае устранимого разрыва функцию можно доопределить в точке 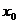 значением
значением 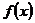 и она станет непрерывной.
и она станет непрерывной.
В случае скачка сделать это невозможно.
Точки разрыва II рода 
1. Если
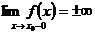 или
или 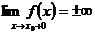
то 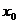 – точка разрыва, который называется бесконечный скачок. В этом случае прямая
– точка разрыва, который называется бесконечный скачок. В этом случае прямая 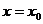 является вертикальной асимптотой.
является вертикальной асимптотой.
2. Если односторонние пределы в точке 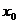 не существуют (не определены), то
не существуют (не определены), то 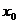 - точка неопределенности.
- точка неопределенности.
Получили, что 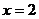 – точка разрыва I рода (скачка). Значит, функция непрерывна всюду на числовой прямой кроме точки
– точка разрыва I рода (скачка). Значит, функция непрерывна всюду на числовой прямой кроме точки 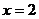 , в которой она имеет скачок, равный 1.
, в которой она имеет скачок, равный 1.
Первый способ вычисления
Используют метод логарифмического дифференцирования. Для этого:
1) логарифмируют обе части уравнения, которым задается функция (например, по основанию 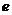 ):
):
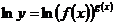 ,
,
получают
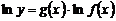 ;
;
2) дифференцируют обе части полученного равенства, где считают 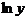 сложной функцией от
сложной функцией от 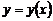 (правую часть равенства дифференцируют как произведение функций):
(правую часть равенства дифференцируют как произведение функций):
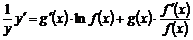
3) выражают из полученного равенства 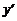 :
:
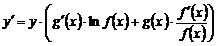 ;
;
4) заменяют y его выражением через x:
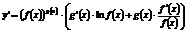 . (2)
. (2)
При решении данным методом используют не конечную формулу (2), а реализуют процесс логарифмического дифференцирования для каждой функции типа (1).
Второй способ
На основании свойства логарифмов записывают
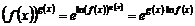 . (3)
. (3)
Далее дифференцируют как сложную функцию.
С помощью логарифмического дифференцирования удобно также вычислять производные функций при наличии в их аналитическом задании большого количества операций умножения, деления, возведения в степень.
Свойства дифференциала
Пусть 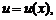
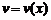 – дифференцируемые функции на некотором множестве
– дифференцируемые функции на некотором множестве 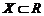 .
.
1) 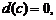
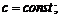
2) 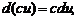
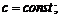
3) 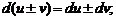
4) 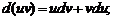
5) 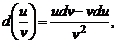
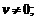
6) 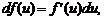 где
где 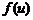 – сложная функция, дифференцируемая по переменной u (свойство инвариантности дифференциала). При достаточно малом значении
– сложная функция, дифференцируемая по переменной u (свойство инвариантности дифференциала). При достаточно малом значении 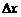 приращение функции с большой степенью точности можно заменить дифференциалом функции:
приращение функции с большой степенью точности можно заменить дифференциалом функции:
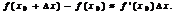
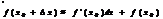 (11)
(11)
Формулу (11) используют в приближенных вычислениях.
С геометрической точки зрения дифференциал функции 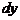 равен приращению ординаты касательной к кривой
равен приращению ординаты касательной к кривой 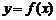 в точке
в точке 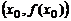 , когда аргумент получает приращение
, когда аргумент получает приращение 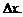
План исследования функции и построения графика
1. Найти область определения 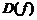 функции
функции 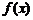 .
.
2. Найти область значений 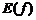 (если это возможно вначале, часто
(если это возможно вначале, часто 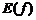 можно указать только по результатам исследования).
можно указать только по результатам исследования).
3. Исследовать функцию на четность.
4. исследовать на периодичность.
5. Найти точки пересечения с осями Ox (нули функции) и Oy.
6. Найти промежутки знакопостоянства функции.
7. Исследовать на непрерывность, дать классификацию разрывов.
8. Найти асимптоты графика функции (горизонтальную, вертикальную, наклонную).
9. Исследовать на монотонность и экстремум.
10. Исследовать на выпуклость, вогнутость, перегиб.
11. Построить график функции.
В.2 Матрицы и операции над ними
Матрицейназывается прямоугольная таблица, составленная из элементов некоторого множества. Горизонтальные ряды такой таблицы называются строками матрицы, а вертикальные – ее столбцами. Матрицы обозначают A, B, C, X … . Запись aij используется для указания местоположения элемента матрицы (i – номер строки, j – номер столбца). Числовую матрицу размера 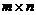 (то есть состоящую из m строк и n столбцов чисел) в общем случае записывают в виде:
(то есть состоящую из m строк и n столбцов чисел) в общем случае записывают в виде:
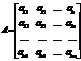
или в более компактной форме 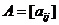 ,
, 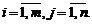 .
.
Eё обозначают также 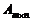 .
.
Если 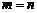 , то матрицу называют квадратной и обычно обозначают An. Элементы aii, (
, то матрицу называют квадратной и обычно обозначают An. Элементы aii, ( 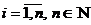 ) такой матрицы образуют ее главную диагональ.
) такой матрицы образуют ее главную диагональ.
Квадратная матрица вида 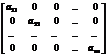 , (1)
, (1)
где 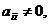
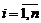 , называется диагональной. Если
, называется диагональной. Если 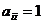 для любого
для любого 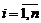 , то матрица (1) называется единичной и обозначается En.
, то матрица (1) называется единичной и обозначается En.
Верхней и нижней треугольной матрицами называются квадратные матрицы вида
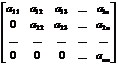 и
и 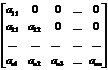
соответственно.
Трапециевидной матрицей называется матрица вида
 ,
,
где числа a11, a12, …, akk отличны от нуля.
Нулевой матрицей называется матрица, все элементы которой равны нулю. Обозначают такую матрицу буквой O.
Две матрицы одинакового размера
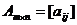 и
и 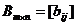 (2)
(2)
называются равными, если 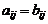 для всех
для всех 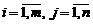 .
.
Суммой матриц (2) называется матрица A+B размера m×n, состоящая из элементов 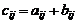 , где
, где 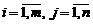 .
.
Произведением матрицы Am×n на число α называется матрица 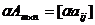 .
.
Разностью матриц (2) называется матрица A–B = A+ (–1)B.
Свойства операций сложения матриц и умножения на число:
1) 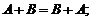
2) 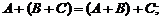
3) 0·A=О;
4) 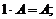
5) 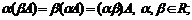
6) 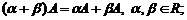
7) 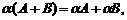
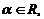 A и B – матрицы одинакового размера.
A и B – матрицы одинакового размера.
Для матриц A и B может быть введена операция умножения A·B при условии, что матрицы согласованы, т. е. количество столбцов матрицы A равно количеству строк матрицы B.
Произведением матрицы Al×m на матрицу Bm×n называется матрица 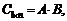 элементы которой
элементы которой
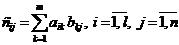 .
.
Для получения элемента 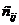 матрицы – произведения умножают последовательно каждый элемент
матрицы – произведения умножают последовательно каждый элемент 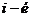 строки матрицы А на каждый элемент j-го столбца матрицы В и находят сумму этих произведений.
строки матрицы А на каждый элемент j-го столбца матрицы В и находят сумму этих произведений.
