Уравнение прямой в пространстве. Взаимное

Расположение прямых

Положение прямой в пространстве относительно прямоугольной системы координат однозначно определено, если известны координаты ее направляющего вектора 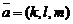и некоторой фиксированной точки 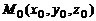этой прямой. Тогда радиус-вектор 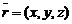произвольной точки M, лежащей на прямой, может быть представлен в виде

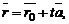
где 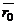– радиус-вектор точки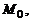 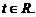Полученное веккторно-параметрическое уравнение в координатной форме равносильно трем параметрическим уравнениям:

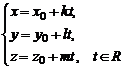
Исключая параметр t, придем к параметрическим уравнениям:

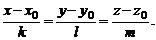
Прямую в пространстве можно задать и как линию пересечения двух плоскостей, заданных общими уравнениями, т. е. системой линейных уравнений:

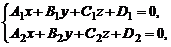
где коэффициенты при неизвестных не являются пропорциональными.

Расстояние 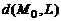от точки 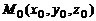до прямой L с направляющим вектором 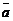и проходящей через точку 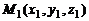может быть найдено по формуле

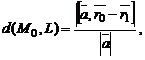
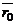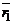где и – радиус-векторы точек 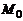и 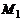соответственно.

Эту формулу можно использовать и для нахождения расстояния между параллельными прямыми.

Если прямые 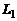и 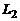являются скрещивающимися, то расстояние между ними

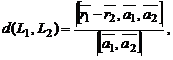
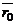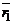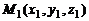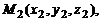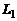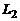где и – радиус-векторы точек и принадлежащих прямым и соответственно, а векторы 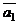и – и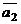х направляющие векторы.

О взаимном расположении двух прямых в пространстве можно судить по их направляющим векторам.

Прямые параллельны при условии коллинеарности их направляющих векторов (координаты пропорциональны).

Прямые перпендикулярны при условии перпендикулярности их направляющих векторов (скалярное произведение равно 0).

Угол между прямыми можно определить через косинус угла между направляющими векторами.

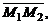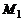Прямые лежат в одной плоскости при условии компланарности их направляющих векторов и вектора где и 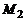– точки этих прямых (смешанное произведение равно 0).

Расстояние от точки 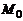до прямой L

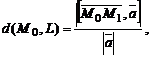
где 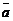– направляющий вектор, 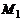– точка прямой.

Прямая и плоскость в пространстве

Пусть прямая L задана каноническими уравнениями:

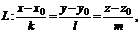
где 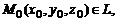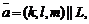а плоскость P – общим:

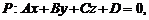
где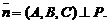

Тогда взаимное расположение прямой L и плоскости P в пространстве можно определить по направляющему вектору 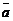прямой L и нормальному вектору 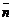плоскости P.

1.

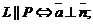
2.

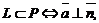
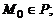
3.

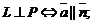
4. 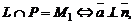координаты точки пересечения могут быть найдены следующим образом. От канонических уравнений прямой следует перейти к параметрическим, после чего подставить найденные значения 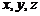в уравнение плоскости. Разрешить полученное уравнение относительно параметра t. Найденное значение 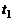подставить в параметрические уравнения, что позволит найти значения 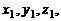которые и будут координатами искомой точки 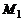пересечения прямой L и плоскости P.

Углом 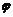между и плоскостью называется угол между прямой и ее ортогональной проекцией на плоскость, т. е.

.

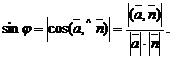
Кривые линии 2-го порядка.

Кривые 2го порядка описываются с помощью общего ур-я:

Ax²+2Bxy+Cy²+2Dx+2Ey+F=0, где

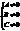
а) Каноническое ур-е эллипса

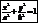- Каноническое ур-е эллипса

Если a=b, то x²+b²=a² - ур-е окружности.

б) Ур-е гиперболы: x²/a²-y²/b²=1

в) ур-е параболы: y²=2px или y=ax²

г) ур-е сферы: x²+y²+z²=а² (r²=(x-a)²+(y-b)²+(z-c)²)

д) ур-е эллипса: x²/a²-y²/b²+z²/c²=1

Парабола и ее свойства.

Множество точек плоскости, координаты которых по отношению к системе декартовых координат удовлетворяет уравнению y=ax², где х и у - текущие координаты, а- нек. число, наз. параболой.

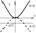Если вершина нах. в О(0,0), то ур-е примет вид

y²=2px-симметрично отн. оси ОХ

х²=2pу-симметрично отн. оси ОУ

Точка F(p/2,0) наз. фокусом параболы, а прямая x=-p/2 - ее директриса.

Любой точке М(х,у), принадлежащей параболе, расстояние до фокуса = r=p/2

Св-ва:

1. парабола предст. собой ¥ точек плоскости, равноотстающих от фокуса и от директрисы y=ax².

25.Эллипс и его св-ва:

Кривая второго порядка наз. эллипсом если коэффициенты А и L имеют одинаковые знаки

Аx²+Cy²=d

ур.-е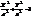

наз. канонич. ур.-ем эллипса, где 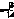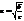При а=в представляет собой ур-е окружности х²+y²=а²

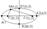
Точки F₁(-c,0) и F₂(c,0) - наз. фокусами эллипса а.

Отношение e=с/а наз. его эксцентриситетом (0<=e<=1)

Точки A₁,A₂,B₁,B₂ -вершины эллипса.

Св-во:
Для любой точки эллипса сумма расстояний этой точки до фокусов есть величина постоянной, =2а.

Гипербола и ее св-ва.

Кривая 2го порядка наз. гиперболой, если в ур-ии Ax²+Cy²=d, коэффициент А и С имеют противоположные знаки, т.е. А*С<0

б) Если d>0, то каноническое ур-е гиперболы примет вид: x²/a²-y²/b²=1, F1(c,o) и F₂(-c,0) - фокусы ее, e>0, e=c/a - эксцентриситет.

Св-во:
для любой точки гиперболы абсолютная величина разности ее расстояний до фокусов есть величина постоянная = 2а.

б) если d=0, ур-е примет вид x²/a²-y²/b²=0, получаем 2 перекрестные прямые х/а±у/b=0

в) если d<0, то x²/a²-y²/b²=-1 - ур-е сопряженной гиперболы.

.