В.4 Матрицы и операции над ними

В.5 ,6 Определители, их свойства и вычисление

Каждой квадратной матрице A порядка n можно поставить в соответствие единственное число, которое вычисляется по определенному правилу. Это число называется определителем (или детерминантом) матрицы A и обозначается |A|, или det A, или Δ(A). Порядок матрицы A является и порядком ее определителя. Определители порядка 1-3 определяются, соответственно, равенствами:

,

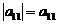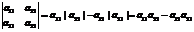, (3)

.

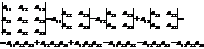Минором M_ij элемента a_ij , 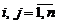, называется определитель (n-1)-го порядка, который состоит из элементов матрицы, полученной из данной после «вычеркивания» i- той строки и j-того столбца.

Алгебраическим дополнением элемента a_ijназываетсячисло А_ij=(-1)^i+jM_ij.Определитель порядка n, где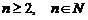

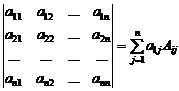, определяется как число.

Последнее равенство называют разложением определителя по элементам первой строки. Оно есть обобщение равенств (3).

Свойства определителей:

1) ;

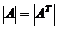2) ;

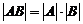3) общий множитель элементов какой-либо строки (столбца) можно вынести за знак определителя;

4) перестановка двух строк (столбцов) меняет знак определителя на противоположный;

5) |A|=0, если выполняется одно из следующих условий:

· в определителе есть нулевая строка (нулевой столбец),

· в определителе есть пропорциональные строки (столбцы),

· в определителе есть строки (столбцы), являющиеся линейной комбинацией соответствующих элементов других строк (столбцов);

6) если к элементам одной строки (столбца) определителя прибавить линейную комбинацию соответствующих элементов других строк (столбцов), то значение определителя не изменится.

Основные методы вычисления определителей.

1. Для определителей 3-го порядка удобно использовать правило треугольников, которое схематично можно изобразить следующим образом:

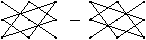
Линии соединяют по три элемента, которые умножаются, а затем произведения складываются.

2. Определитель порядка n может быть вычислен разложением по любой строке (столбцу):

.

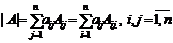3. Метод эффективного понижения порядка определителя: используя свойства определителя, его преобразуют к такому виду, чтобы все элементы некоторой строки (столбца) определителя, кроме одного, были нулями, затем вычисляют определитель разложением по этой строке (столбцу).

4. Метод приведения к треугольному или диагональному виду с использованием свойств определителя, когда определитель равен произведению диагональных элементов.

.

Метод окаймляющих миноров

Если в матрице A найден ненулевой минор M_k порядка k, 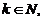а все окаймляющие его миноры 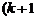)-го порядка равны нулю, то ранг матрицы равен k ( ).

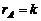Метод элементарных преобразований

Используя элементарные преобразования строк, матрицу приводят к трапециевидной или треугольной форме, далее ранг находят по определению.

Как частный случай последнего метода, может быть рассмотрен метод нулей и единиц: элементарными преобразованиями строк матрицу приводят к эквивалентной, состоящей или из нулевых строк и столбцов, или из строк и столбцов, в которых содержится ровно одна единица, а остальные элементы – нулевые. Количество единиц в такой матрице равно ее рангу.

В.13 Векторное произведение

Векторным произведением 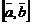двух векторов 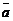и 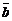называется вектор, удовлетворяющий следующим условиям:

1) ;

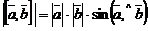2)

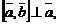
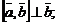
3) тройка векторов 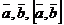– правая.

Векторное произведение обозначают также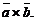

Если хотя бы один из векторов 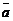или 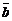нулевой, то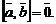

Геометрический смысл векторного произведения 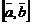состоит в том, что длина этого вектора численно равна площади параллелограмма, построенного на векторах 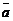и :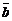

..

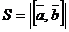Свойства векторного произведения:

1) ;

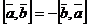2) ;

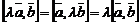3) ;

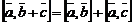4) 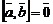при 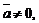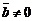тогда и только тогда, когда векторы 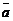и 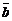коллинеарны.

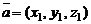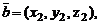Если и то

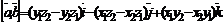
Последнюю формулу удобно записать в виде формального определения третьего порядка:

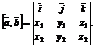
Плоскость в пространстве

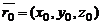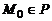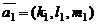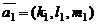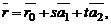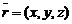1. Положение плоскости P в пространстве относительно прямоугольной системы координат Oxyz однозначно определено, если задан радиус-вектор некоторой фиксированной точки и два некомпланарных вектора и , параллельных данной плоскости. В этом случае равенство где – радиус-вектор произвольной точки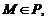 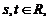называется векторно-параметрическим уравнением плоскости P. Записав его в координатной форме получим параметрические уравнения плоскости.

2. Эту же плоскость можно задать одним из уравнений:

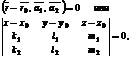(1)

справедливость которых обусловлена условием компланарности векторов 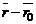, 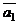и .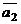

3. Координаты векторов 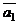и 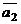могут быть найдены, если известны три точки плоскости P, не лежащие на одной прямой: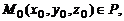

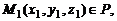
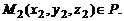
В этом случае 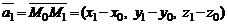, 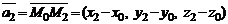. В результате имеем уравнение плоскости, проходящей через три заданные точки, не лежащие на одной прямой.

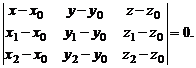
4. Если известны точки пересечения плоскости P с координатными осями, т. е. M₀(a, 0, 0), M₁(0, b, 0), M₂(0, 0, c), то справедливо уравнение «в отрезках»:

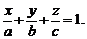
5. Положение плоскости P в пространстве однозначно определено и в том случае, когда задан нулевой нормальный вектор 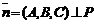и точка 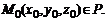Условия перпендикулярности векторов 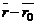и 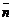позволят перейти к векторному уравнению 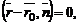а затем к его координатной форме записи:

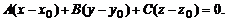(2)

После преобразования последнего уравнения приходим к общему уравнению плоскости P:

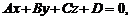где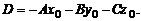

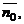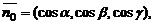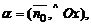
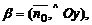
6. Если в качестве нормального вектора плоскости P взять единичный вектор направленный из начала координат в сторону плоскости, то где 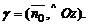Тогда справедливо нормальное уравнение плоскости

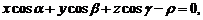
где 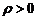– расстояние от начала координат до плоскости.

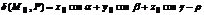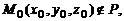Величина , где называется отклонением точки 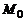от плоскости 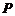. При этом 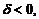если 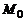и O(0, 0, 0) лежат по одну сторону от плоскости, 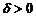– если лежат по разные, 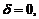если 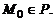Расстояние 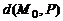от точки 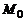до плоскости 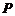равно абсолютному значению ее отклонения, т. е.

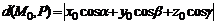.От общего уравнения плоскости к нормальному можно перейти с помощью умножения на нормирующий множитель

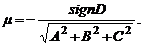
Значит, расстояние 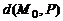от точки 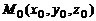до плоскости 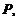заданной общим уравнением 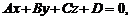может быть найдено по формуле

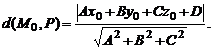
Угол 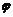между плоскостями в пространстве определяется по косинусу угла между нормальными векторам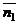и и 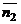этих плоскостей:

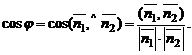
Расположение прямых

Положение прямой в пространстве относительно прямоугольной системы координат однозначно определено, если известны координаты ее направляющего вектора 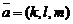и некоторой фиксированной точки 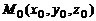этой прямой. Тогда радиус-вектор 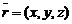произвольной точки M, лежащей на прямой, может быть представлен в виде

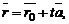
где 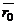– радиус-вектор точки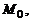 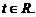Полученное веккторно-параметрическое уравнение в координатной форме равносильно трем параметрическим уравнениям:

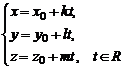
Исключая параметр t, придем к параметрическим уравнениям:

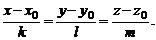
Прямую в пространстве можно задать и как линию пересечения двух плоскостей, заданных общими уравнениями, т. е. системой линейных уравнений:

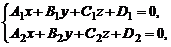
где коэффициенты при неизвестных не являются пропорциональными.

Расстояние 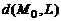от точки 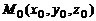до прямой L с направляющим вектором 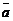и проходящей через точку 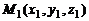может быть найдено по формуле

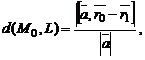
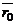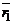где и – радиус-векторы точек 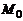и 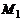соответственно.

Эту формулу можно использовать и для нахождения расстояния между параллельными прямыми.

Если прямые 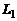и 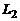являются скрещивающимися, то расстояние между ними

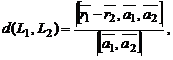
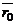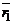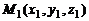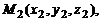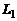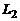где и – радиус-векторы точек и принадлежащих прямым и соответственно, а векторы 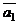и 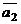– их направляющие векторы.

О взаимном расположении двух прямых в пространстве можно судить по их направляющим векторам.

Прямые параллельны при условии коллинеарности их направляющих векторов (координаты пропорциональны).

Прямые перпендикулярны при условии перпендикулярности их направляющих векторов (скалярное произведение равно 0).

Угол между прямыми можно определить через косинус угла между направляющими векторами.

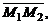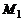Прямые лежат в одной плоскости при условии компланарности их направляющих векторов и вектора где и 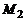– точки этих прямых (смешанное произведение равно 0).

Расстояние от точки 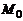до прямой L

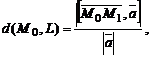
где 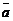– направляющий вектор, 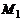– точка прямой.

Кривые линии 2-го порядка.

Кривые 2го порядка описываются с помощью общего ур-я:

Ax²+2Bxy+Cy²+2Dx+2Ey+F=0, где

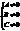
а) Каноническое ур-е эллипса

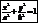- Каноническое ур-е эллипса

Если a=b, то x²+b²=a² - ур-е окружности.

б) Ур-е гиперболы: x²/a²-y²/b²=1

в) ур-е параболы: y²=2px или y=ax²

г) ур-е сферы: x²+y²+z²=а² (r²=(x-a)²+(y-b)²+(z-c)²)

д) ур-е эллипса: x²/a²-y²/b²+z²/c²=1

Парабола и ее свойства.

Множество точек плоскости, координаты которых по отношению к системе декартовых координат удовлетворяет уравнению y=ax², где х и у - текущие координаты, а- нек. число, наз. параболой.

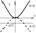Если вершина нах. в О(0,0), то ур-е примет вид

y²=2px-симметрично отн. оси ОХ

х²=2pу-симметрично отн. оси ОУ

Точка F(p/2,0) наз. фокусом параболы, а прямая x=-p/2 - ее директриса.

Любой точке М(х,у), принадлежащей параболе, расстояние до фокуса = r=p/2

Св-ва:

1. парабола предст. собой ¥ точек плоскости, равноотстающих от фокуса и от директрисы y=ax².

25.Эллипс и его св-ва:

Кривая второго порядка наз. эллипсом если коэффициенты А и L имеют одинаковые знаки

Аx²+Cy²=d

ур.-е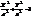

наз. канонич. ур.-ем эллипса, где 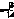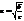При а=в представляет собой ур-е окружности х²+y²=а²

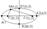
Точки F₁(-c,0) и F₂(c,0) - наз. фокусами эллипса а.

Отношение e=с/а наз. его эксцентриситетом (0<=e<=1)

Точки A₁,A₂,B₁,B₂ -вершины эллипса.

Св-во:
Для любой точки эллипса сумма расстояний этой точки до фокусов есть величина постоянной, =2а.

Гипербола и ее св-ва.

Кривая 2го порядка наз. гиперболой, если в ур-ии Ax²+Cy²=d, коэффициент А и С имеют противоположные знаки, т.е. А*С<0

б) Если d>0, то каноническое ур-е гиперболы примет вид: x²/a²-y²/b²=1, F1(c,o) и F₂(-c,0) - фокусы ее, e>0, e=c/a - эксцентриситет.

Св-во:
для любой точки гиперболы абсолютная величина разности ее расстояний до фокусов есть величина постоянная = 2а.

б) если d=0, ур-е примет вид x²/a²-y²/b²=0, получаем 2 перекрестные прямые х/а±у/b=0

в) если d<0, то x²/a²-y²/b²=-1 - ур-е сопряженной гиперболы.

.

В.4 Матрицы и операции над ними

Матрицейназывается прямоугольная таблица, составленная из элементов некоторого множества. Горизонтальные ряды такой таблицы называются строками матрицы, а вертикальные – ее столбцами. Матрицы обозначают A, B, C, X … . Запись a_ij используется для указания местоположения элемента матрицы (i – номер строки, j – номер столбца). Числовую матрицу размера 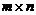(то есть состоящую из m строк и n столбцов чисел) в общем случае записывают в виде:

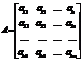
или в более компактной форме , .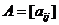

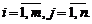Eё обозначают также .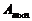

Если 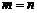, то матрицу называют квадратной и обычно обозначают A_n. Элементы a_ii, ( 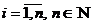) такой матрицы образуют ее главную диагональ.

Квадратная матрица вида 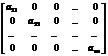, (1)

где 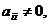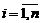, называется диагональной. Если 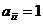для любого 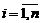, то матрица (1) называется единичной и обозначается E_n.

Верхней и нижней треугольной матрицами называются квадратные матрицы вида

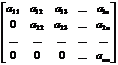и

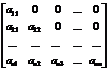
соответственно.

Трапециевидной матрицей называется матрица вида

,

где числа a₁₁, a₁₂, …, a_kk отличны от нуля.

Нулевой матрицей называется матрица, все элементы которой равны нулю. Обозначают такую матрицу буквой O.

Две матрицы одинакового размера

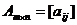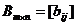и (2)

называются равными, если 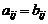для всех .

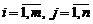Суммой матриц (2) называется матрица A+B размера m×n, состоящая из элементов 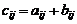, где .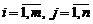

Произведением матрицы A_m×n на число α называется матрица .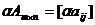

Разностью матриц (2) называется матрица A–B = A+ (–1)B.

Свойства операций сложения матриц и умножения на число:

1)

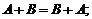
2)

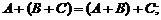
3) 0·A=О;

4)

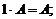
5)

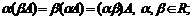
6)

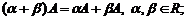
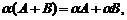
7) 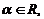A и B – матрицы одинакового размера.

Для матриц A и B может быть введена операция умножения A·B при условии, что матрицы согласованы, т. е. количество столбцов матрицы A равно количеству строк матрицы B.

Произведением матрицы A_l×m на матрицу B_m×n называется матрица 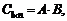элементы которой

.

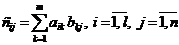Для получения элемента 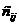матрицы – произведения умножают последовательно каждый элемент 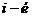строки матрицы А на каждый элемент j-го столбца матрицы В и находят сумму этих произведений.

Свойства операции умножения матриц:

1)

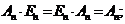
2)

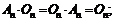
3)

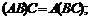
4)

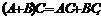
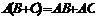
В общем случае из существования AB не следует существование BA. Даже если оба эти произведения определены, они не всегда равны. Матрицы, для которых 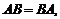называются коммутативными.

Пусть A – квадратная матрица. Тогда k-я степень ( 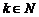) матрицы A определяется равенством 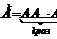. По определению принимают 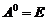при условии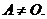

Матрица A^T , полученная из матрицы A заменой столбцов строками с теми же номерами, называется транспонированной к матрице A, то есть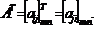

Свойства операции транспонирования матриц:

1)

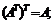
2)

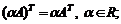
3)

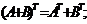
4)

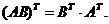
Если для квадратной матрицы A выполняется соотношение 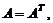то матрица A называется симметрической матрицей, а если 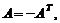– то кососимметрической.

Элементарными преобразованиями над строками матрицы A называют следующие операции:

1) перестановку строк;

2) умножение строки на ненулевое число;

3) прибавление к элементам строки соответствующих элементов другой строки, умноженных на ненулевое число.

Говорят, что матрица A эквивалентна матрице B (пишут: A~B), если матрица B получена из A при помощи элементарных преобразований строк.