Зависимые и независимые, совместные и несовместные события.
Событие А называется зависимым от события В, если вероятность события А зависит от того, произошло событие В или нет.
Событие A называют независимым от события B, если появление события B не изменяет вероятности появления события A.
Если появление одного события исключает появление другого, то они называются несовместными; в противном случае два события называются совместными.
Формула сложения вероятностей для любых двух событий.
Теорема 1: Если события несовместны, то вероятность суммы событий равна сумме вероятностей этих событий.
Р(А + В) = Р(А) + Р(В). (2.7)
Доказательство:
N – число всех исходов испытаний.
m1 – число исходов испытаний, благоприятствующих наступлению события А.
m2 – число испытаний, благоприятствующих наступлению события В.
Р(А + В) = 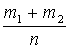 =
= 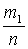 +
+ 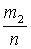 = Р(А) + Р(В). Что и требовалось доказать.
= Р(А) + Р(В). Что и требовалось доказать.
Следствие из теоремы:
Вероятность суммы нескольких несовместных событий равна сумме вероятности этих событий.
Р(А1 + А2 + … + Аn) = Р(А1) + Р(А2) + … + Р(Аn)
Теорема 2: Сумма вероятностей событий, образующих полную группу, равна единице.
Доказательство:
Пусть А1,А2, …, Аn – полная группа событий. Тогда наступление одного из этих событий – событие достоверное, т.е. Р(А1 + А2 + … +Аn) = 1. Но по теореме сложения несовместных событий можно записать:
Р(А1) + Р(А2) + … Р(А) = 1.
Следствие из теоремы:
Сумма вероятностей противоположных событий равна 1. Р(А) + Р(Ā) = 1.
Теорема 3: Если события совместны, то вероятность их суммы вычисляется по формуле:
Р(А + В) = Р(А) + Р(В) – Р(А×В)
Доказательство:
m1 – число исходов испытаний, благоприятствующих наступлению события А.
m2 – число исходов испытаний, благоприятствующих наступлению события В.
m3 – число исходов испытаний, благоприятствующих наступлению совместных событий А×В.
N – число всех исходов испытаний.
Р(А + В) = 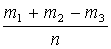 =
= 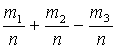 = Р(А) + Р(В) – Р(А×В).Что и требовалось доказать.
= Р(А) + Р(В) – Р(А×В).Что и требовалось доказать.
Формулы умножения вероятностей для любых событий.
Теорема умножения: Вероятность произведения событий равна вероятности одного из этих событий, умноженной на условную вероятность другого при условии, что первое событие уже произошло.
Р(А × В) = Р(А) × РA(В).
Доказательство:
N – число всех исходов испытания.
M – число исходов, благоприятствующих наступлению события А.
К – число исходов, благоприятствующих наступлению события В, при условии, что А имело место, т.е. к – число исходов, когда А и В наступили вместе.
Поэтому Р(А × В) = 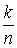 =
= 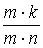 =
=  = P(A) × PA(B).
= P(A) × PA(B).
Теорема умножения вероятностей обобщается на случай произвольного числа событий:
Р(АВСD) = Р(А)· РA(В) ·РAB(С) · РABC(D), т.е. вероятность произведения нескольких событий равна произведению вероятности одного из этих событий на условные вероятности других; при этом условная вероятность каждого последующего события вычисляется в предположении, что все предыдущие события произошли.
Следствия.
Если события независимы, то вероятность события В, при условии, что А наступило.
РA(В) = Р(В).
РA(А) = P(A).
