Дифференциал: определение, геометрический и физический смысл.

Дифференциалом функции называется главная, линейная относительно часть приращения функции, равная произведению производной на приращение независимой переменной: .

Дифференциал функции имеет простой геометрический смысл: значение дифференциала функции, при данном значении аргумента и данном при­ращении , равно прираще­нию ординаты касательной,, проведенной в точке с абсцис­сой графика этой функции, при переходе от точки каса­ния (с абсциссой ) к соседней точке касательной с абсциссой .

В самом деле, соответст­вующее приращение ординаты касательной на рис. 4.5 изо­бражается катетом KN треу­гольника MKN, в котором вторым катетом служит от­резок МК= , а острый угол при вершине М равен , причем Но тогда KN = МК что и требовалось доказать.

Отметим одно характерное свойство дифференциала функции: дифферен­циал сложной функции, т. е. функции, зависящей от аргумента через промежуточный аргумент 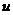, все же равен, как и в случае простой функции (см. 4.64*), произведению производной от этой функции по промежуточ­ному аргументу на дифференциал этого аргумента. Таким образом, если , где , то (4.67) В самом деле, по правилу дифференцирования сложной функции имеем Отсюда, умножая на , находим Но и, следовательно, , что и требовалось доказать. Это свойство дифференциала называют свойством инвариантности, т. е. свойством неизменности формы записи дифференциала функции, как в случае простой, так и в случае сложной функции. [Производная, как нам известно, свойством инвариантности не обладает: § 3, (4.21).]

I. Правила дифференцирования	II. Формулы дифференцирования
1. 2. 3. 4. 5.	1. 2. 3. 4. 5. 6. 7.

30. Производные и дифференциалы второго порядка: определения и методы их вычисления.

Производную от производной данной функции, если она существует, называют производной второго порядка, или второй производной, от данной функции и обозначают символом . Таким образом

(4.56). В связи с этим производную в дальнейшем будем называть производной первого порядка, или первой производной.

Рассмотрим несколько примеров отыскания производных высших порядков.

1. Найти производную порядка от функции .

Находим, выполняя последовательные дифференцирования: .

2. Найти производную порядка от функций и .

Первую производную от , равную , можно записать в следующем виде:

отсюда следует, что операция дифференцирования функции по формально сводится к прибавлению к аргументу синуса. В силу этого ; поэтому . Аналогично, ; поэтому и вообще

. Аналогично можно убедиться в том, что если , то .

3. Найти производную порядка от функции . Имеем ,

откуда, заметив общий закон образования последовательных производных, находим .

4. Найти производную порядка от функции ( - любое действительное число).

Имеем последовательно откуда, заметив общий закон образования производных, находим

В частном случае, когда ( 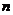- целое положительное число), . Все же дальнейшие производные от будут равны нулю, как производные от постоянного.

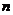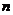Отсюда следует, что если целая рациональная функция степени от (многочлен степени относительно ):

,

, а .

Дифференциалом второго порядка (его обозначают символом ) от функции называют дифференциал ее дифференциала: (4.69)

Найдем его выражение. Имеем , причем — произвольное приращение аргумента , которое от аргумента не зависит. В виду этого при отыскании второго дифференциала функции надо рассматривать диф­ференциал независимого переменного как величину постоянную относи­тельно аргумента .

Находим

Таким образом, второй дифференциал функции равен произведению ее второй производной на квадрат дифференциала независимого переменного:

Если дифференциал 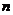-го порядка (обозначение ) уже введен, то дифференциалом -го порядка будет дифференциал дифференциала 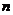-го порядка:

Докажем методом индукции справедливость следующей формулы:

(4. 72)

Исходя из формулы (4.72), найдем , как дифференциал от :

Поскольку для получено такое же выражение, как и для , можно утверждать, что формула (4.72) справедлива при всяком 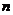, так как при она доказана [см. (4.70)]. Из формулы (4.72) получим выражение для производной 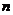-го поряд­ка через отношение дифференциалов: (4.73)

Таким обозначением производных 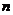-го порядка в анализе часто поль­зуются наряду с обозначениями и .

Дифференциалы высших порядков, начиная со второго, вообще говоря, не обладают свойством инвариантности: структура дифференциала сложной функции иная, чем дифференциала функции простой.

Убедимся в этом на примере дифференциала второго порядка. Пусть , . В силу инвариантности первого дифференциала , имеем:

Но так как 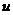— функция от , то уже не будет величиной постоянной относительно . Поэтому дифференциал от надо искать как дифференциал произведения:

Таким образом, уже в выражении второго дифференциала сложной функции появляется дополнительное слагаемое , зависящее от второго дифференциала промежуточного аргумента. Это же будет иметь место и для дифференциалов более высоких порядков. Тем самым в общем случае утверждение наше доказано.

Примечание. Свойство инвариантности у дифференциалов второго и высших порядков сохраняется лишь тогда, когда промежуточный аргумент 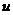является линей­ной функцией независимого переменного :