Основные свойства векторного произведения
1. Векторное произведение двух векторов 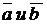 равно нулевому вектору в том и только в том случае, когда эти векторы параллельны. Из этого свойства следует, что векторное произведение любого вектора на самого себя, т.е.
равно нулевому вектору в том и только в том случае, когда эти векторы параллельны. Из этого свойства следует, что векторное произведение любого вектора на самого себя, т.е. 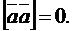
2. Векторное произведение двух векторов антикоммутативно, а именно:
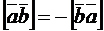
3. Векторное произведение обладает свойствами сочетательности относительно числового множителя:
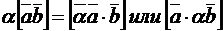 , т.е. чтобы умножить векторное произведение векторов на число достаточно умножить на это число один из сомножителей.
, т.е. чтобы умножить векторное произведение векторов на число достаточно умножить на это число один из сомножителей.
4. Векторное произведение векторов обладает распределительным свойством относительно векторов, т. е.
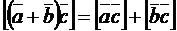 .
.
5. Если векторы 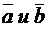 перпендикулярны, то
перпендикулярны, то 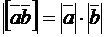
Векторное произведение векторов 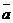 =
= 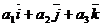 и
и 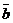 =
= 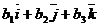 в координатной форме вычисляется по формуле:
в координатной форме вычисляется по формуле:
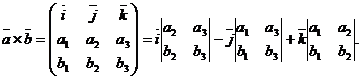
Смешанным произведением трех векторов 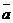 ,
, 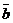 и
и 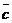 называется скалярное произведение вектора
называется скалярное произведение вектора 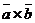 на вектор
на вектор 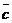 . Обозначается (
. Обозначается ( 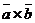 )
) 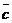 .
.
Геометрический смысл смешанного произведения трех векторов дается в следующей теореме.
Теорема 1. Смешанное произведение некомпланарных векторов 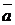 ,
, 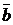 и
и 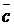 по модулю равно объему параллелепипеда, построенного на этих векторах.
по модулю равно объему параллелепипеда, построенного на этих векторах.
Теорема 2. Смешанное произведение векторов 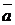 ,
, 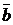 ,
, 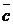 положительно, если тройка векторов
положительно, если тройка векторов 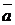 ,
, 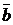 ,
, 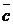 правая и отрицательно, если она левая.
правая и отрицательно, если она левая.
Действительно, по определению 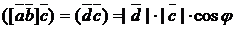 .
.
Поэтому знак смешанного произведения зависит от знака cosj. Если теперь тройка векторов правая, то векторы 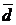 и
и 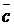 образуют острый угол и cosj > 0. Если же тройка векторов левая, то векторы
образуют острый угол и cosj > 0. Если же тройка векторов левая, то векторы 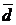 и
и 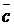 образуют тупой угол cosj < 0.
образуют тупой угол cosj < 0.
Теорема 3. Смешанное произведение векторов 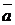 ,
, 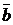 ,
, 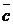 равно нулю тогда и только тогда, когда эти векторы компланарны.
равно нулю тогда и только тогда, когда эти векторы компланарны.
Смешанное произведение векторов 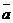 =
= 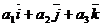 ,
, 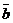 =
= 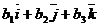 и
и 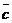 =
= 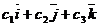 в координатной форме есть определитель:
в координатной форме есть определитель: 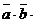
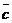 =
= 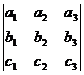 .
.
Уравнение прямой на плоскости: с угловым коэффициентом, через две точки, в отрезках, общее уравнение.
Уравнение прямой с угловым коэффициентом
Рассмотрим в двумерном пространстве (т.е. на плоскости) прямую линию не параллельную оси OY.
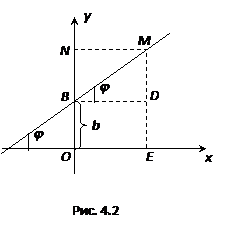
Обозначим угол наклона прямой к оси OX через 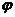 и
и 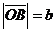 . Пусть точка М(x,y) произвольная точка прямой. MD=y-b; BD=x.
. Пусть точка М(x,y) произвольная точка прямой. MD=y-b; BD=x.
Из прямоугольного треугольника BDM имеем 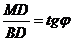 или
или 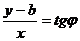 или
или 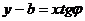 (4.8)
(4.8)
Определение. Тангенс угла наклона прямой к оси OX называется угловым коэффициентом прямой
и обозначают 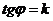 . Формулу (4.8), на основании данного определения, можно записать в виде:
. Формулу (4.8), на основании данного определения, можно записать в виде:
y-b=kx или y=kx+b (4.9)
В случае b=0, прямая y=kx проходит через начало координат.
Уравнение прямой, проходящей через две точки
Пусть даны две точки М1 и М2 и требуется написать уравнение прямой проходящей через две данные точки. Тогда, очевидно в качестве точки, лежащей на прямой можно взять любую из двух данных точек. Возьмем, например, точку М1. За направляющий вектор примем вектор 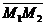 . Тогда, если рассмотреть точки на плоскости, то М1(x1,y1) и М2(x2,y2) и
. Тогда, если рассмотреть точки на плоскости, то М1(x1,y1) и М2(x2,y2) и 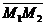 ={x2-x1,y2-y1} и уравнение имеет вид:
={x2-x1,y2-y1} и уравнение имеет вид: 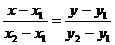 – каноническое уравнение прямой на плоскости.
– каноническое уравнение прямой на плоскости.
Уравнение прямой в отрезках
Пусть дана прямая линия, которая не проходит через начало координат и отсекает от координатных осей соответственно отрезки a и b, где a=вел.ОМ, b=вел.ОN.
Покажем, что уравнение этой прямой можно записать в виде 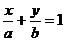 (4.11)
(4.11)
Действительно напишем уравнение прямой в общем виде 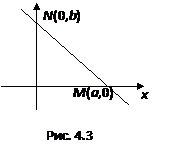
Ax+By+C=0 (4.12)
