График функции y=f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале. 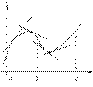 График функции y=f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале. На рисунке показана кривая, выпуклая на (a; b) и вогнутая на (b; c). Рассмотрим достаточный признак, позволяющий установить, будет ли график функции в данном интервале выпуклым или вогнутым. Теорема. Пусть y=f(x) дифференцируема на (a; b). Если во всех точках интервала (a; b) вторая производная функции y = f(x) отрицательная, т.е. f ''(x) < 0, то график функции на этом интервале выпуклый, если же f''(x) > 0 – вогнутый. Доказательство. Предположим для определенности, что f''(x) < 0 и докажем, что график функции будет выпуклым. График функции y=f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале. На рисунке показана кривая, выпуклая на (a; b) и вогнутая на (b; c). Рассмотрим достаточный признак, позволяющий установить, будет ли график функции в данном интервале выпуклым или вогнутым. Теорема. Пусть y=f(x) дифференцируема на (a; b). Если во всех точках интервала (a; b) вторая производная функции y = f(x) отрицательная, т.е. f ''(x) < 0, то график функции на этом интервале выпуклый, если же f''(x) > 0 – вогнутый. Доказательство. Предположим для определенности, что f''(x) < 0 и докажем, что график функции будет выпуклым.  Возьмем на графике функции y = f(x) произвольную точку M0 с абсциссой x0 Î (a; b) и проведем через точку M0 касательную. Ее уравнение Возьмем на графике функции y = f(x) произвольную точку M0 с абсциссой x0 Î (a; b) и проведем через точку M0 касательную. Ее уравнение 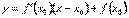 . Мы должны показать, что график функции на (a; b) лежит ниже этой касательной, т.е. при одном и том же значении x ордината кривой y = f(x) будет меньше ордината касательной. Итак, уравнение кривой имеет вид y = f(x). Обозначим . Мы должны показать, что график функции на (a; b) лежит ниже этой касательной, т.е. при одном и том же значении x ордината кривой y = f(x) будет меньше ордината касательной. Итак, уравнение кривой имеет вид y = f(x). Обозначим 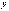 ординату касательной, соответствующую абсциссе x. Тогда ординату касательной, соответствующую абсциссе x. Тогда 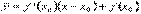 . Следовательно, разность ординат кривой и касательной при одном и том же значении x будет . Следовательно, разность ординат кривой и касательной при одном и том же значении x будет 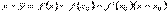 . Разность f(x) – f(x0) преобразуем по теореме Лагранжа . Разность f(x) – f(x0) преобразуем по теореме Лагранжа 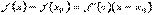 , где c между x и x0. Таким образом, , где c между x и x0. Таким образом, 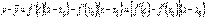 . К выражению, стоящему в квадратных скобках снова применим теорему Лагранжа: . К выражению, стоящему в квадратных скобках снова применим теорему Лагранжа: 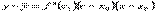 , где c1 между c0 и x0. По условию теоремы f ''(x) < 0. Определим знак произведения второго и третьего сомножителей. 1. Предположим, что x>x0. Тогда x0<c1<c<x, следовательно, , где c1 между c0 и x0. По условию теоремы f ''(x) < 0. Определим знак произведения второго и третьего сомножителей. 1. Предположим, что x>x0. Тогда x0<c1<c<x, следовательно,  (x – x0) > 0 и (c – x0) > 0. Поэтому (x – x0) > 0 и (c – x0) > 0. Поэтому 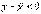 . 2. Пусть x<x0, следовательно, x < c < c1 < x0 и (x – x0) < 0, (c – x0) < 0. Поэтому вновь . 2. Пусть x<x0, следовательно, x < c < c1 < x0 и (x – x0) < 0, (c – x0) < 0. Поэтому вновь 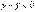 . Таким образом, любая точка кривой лежит ниже касательной к кривой при всех значениях x и x0 (a; b), а это значит, что кривая выпукла. Вторая часть теоремы доказывается аналогично. Точка графика непрерывной функции, отделяющая его выпуклую часть от вогнутой, называется точкой перегиба. Очевидно, что в точке перегиба касательная, если она существует, пересекает кривую, т.к. с одной стороны от этой точки кривая лежит под касательной, а с другой стороны – над нею. . Таким образом, любая точка кривой лежит ниже касательной к кривой при всех значениях x и x0 (a; b), а это значит, что кривая выпукла. Вторая часть теоремы доказывается аналогично. Точка графика непрерывной функции, отделяющая его выпуклую часть от вогнутой, называется точкой перегиба. Очевидно, что в точке перегиба касательная, если она существует, пересекает кривую, т.к. с одной стороны от этой точки кривая лежит под касательной, а с другой стороны – над нею.  Определим достаточные условия того, что данная точка кривой является точкой перегиба. Определим достаточные условия того, что данная точка кривой является точкой перегиба.  Теорема. Пусть кривая определяется уравнением y = f(x). Если f ''(x0) = 0 или f ''(x0) не существует и при переходе через значение x = x0 производная f ''(x) меняет знак, то точка графика функции с абсциссой x = x0 есть точка перегиба. Доказательство. Пусть f ''(x) < 0 при x < x0 и f ''(x) > 0 при x > x0. Тогда при x < x0 кривая выпукла, а при x > x0 – вогнута. Следовательно, точка A, лежащая на кривой, с абсциссой x0 есть точка перегиба. Аналогично можно рассматривать второй случай, когда f ''(x) > 0 при x < x0 и f ''(x) < 0 при x > x0. Таким образом, точки перегиба следует искать только среди таких точек, где вторая производная обращается в нуль или не существует. Теорема. Пусть кривая определяется уравнением y = f(x). Если f ''(x0) = 0 или f ''(x0) не существует и при переходе через значение x = x0 производная f ''(x) меняет знак, то точка графика функции с абсциссой x = x0 есть точка перегиба. Доказательство. Пусть f ''(x) < 0 при x < x0 и f ''(x) > 0 при x > x0. Тогда при x < x0 кривая выпукла, а при x > x0 – вогнута. Следовательно, точка A, лежащая на кривой, с абсциссой x0 есть точка перегиба. Аналогично можно рассматривать второй случай, когда f ''(x) > 0 при x < x0 и f ''(x) < 0 при x > x0. Таким образом, точки перегиба следует искать только среди таких точек, где вторая производная обращается в нуль или не существует. | |
 График функции y=f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале. На рисунке показана кривая, выпуклая на (a; b) и вогнутая на (b; c). Рассмотрим достаточный признак, позволяющий установить, будет ли график функции в данном интервале выпуклым или вогнутым. Теорема. Пусть y=f(x) дифференцируема на (a; b). Если во всех точках интервала (a; b) вторая производная функции y = f(x) отрицательная, т.е. f ''(x) < 0, то график функции на этом интервале выпуклый, если же f''(x) > 0 – вогнутый. Доказательство. Предположим для определенности, что f''(x) < 0 и докажем, что график функции будет выпуклым.
График функции y=f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале. На рисунке показана кривая, выпуклая на (a; b) и вогнутая на (b; c). Рассмотрим достаточный признак, позволяющий установить, будет ли график функции в данном интервале выпуклым или вогнутым. Теорема. Пусть y=f(x) дифференцируема на (a; b). Если во всех точках интервала (a; b) вторая производная функции y = f(x) отрицательная, т.е. f ''(x) < 0, то график функции на этом интервале выпуклый, если же f''(x) > 0 – вогнутый. Доказательство. Предположим для определенности, что f''(x) < 0 и докажем, что график функции будет выпуклым.  Возьмем на графике функции y = f(x) произвольную точку M0 с абсциссой x0 Î (a; b) и проведем через точку M0 касательную. Ее уравнение
Возьмем на графике функции y = f(x) произвольную точку M0 с абсциссой x0 Î (a; b) и проведем через точку M0 касательную. Ее уравнение 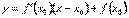 . Мы должны показать, что график функции на (a; b) лежит ниже этой касательной, т.е. при одном и том же значении x ордината кривой y = f(x) будет меньше ордината касательной. Итак, уравнение кривой имеет вид y = f(x). Обозначим
. Мы должны показать, что график функции на (a; b) лежит ниже этой касательной, т.е. при одном и том же значении x ордината кривой y = f(x) будет меньше ордината касательной. Итак, уравнение кривой имеет вид y = f(x). Обозначим 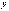 ординату касательной, соответствующую абсциссе x. Тогда
ординату касательной, соответствующую абсциссе x. Тогда 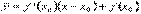 . Следовательно, разность ординат кривой и касательной при одном и том же значении x будет
. Следовательно, разность ординат кривой и касательной при одном и том же значении x будет 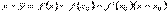 . Разность f(x) – f(x0) преобразуем по теореме Лагранжа
. Разность f(x) – f(x0) преобразуем по теореме Лагранжа 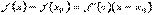 , где c между x и x0. Таким образом,
, где c между x и x0. Таким образом, 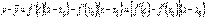 . К выражению, стоящему в квадратных скобках снова применим теорему Лагранжа:
. К выражению, стоящему в квадратных скобках снова применим теорему Лагранжа: 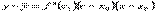 , где c1 между c0 и x0. По условию теоремы f ''(x) < 0. Определим знак произведения второго и третьего сомножителей. 1. Предположим, что x>x0. Тогда x0<c1<c<x, следовательно,
, где c1 между c0 и x0. По условию теоремы f ''(x) < 0. Определим знак произведения второго и третьего сомножителей. 1. Предположим, что x>x0. Тогда x0<c1<c<x, следовательно,  (x – x0) > 0 и (c – x0) > 0. Поэтому
(x – x0) > 0 и (c – x0) > 0. Поэтому 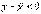 . 2. Пусть x<x0, следовательно, x < c < c1 < x0 и (x – x0) < 0, (c – x0) < 0. Поэтому вновь
. 2. Пусть x<x0, следовательно, x < c < c1 < x0 и (x – x0) < 0, (c – x0) < 0. Поэтому вновь 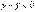 . Таким образом, любая точка кривой лежит ниже касательной к кривой при всех значениях x и x0 (a; b), а это значит, что кривая выпукла. Вторая часть теоремы доказывается аналогично. Точка графика непрерывной функции, отделяющая его выпуклую часть от вогнутой, называется точкой перегиба. Очевидно, что в точке перегиба касательная, если она существует, пересекает кривую, т.к. с одной стороны от этой точки кривая лежит под касательной, а с другой стороны – над нею.
. Таким образом, любая точка кривой лежит ниже касательной к кривой при всех значениях x и x0 (a; b), а это значит, что кривая выпукла. Вторая часть теоремы доказывается аналогично. Точка графика непрерывной функции, отделяющая его выпуклую часть от вогнутой, называется точкой перегиба. Очевидно, что в точке перегиба касательная, если она существует, пересекает кривую, т.к. с одной стороны от этой точки кривая лежит под касательной, а с другой стороны – над нею.  Определим достаточные условия того, что данная точка кривой является точкой перегиба.
Определим достаточные условия того, что данная точка кривой является точкой перегиба.  Теорема. Пусть кривая определяется уравнением y = f(x). Если f ''(x0) = 0 или f ''(x0) не существует и при переходе через значение x = x0 производная f ''(x) меняет знак, то точка графика функции с абсциссой x = x0 есть точка перегиба. Доказательство. Пусть f ''(x) < 0 при x < x0 и f ''(x) > 0 при x > x0. Тогда при x < x0 кривая выпукла, а при x > x0 – вогнута. Следовательно, точка A, лежащая на кривой, с абсциссой x0 есть точка перегиба. Аналогично можно рассматривать второй случай, когда f ''(x) > 0 при x < x0 и f ''(x) < 0 при x > x0. Таким образом, точки перегиба следует искать только среди таких точек, где вторая производная обращается в нуль или не существует.
Теорема. Пусть кривая определяется уравнением y = f(x). Если f ''(x0) = 0 или f ''(x0) не существует и при переходе через значение x = x0 производная f ''(x) меняет знак, то точка графика функции с абсциссой x = x0 есть точка перегиба. Доказательство. Пусть f ''(x) < 0 при x < x0 и f ''(x) > 0 при x > x0. Тогда при x < x0 кривая выпукла, а при x > x0 – вогнута. Следовательно, точка A, лежащая на кривой, с абсциссой x0 есть точка перегиба. Аналогично можно рассматривать второй случай, когда f ''(x) > 0 при x < x0 и f ''(x) < 0 при x > x0. Таким образом, точки перегиба следует искать только среди таких точек, где вторая производная обращается в нуль или не существует. 