Разрывы первого и второго рода.

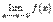Точка является точкой разрыва первого рода, если существуют конечные пределы и 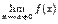, т.е. выполняется второе условие непрерывности и не выполняются остальные условия или хотя бы одно из них.

Точка является точкой разрыва второго рода, если один из пределов 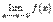и 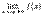равен бесконечности ( )

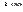Задача о производительности труда. Определение производной. Зависимость между непрерывностью и дифференцируемостью функции.

В выполнением (индивидуально или совместно) определённого объёма работы, используют формулу:

A=Wt,

где А -количество всей работы, намеченной к выполнению (по смыслу задачи часто А принимают за единицу), t -время выполнения всего количества работы, W - В сборнике Сканави об этом написано так: "При решении задач, связанных с производительность труда, т.е. количество работы, выполняемой за единицу времени."

Если весь объём работы, принятый за единицу, выполняется одним субъектом за t1, а вторым -за t2 единиц времени, то производительность труда при их совместном выполнении того же объёма работы равна: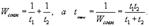

Как это применить на практике? Предлагаю рассмотреть на примерах решения задач.

Пример 1. Одна бригада может убрать поле за 12 дней. Другой бригаде для выполнения той же работы нужно 75% этого времени. После того как в течение 5 дней работала только первая бригада, к ней присоединилась вторая, и обе вместе закончили работу. Сколько дней работали бригады вместе?

Решение:t₁=12 дней.Так как t₂ равно 75% от времени работы первого, то: t₂=0,75*12=9 дней.

Производительность первой бригады равна:

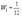Если первая бригада работала 5 дней, то она выполнила объём работы:

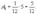Осталось выполнить:

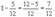
Когда подключилась вторая бригада, производительность стала:

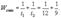
Пусть время их совместной работы равно х. Тогда получаем формулу для оставшейся части работы: 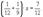Решаем полученное уравнение:

Значит, вместе бригады работали 3 дня.

Понятие производной

Рассмотрим задачу, которая приводит к понятию производной. Пусть функция u(t) выражает количество произведенной продукции за время t. Найдем производительность труда в момент t₀. За период от t₀ до t₀+Δ t количество продукции изменится от u(t₀) до u₀+Δ u = u(t₀+Δ t). Тогда средняя производительность труда за этот период z = Δ u/Δ t, поэтому производительность труда в момент t₀

z = lim_{D t® 0}D u/D t.

Определение 1 (производная).Производной функции y = f(x) в фиксированной точке x называется предел

lim_{D x® 0}D y/D x

при условии существования этого предела.

Производная обозначается следующим образом f'(x) или y'.

Определение 2.Правой (левой) производной называется правый (левый) предел

lim_{D x® 0 + 0}D y/D x lim_{D x® 0 - 0}D y/D x ,

если эти пределы существуют.

Для обозначения правой (левой) производной используют символ: f'(x+0) f'(x-0). Необходимым и достаточным условием существования производной является равенство f'(x+0) = f'(x-0).

Геометрический смысл производной

Рассмотрим график функции y = f(x), определенной и непрерывной на (a,b). Зафиксируем произвольную точку x на (a,b), и зададим приращение D x¹ 0, причем x+D x Î (a,b). Пусть точки M,P - точки на графике f(x), абсциссы которых равны x, x+D x (рис.21). Координаты точек M и P имеют вид M(x,f(x)), P(x+D x,f(x+D x). Прямую, проходящую через точки M, P графика функции f(x) будем называть секущей. Обозначим угол наклона секущей MP к оси ОX через f (D x). Определение 3.Если существует предельное положение секущей MP при стремлении точки N к точке M вдоль графика функции при D x® 0), то это предельное положение называется касательной к графику функции f(x) в данной точке M этого графика.

Из данного определения следует, что для существования касательной к графику f(x) в точке M достаточно, чтобы существовал предел lim_{D x® 0}f (D x) = f ₀, который равен углу, образованному касательной с положительным направлением оси OX. Справедливо утверждение:

Предложение 1.Если f(x) имеет в данной точке x производную, то существует касательная к графику функции f(x) в точке
M( x,f(x)) , причем угловой коэффициент этой касательной равен производной f'(x).

Из этого утверждения вытекает геометрический смысл производной: производная f'(x₀) есть угловой коэффициент касательной, проведенной к кривой y = f(x) в точке x₀, который в свою очередь равен tg угла наклона касательной к графику функции.

Тогда уравнение касательной к кривой f(x) в точке x₀ имеет вид

y = f(x₀)+f'(x₀)(x-x₀)

Определение 4 (дифференцируемость в точке).Функция f(x) называется дифференцируемой в точке x, если приращение D y этой функции в точке x представимо в виде

D y =AD x +a (D x) D x, (1)

где A - некоторое число, не зависящее от D x, а lim_{D x® 0} a (D x ) = 0.

В дальнейшем будем считать, что α(0) = 0. В этом случае функция Δ(x) будет непрерывной в точке Δ x = 0. Равенство 1 можно переписать иначе, так как функции Δ (Δ x), Δ x - бесконечно малые в точке Δ x = 0 и их произведение тоже бесконечно малая функция, поэтому

D y =AD x +o(D x).

(2)

Справедлива теорема

Теорема 1.Для того чтобы функция была дифференцируема в точке x, необходимо и достаточно, чтобы она имела в этой точке конечную производную.

Доказательство. Необходимость. Пусть функция дифференцируема, тогда ее приращение представимо в виде (1). Поделив (1) на Δ xΔ 0 получим

D y/D x = A+a(D x).

Переходя к пределу в последнем выражении при Δ x→ 0, получим, что A=f'(x).

Достаточность. Пусть существует конечная производная f'(x), то есть существует конечный предел

lim_{D x® 0}D y/D x = f'(x).

Обозначим α(Δ x) = Δ y/ Δ x-f'(x). Отсюда вытекает представление (1).

Теорема 2 (дифференцируемость и непрерывность).Если
функция дифференцируема в точке x, то она непрерывна в этой точке.

Доказательство. Так как функция дифференцируема в точке x, то то ее приращение представимо в виде (1), из которого следует, что lim_{D x® 0}D y = 0, что означает непрерывность функции в данной точке.

Заметим, что из непрерывности в данной точке не следует дифференцируемость в этой точке. Это видно из рассмотренного выше примера 4.

Производная непрерывной функции не обязательно непрерывна. Если функция имеет непрерывную производную на некотором множестве X, то функция называется гладкой на этом множестве. Если производная допускает конечное число точек разрыва (причем первого рода), то такая функция называется кусочно гладкой.