Бесконечно малые и бесконечно большие функций. Свойства.

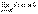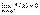Функция y=f(x) называется бесконечно малой при x→a или при x→∞, если или , т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.

Примеры.

1. Функция f(x)=(x-1)² является бесконечно малой при x→1, так как 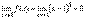(см. рис.).

2. Функция f(x) = tgx – бесконечно малая при x→0.

3. f(x) = ln (1+x)– бесконечно малая при x→0.

4. f(x) = 1/x– бесконечно малая при x→∞.

Установим следующее важное соотношение:

Теорема. Если функция y=f(x) представима при x→aв виде суммы постоянного числа b и бесконечно малой величины α(x): f (x)=b+ α(x) то .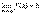

Обратно, если 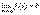, то f (x)=b+α(x), где a(x) – бесконечно малая при x→a.

Доказательство.

1. Докажем первую часть утверждения. Из равенства f(x)=b+α(x) следует |f(x) – b|=| α|. Но так как a(x) – бесконечно малая, то при произвольном ε найдется δ – окрестность точки a, при всех x из которой, значения a(x) удовлетворяют соотношению |α(x)|<ε. Тогда |f(x) – b|< ε. А это и значит, что .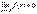

2. Если 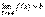, то при любом ε>0 для всех х из некоторой δ – окрестность точки a будет |f(x) – b|< ε. Но если обозначимf(x) – b= α, то |α(x)|<ε, а это значит, что a – бесконечно малая.

Рассмотрим основные свойства бесконечно малых функций.

Теорема 1. Алгебраическая сумма двух, трех и вообще любого конечного числа бесконечно малых есть функция бесконечно малая.

Доказательство. Приведем доказательство для двух слагаемых. Пусть f(x)=α(x)+β(x), где 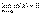и 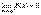. Нам нужно доказать, что при произвольном как угодно малом ε>0 найдется δ>0, такое, что для x, удовлетворяющих неравенству |x – a|<δ, выполняется |f(x)|< ε.

Итак, зафиксируем произвольное число ε>0. Так как по условию теоремы α(x) – бесконечно малая функция, то найдется такое δ₁>0, что при |x – a|<δ₁ имеем |α(x)|< ε/2. Аналогично, так как β(x) – бесконечно малая, то найдется такое δ₂>0, что при |x – a|<δ₂ имеем | β(x)|< ε/2.

Возьмем δ=min{ δ₁, δ₂}.Тогда в окрестности точки a радиуса δбудет выполняться каждое из неравенств |α(x)|< ε/2 и | β(x)|< ε/2. Следовательно, в этой окрестности будет

|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)| < ε/2 + ε/2= ε,

т.е. |f(x)|<ε, что и требовалось доказать.

Теорема 2. Произведение бесконечно малой функции a(x) на ограниченную функцию f(x) при x→a (или при x→∞) есть бесконечно малая функция.

Доказательство. Так как функция f(x) ограничена, то существует число М такое, что при всех значениях x из некоторой окрестности точки a|f(x)|≤M. Кроме того, так как a(x) – бесконечно малая функция при x→a, то для произвольного ε>0 найдется окрестность точки a, в которой будет выполняться неравенство |α(x)|< ε/M. Тогда в меньшей из этих окрестностей имеем | αf|< ε/M= ε. А это и значит, что af – бесконечно малая. Для случая x→∞ доказательство проводится аналогично.

Из доказанной теоремы вытекают:

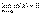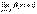Следствие 1. Если и , то .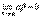

Следствие 2. Если 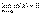и c=const, то .

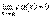Теорема 3. Отношение бесконечно малой функции α(x) на функцию f(x), предел которой отличен от нуля, есть бесконечно малая функция.

Доказательство. Пусть 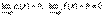. Тогда 1/f(x) есть ограниченная функция. Поэтому дробь 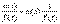есть произведение бесконечно малой функции на функцию ограниченную, т.е. функция бесконечно малая.

Во всех приведённых ниже формулах бесконечность справа от равенства подразумевается определённого знака (либо «плюс», либо «минус»). То есть, например, функция xsinx, неограниченная с обеих сторон, не является бесконечно большой при .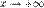

Последовательность a_n называется бесконечно большой, если .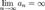

Функция называется бесконечно большой в окрестности точки x₀, если .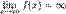

Функция называется бесконечно большой на бесконечности, если 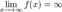либо .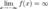

Свойства бесконечно малых

· Сумма конечного числа бесконечно малых — бесконечно малая.

· Произведение бесконечно малых — бесконечно малая.

· Произведение бесконечно малой последовательности на ограниченную — бесконечно малая. Как следствие, произведение бесконечно малой на константу — бесконечно малая.

· Если a_n — бесконечно малая последовательность, сохраняющая знак, то 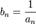— бесконечно большая последовательность.

Сравнение бесконечно малых.

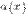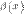Пусть и — бесконечно малые при .
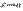1. Если 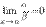, то говорят, что 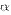является бесконечно малой высшего порядка по сравнению с 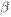. В этом случае пишут .
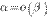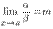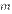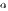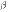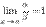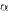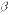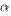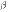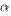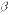2. Если , где —число, отличное от нуля, то говорят, что и — бесконечно малые одного и того же порядка. В частности, если , то бесконечно малые и называются эквивалентными. Запись ~ означает, что и —эквивалентные бесконечно малые. Если 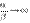, то это означает, что 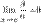. Таким образом, 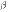является бесконечно малой высшего порядка по сравнению с 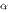, т. е.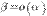
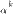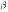3. Если и —бесконечно малые одного и того же порядка, причем 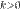, то говорят, что бесконечно малая 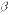имеет порядок 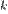по сравнению с .
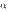Отметим некоторые свойства бесконечно малых величин:
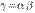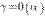1^o. Произведение двух бесконечно малых есть бесконечно малая высшего порядка по сравнению с сомножителями, т. е. если , то и .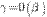
2^o. Бесконечно малые 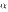и 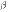эквивалентны тогда и только тогда, когда их разность 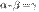является бесконечно малой высшего порядка по сравнению с 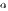и 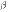, т. е. если , .
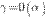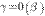3^o. Если отношение двух бесконечно малых имеет предел, то этот предел не изменится при замене каждой из бесконечно малых эквивалентной ей бесконечно малой, т.е. если
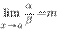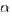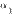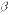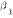, ~ , ~ , то .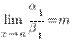

Полезно иметь в виду эквивалентность следующих бесконечно малых величин: если 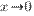, то

~ ~ ~ ~

~ ~

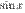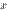
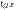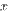
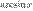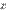
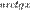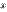
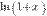
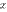
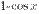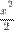
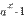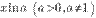
20. Непрерывность функций в точке. Точки разрыва.Представление о непрерывности функции интуитивно связано у нас с тем, что её графиком является плавная, нигде не прерывающаяся линия. При рассмотрении графика такой функции y = f(x) мы видим, что близким значениям аргумента соответствуют близкие значения функции : если независимая переменная приближается к точке x₀, то значение функции y = f(x) неограниченно приближается к значению функции в точкеx₀, т.е. к f(x₀).

Дадим строгое определение непрерывности функции . Итак, пусть имеем функцию y = f(x).

Функция y = f(x) называется непрерывной в точке x₀, если она определена в этой точке и в некоторой окрестности содержащей x₀ и 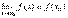Таким образом, можно сказать, что функция непрерывна в точкеx₀, если выполнены 3 условия:

1. она определена в точке x₀ и в некоторой её окрестности;

2. имеет предел при x → x₀;

3. этот предел равен значению функции в точке x₀.

Формулу (1) можно записать в виде 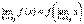, т.к. 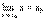. Это означает, что для того, чтобы найти предел непрерывной функции при x → x₀, достаточно в выражение функции подставить вместо аргументах его значение x₀.

Непрерывные функции обладают следующими свойствами.

Теорема 1. Если функции f(x) и g(x) непрерывны в точке x₀, то их сумма φ(x) = f(x) + g(x) также есть непрерывная функция в точке x₀.

Доказательство. Так как функции f(x) и g(x) непрерывны в точке x₀, то исходя из определения можно написать 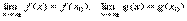. Тогда на основании свойств пределов будем иметь

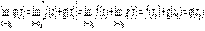.Эта теорема справедлива для любого конечного числа слагаемых.

Следующие две теоремы докажите самостоятельно аналогично теореме 1.

Теорема 2. Произведение двух непрерывных функций есть функция непрерывная.

Теорема 3. Частное двух непрерывных функций есть функция непрерывная, если знаменатель в рассматриваемой точке не обращается в нуль.

Если функцию можно представить в виде y = f(u), где u =φ(x), т.е. если функция зависит от переменной через промежуточный аргумент u, то называется сложной функцией переменной x.

Справедлива следующая теорема.

Теорема 4. Если функция u = φ(x) непрерывна в точкеx₀ и принимает в этой точке значение u₀ = φ(x₀), а функция f(u) непрерывна в точке u₀, то сложная функция y = f(φ(x)) непрерывна в точке x₀.

Используя эти теоремы можно доказать следующий результат.

Теорема 5. Всякая элементарная функция непрерывна в каждой точке , в которой она определена.

Заметим, что если функция y = f(x) непрерывна в точке x₀ и её значение в этой точке отлично от 0, f(x₀) ≠ 0, то значения функции f(x) в некоторой окрестности точки x₀ имеют тот же знак, что и f(x₀), т.е. если f(x₀) > 0, то найдётся такое δ > 0, что на интервале(x₀– δ;x₀+ δ) f(x) > 0 (в этой окрестности значения функции f(x) очень мало отличаются от своего предела).Определение. Функция 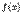имеет точку разрыва при 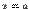, если она определена слева и справа от точки 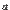, но в точке 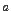не выполняется хотя бы одно из условий непрерывности.

Точки разрыва функции :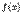

1. Точка устранимого разрыва;

2. Точка разрыва первого рода;

3. Точка разрыва второго рода.

Точка является точкой устранимого разрыва, если функция в точке 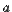не определена и существуют равные конечные пределы 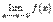и 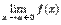, т.е. .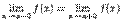