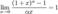Предел функций в точке. Арифметические операций над пределами.

Преде́л фу́нкции (предельное значение функции) —значение, к которому функция в определённом смысле приближается при приближении аргумента к определённой точке.

Определение предела по Коши. Число A называется пределом функции f (x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для каждого ε > 0 существует δ > 0 такое, что для всех x, удовлетворяющих условию |x – a| < δ, x ≠ a, выполняется неравенство |f (x) – A| < ε.

Определение предела по Гейне. Число A называется пределом функции f (x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для любой последовательности 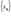такой, что 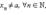сходящейся к числу a, соответствующая последовательность значений функции 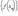сходится к числу A.

Если функция f (x) имеет предел в точке a, то этот предел единственный.

Число 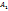называется пределом функции f (x) слева в точке a, если для каждого ε > 0 существует δ > 0 такое, что для всех 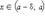выполняется неравенство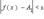

Число 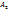называется пределом функции f (x) справа в точке a, если для каждого ε > 0 существует δ > 0 такое, что для всех 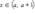выполняется неравенство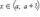

Предел слева обозначается 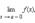предел справа – 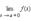Эти пределы характеризуют поведение функции слева и справа от точки a. Их часто называют односторонними пределами. В обозначении односторонних пределов при x → 0 обычно опускают первый нуль: 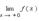и .

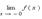Арифметические операции над пределами

Везде в этом пункте рассматриваются конечные пределы.

1) 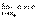, , 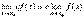если .

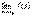2) 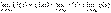, если существуют конечные пределы , .

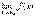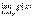3) 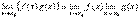, если существуют конечные пределы , .

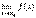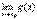Следствие: 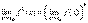, если существует конечный предел .

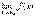4)  

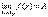
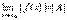
5) g(x)0, ,  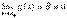

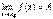
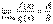
Замечание: Аналогичные свойства имеют место для односторонних пределов

17. Два замечательных предела и их следствия. Замеча́тельные преде́лы — термин, использующийся в советских и российских учебниках по математическому анализу для обозначения некоторых широко известных математических тождеств со взятием предела. Особенно известны:

· Первый замечательный предел: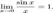

· Второй замечательный предел: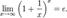

Первый замечательный предел

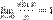
Доказательство

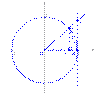Рассмотрим односторонние пределы 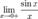и 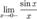и докажем, что они равны 1.

Пусть 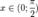. Отложим этот угол на единичной окружности (R = 1).

Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке (1;0). Точка H — проекция точки K на ось OX.

Очевидно, что:

(где S_sectOKA — площадь сектора OKA)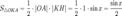

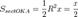
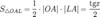(из : | LA | = tgx)

Подставляя в (1), получим: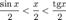

Так как при :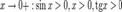

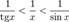Умножаем на sinx: 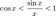Перейдём к пределу: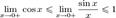

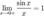
Найдём левый односторонний предел:

Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1.

Следствия

·

·

·

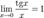
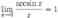
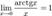
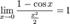· Доказательство следствий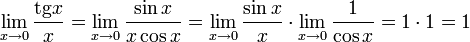

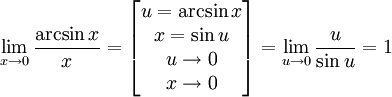
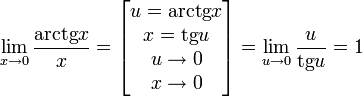
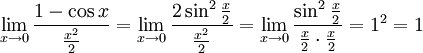
Второй замечательный предел

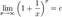Доказательство второго замечательного предела:

Доказательство для натуральных значений x 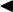Докажем вначале теорему для случая последовательности 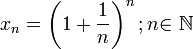По формуле бинома Ньютона: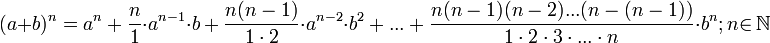

Полагая 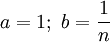, получим:

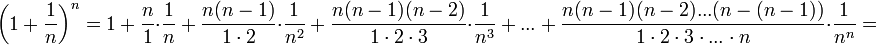
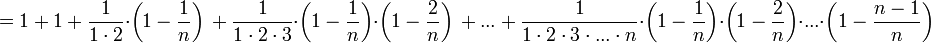(1)

Из данного равенства (1) следует, что с увеличением n число положительных слагаемых в правой части увеличивается. Кроме того, при увеличении n число убывает, поэтому величины 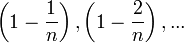возрастают. Поэтому последовательность 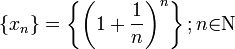— возрастающая, при этом

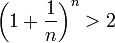(2).

Покажем, что она ограничена. Заменим каждую скобку в правой части равенства на единицу, правая часть увеличится, получим неравенство

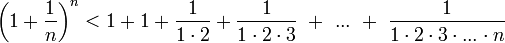
Усилим полученное неравенство, заменим 3,4,5, …, стоящие в знаменателях дробей, числом 2:

.

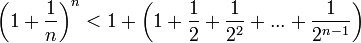Сумму в скобке найдём по формуле суммы членов геометрической прогрессии:

.

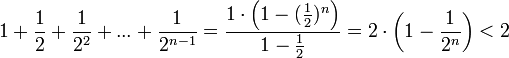Поэтому 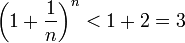(3).

Итак, последовательность ограничена сверху, при этом 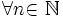выполняются неравенства (2) и (3): .

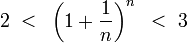Следовательно, на основании теоремы Вейерштрасса (критерий сходимости последовательности) последовательность 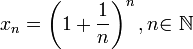монотонно возрастает и ограниченна, значит имеет предел, обозначаемый буквой e. Т.е.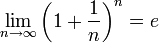

Зная, что второй замечательный предел верен для натуральных значений x, докажем второй замечательный предел для вещественных x, то есть докажем, что 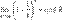. Рассмотрим два случая:

1. Пусть . Каждое значение x заключено между двумя положительными целыми числами: , где — это целая часть x.

Отсюда следует: 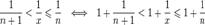, поэтому 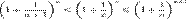.Если , то . Поэтому, согласно пределу 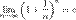, имеем:

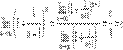
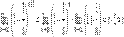.По признаку (о пределе промежуточной функции) существования пределов .

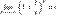2.Пусть 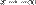. Сделаем подстановку − x = t, тогда

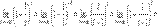
3. 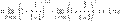.Из двух этих случаев вытекает, что 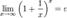для вещественного x.

Следствия

1.

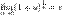
2.

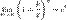
3.

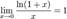
4.

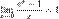
5. 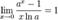для ,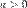

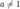
6.