Закон больших чисел. Неравенство Чебышева. Теорема Чебышева. Теорема Бернулли.
Закон больших чисел.Под законом больших чисел понимают общий принцип, в силу которого совместное действие случайных факторов приводит при определенных общих условиях к результату почти независящему от случая. Этот принцип выражается рядом теорем, которые основываются на неравенстве Чебышева.
Неравенство Чебышева.Вероятность того, что модуль отклонения случайной величины X от ее математического ожидания меньше любого положительного *E* и ровна или больше разности 1-D(x)/E2
P(Ix-M(x)I<E)=> 1-D(x)/E2
Теорема Чебышева.Случайные величины принимаютзначения, зависящие от многих причин, учесть которые не представляется возможности. Поведение суммы достаточно большого числа случ. величин при некоторых условиях утрачивают случ. характер и становятся законом.
Если случ. величины x1,x2,…xnнезависимы имеет математ. ожидание и дисперсии ,каждая из которых ограничена одним и тем же числом С, то для любого положительного числа Е выполняется неравенство:
P(│1∕n∑Xk - 1∕n∑M(Xk)│<E│)≥1-C∕n*E2 ,при к= от 1 до n
Введем понятие сходимости по вероятности. Случ.величиныx1....xn сходятся по вероятности к случайной величине Х,если для любого числаЕ выполняются:
LimP(│xn-x│<E)=1
n->∞
Следствие 1:если Случ.величиныx1....xn удовлетворяют условиям теоремы Чебышева, то:
LimP(│1∕n∑Xk - 1∕n∑M(Xk)│<E)=1
n->∞
т.е. среднее арифметическоезначение случ. величин сходится по вероятности к среднему арифметическому их мат.ожиданий.
Теорема Чебышева верна для дискретных и непрерывных случ. величин.
Следствие2:среднее арефмитическое последовательности попарно независимых величин, дисперсии которых равномерно ограничены и которые имеют одно и тоже мат. ожидание. М(хк)=а,к от 1 до n сходятся по вероятности по мат.ожиданию к а , если Е-любое положит.число.
LimP(│1∕n∑Xk - а│<E)=1
n->∞
Теорема Бернулли.Если m-число появлений события а в n-независимых испытанияхи p-вероятность появления события а в каждых испытаниях, то при достаточно больших n близка вероятность того,что модуль отклонения относит.величин меньше любого Е,но>0
LimP(│m∕n-p│<E)=1
41. Понятие о центральной предельной теореме.Теорема Ляпунова.Локальная теорема Лапласа.Интегральная теорема Лапласа.
Многие задачи теории вероятности связаны с изучением суммы независимых величин,которые при определенных условиях имеют распределение близкое к нормальному.
Теорема Ляпунова.Если х1…хn независимые случ величины имеющие одно и тоже распределение с математическим ожиданием а и дисперсией δ2=D(х)то при неограниченном возрастании n закон распределения суммы неограниченно приближается к нормальному при nнеогранич.возрастающ.
Локальная теорема Лапласа.если вероятность появления события а в каждом из nнезависимых испытаний ровна одной и той же р(0<p<1),то Рк,nтого,что во всех этих испытаниях событие а появится к разприближенно выражается формулой:
Рк,n= 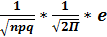 -(k-np)2/2npq
-(k-np)2/2npq
Рк,n= 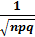 *φ(x)
*φ(x)
x = 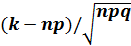
φ(x)= 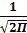 *
* 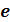 -x2/2
-x2/2
Интегральная теорема Лапласа.Если вероятность события а в каждом изn-независимых испытании ровна р,0<p<1 то Рк,n(к1,к2) того что в этих испытаниях событие а появится не менее к1 раз и не более к2 раз.Приближенно определяется формулой Рк,n(к1,к2)= 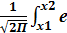 -х2/2dx
-х2/2dx
x1=-(k1-np)/ 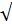 npq
npq
x2=(k2-np)/ 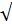 npq
npq
В этом соотношении Рn(к1,к2)= ф(х2)-ф(х1)
ф(х)-функция Лапласа из таблиц.
42.Векторные случайные величины.Закон распределения двумерной случ.величины.Функция распределения вероятностей двумерной случайной величины.
Векторные случайные величины.На ряду с одномерными рассматриваются еще и многомерные случвеличины.Это векторы ,координаты которых явл однородными случвеличинами.Это векторные величины.
х =(х1(ω), х2(ω)… хn(ω))
вектор х(ω) геометрически интерпретируется как случайная точка в пространстве Rnкоторая зависит от элементарного события.Закон распределения двумерной случ.величины.Закон распределения дискретной двумерной случайной величины (Х, Y) имеет вид таблицы с двойным входом, задающей перечень возможных значений каждой компоненты и вероятности p(xi, yj), с которыми величина принимает значение (xi, yj):
| Y | Х | |||||
| x1 | x2 | … | xi | … | xn | |
| y1 | p(x1, y1) | p(x2, y1) | … | p(xi, y1) | … | p(xn, y1) |
| … | … | … | … | … | … | … |
| yj | p(x1, yj) | p(x2, yj) | … | p(xi, yj) | … | p(xn, yj) |
| … | … | … | … | … | … | … |
| ym | p(x1, ym) | p(x2, ym) | … | p(xi, ym) | … | p(xn, ym) |
При этом сумма вероятностей, стоящих во всех клетках таблицы, равна 1.
Зная закон распределения двумерной случайной величины, можно найти законы распреде-ления ее составляющих. Действительно, событие Х = х1 представляется собой сумму несовместных событий (X = x1, Y = y1), (X = x1, Y = y2),…, (X = x1, Y = ym), поэтому
р(Х = х1) = p(x1, y1) + p(x1, y2) +…+ p(x1, ym) (в правой части находится сумма вероятностей, стоящих в столбце, соответствующем Х = х1). Так же можно найти вероятности остальных возможных значений Х. Для определения вероятностей возможных значений Y нужно сложить вероятности, стоящие в строке таблицы, соответствующей Y = yj. Пример 1. Дан закон распределения двумерной случайной величины:
| Y | X | ||
| -2 | |||
| -0,8 | 0,1 | 0,3 | 0,1 |
| -0,5 | 0,15 | 0,25 | 0,1 |
Найти законы распределения составляющих.
Решение. Складывая стоящие в таблице вероятности «по столбцам», получим ряд распре-деления для Х:
| Х | -2 | ||
| р | 0,25 | 0,55 | 0,2 |
Складывая те же вероятности «по строкам», найдем ряд распределения для Y:
| Y | -0,8 | -0,5 |
| p | 0,5 | 0,5 |
Функция распределения вероятностей двумерной случайной величины. Функцией распределения F(x, y)двумерной случайной величины (X, Y) называется вероятность того, что X < x, a Y < y: F( х, у ) = p ( X < x, Y < y ). Замечание. Определение функции распределения справедливо как для непрерывной, так и для дискретной двумерной случайной величины.
Свойства функции распределения.
1) 0 ≤ F(x, y) ≤ 1 (так как F(x, y) является вероятностью).
2) F(x, y) есть неубывающая функция по каждому аргументу:
F(x2, y) ≥ F(x1, y), если x2>x1;
F(x, y2) ≥ F(x, y1), если y2>y1.
Доказательство. F(x2, y) = p(X < x2, Y < y) = p(X < x1, Y < y) + p(x1 ≤ X < x2, Y < y) ≥
≥ p(X < x1, Y < y) = F(x1, y). Аналогично доказывается и второе утверждение.
3) Имеют место предельные соотношения:
а) F(-∞, y) = 0; b) F(x, - ∞) = 0; c) F(- ∞, -∞) = 0; d) F( ∞, ∞) = 1.
Доказательство. События а), b) и с) невозможны ( так как невозможно событие Х<- ∞ или Y <- ∞), а событие d) достоверно, откуда следует справедливость приведенных равенств.
4) Приу = ∞ функция распределения двумерной случайной величины становится функцией распределения составляющей Х:
F(x, ∞) = F1(x).
При х = ∞ функция распределения двумерной случайной величины становится функцией распределения составляющей Y :
F( ∞, y) = F2(y).
Доказательство. Так как событие Y <∞ достоверно, то F(x, ∞) = р(Х < x) = F1(x). Аналогично доказывается второе утверждение.




