Предел функции в точке, непрерывность ф.м.п.

Пусть функция z=f(x;y) определена в некоторой окрестности точки Мо(Xо;Yо), кроме, быть может, самой этой точки. Число А называется пределом функции z=f(x;y) при х→Xо и у→Yо (или, что то же самое, при М(х;у)→Мо(Xо;Yо)), если для любого ε> 0 существует > 0 такое, что для всех х Xо и у у₀ и удовлетворяю­щих неравенству < выполняется неравенство <ε. Записывают:

или

Функция z = f(x;у) (или f(М)) называется непрерывной в точ­ке Мо(хо;уо), если она:

а)определена в этой точке и некоторой ее окрестности,

б)имеет предел ,

в) этот предел равен значению функции z в точке М₀, т. е.

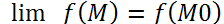
Функция z = f(x;у) называется непрерывной в точке М₀(X₀;Y₀) D, если выполняется равенство ,т. е. полное приращение функции в этой точке стремится к нулю, когда приращения ее аргументов x и у стремятся к нулю.

Локальные экстремумы ф.м.п.

Точка (хо;уо) называется точкой максимума функции z = f(х;у), если существует такая -окрестность точки (Xо; Yо), что для каждой точки (x; у), отличной от (хо;уо), из этой окрестности вы­полняется неравенство f(x; у) < f(Xо;Yо).Аналогично определяется точ­ка минимума функции: для всех точек (x; у), отличных от (Xо;Yо), из -окрестности точки (Xо;Yо) вы­полняется неравенство: f(x;у) >f(Xо;Уо).Значение функции в точке мак­симума (минимума) называется максимумом (минимумом) функции. Максимум и минимум функ­ции называют ее экстремумами.

Необходимое условие существования экстремума

Если в точке N(хо;уо) дифференцируемая функция z=f(х;у) имеет экстремум, то ее частные производные в этой точке равны нулю: f’_х(хо;уо)=0,

f’y(х₀;уо)=0.

Достаточные условия существования экстремума

Пусть в стаци­онарной точке (хо;уо) и некоторой ее окрестности функция f(x;у) имеет непрерывные частные производные до второго порядка вклю­чительно. Вычислим в точке (х₀;у₀) значения А=f"_хx(хо;уо), В= 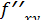(Xо;Уо), С= 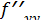(х₀;у₀).

Обозначим 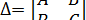=AC-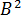

Тогда:

1) если >0, то функция f(x;у) в точке (Xо;Yо) имеет экстремум: максимум, если А < 0; минимум, если А > 0;

2)если <0, то функция f(x;у) в точке (Xо;Yо) экстремума не имеет. В случае =0 экстремум в точке (Xо;Yо) может быть, может не быть.

Исследование функции на монотонность

Функция f называется неубывающей (невозрастающей) на интервале (а,в),если для 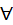х1,х2 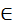(а,в) из неравенства х1<х2 следует f(x1) 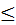f(x2) (f(x1) 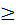f(x2)). При этом функция f возрастает (убывает), если f(x1) 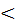f(x2) (f(x1) 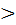f(x2)) при х1<x2 на (а,в). Возрастающие или убывающие на интервале (а,в) функции называются монотонными на этом интервале.

Решение ДУ 1-го порядка с разделяющимися переменными.

Уравнение с разделяющимися переменными может быть записано в симметрической форме М(х)N(y)dx+P(x)Q(y)dy=0,где M,N,P,Q – интервалы в a<x<b, c<y<d. Общий интеграл: 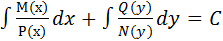если Р(х) 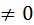, N(y) 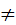0. Если N(y)=0, c<y<d, то y=y’ – решение, не входящее в общий интеграл. Если P(x1)=0, a<x1<b, то х=х1- решение.

Дифференцируемость ф.м.п. Примеры применения частных производных в экономике.

Функция f(x, y) дифференцируема в точке (x0, y0) (или сокращенно 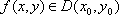), если справедливо равенство:

(1) f(x, y)=f(x0, y0) + A(x - x0) + B(y - y0) +0(p) где 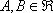- некоторые константы, а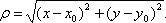

Зафиксируем одну из переменных, например: y=y0. Тогда f(x0, y0) будет функцией от x и равенство (1) примет вид: f(x0, y)=f(x0, y0) + A(x - x0) + B(y - y0) + o(x - x0). Следовательно, число A есть производная функции f(x0, y) в точке x=x0. Эта производная обозначается так: 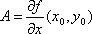и называется частной производной f(x, y) по x в точке (x0, y0). Аналогично: 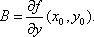Таким образом условие дифференцируемости функции f(x, y) в точке (x0, y0) можно представить в виде:

f(x, y)=f(x0, y0) + 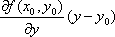+0(p). В экономических исследованиях часто используется производственная функция Кобба-Дугласа 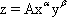, где z - величина общественного продукта, x - затраты труда, y - объем производственных фондов (обычно z и y измеряются в стоимостных единицах, x - в человеко-часах); A, a, b - постоянные.

Применение в экономическом анализе. Базовой задач экон анализа явл изучение связей эконом величин, записан в виде функй.

В экон-ке очень часто требуется найти наил или оптим значение показателя: наив производ-ть труда, макс прибыль, макс выпуск, мин издержки и т. д. Каждый показатель представляет собой функ от одного или неск-х аргументов.