Матрицы. Сложение матриц и умножение на число.Их свойства.

Матрицы. Сложение матриц и умножение на число.Их свойства.

Пусть m,n- целые положительные числа и M- непустое множество элементов любой природы. Матрицейразмеров m*n над М или m*n –матрицей над M называется прям.таблица,составленная из mnэлементов множества М и содержащаяm строк и n столбцов.

Пусть A=(а_i,j)_m*n и B=(b_i,j)_m*n две матрицы одинаковой размерности,сумма матриц A и B, называется матрица такой же размерности, у которой каждый элемент равен сумме элементов A и B.

Произведение матрицы A=(а_i,j)_m*n на число С( С? R),называется m*n – матрица такой же размерности, у которой каждый элемент равен произведению соотв. элемента матрицы A на число С.

1. A+B=B+A(коммунативность сложения)

2. (A+B)+C=A+(B+C)(ассоциативность)

3. A+0=A

4. A+(-A)=0

5. α(A+B)=αA+αB

6. (α+β)A=αA+βB

7. (αβ)A=α(βA)

8. 1*A=A

Умножение матриц, его свойства.

Пусть даны матрица A=(а_i,j)_m*nи B=(b_i,j)_n*r, у кот.число элементов в строке первой матрицы равно числу элементов в столбце второй матрицы.

Произведением матрицы А на матрицу В наз. матрица С (С=А*В=АВ) размерности m*r, у кот. каждый эл-т равен сумме произведений эл-ов соответствующих строки и столбца матриц А и В.

Свойства:

1)АВ≠ВА-умножение матриц некоммутатитвно;

2)(АВ)*С=А*(ВС)-умножение матриц ассоциативно;

3)А*(В+С)=АВ+АС

(В+С)*А=ВА+СА-умножение матриц дистрибутивно по отношению к сложению;

4)α(АВ)=(αА)В=А(αВ);

Системы ур-ний. Матричная запись системы ур-ний.Связь между решение матричногоур-ния и решением системы.

Системы линейных однородных уравнений

Уравнение называется линейным, если оно содержит неизвестные в первой степени. Так, например, 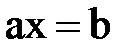есть линейное уравнение с одним неизвестным; 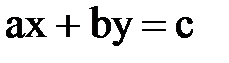- линейное уравнение с двумя неизвестными.

Если в исходной системе все свободные члены равны нулю, то система называется однородный. Такая система всегда совместна, так как она имеет нулевое решение: .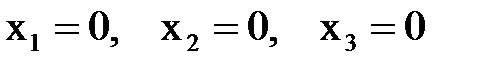

Система называется совместной, если она имеет хотя бы одно решение: 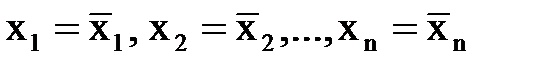, и несовместной, если она не имеет ни одного решения. Если система совместна и имеет единственное решение, то она называется определенной; если же решений бесконечно много, то система называется неопределенной. При работе с системой принципиальным является вопрос о ее совместности. Пусть доказано, что система совместна. Возможны следующие случаи:

а) если система совместна, то есть 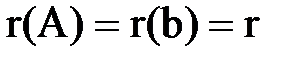и число неизвестных равно рангу матриц А и В 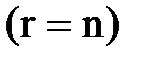, то она имеет единственное решение;

б) если же система совместна, но 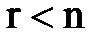, то она имеет бесконечно много решений.

Теорема Кронекера-Капелли:Для совместности системы линейных уравнений необходимо и достаточно, что бы ранг матрицы системы был равен рангу расширенной матрицы.

ФормулыКрамера.

Рассмотрим частный случай системы (4), когда число уравнений совпадает с числом неизвестных. Пусть для определенности 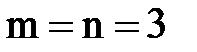, то есть система имеет вид

.

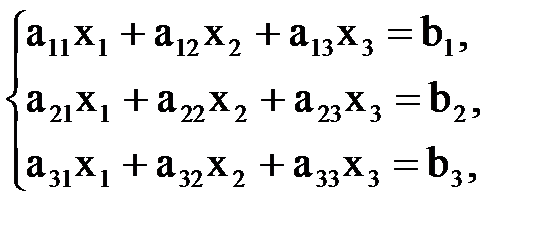
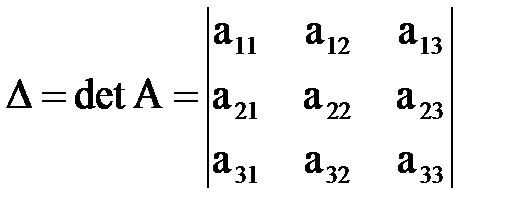Определитель называется основным определителем данной системы. Следующие три определителя называются вспомогательными:

, , .

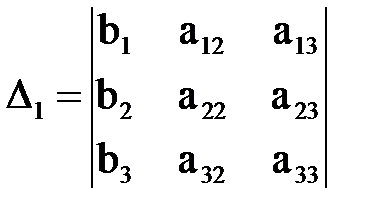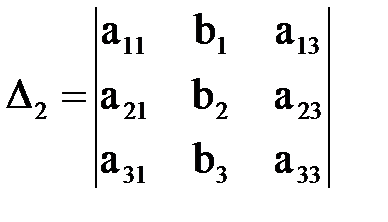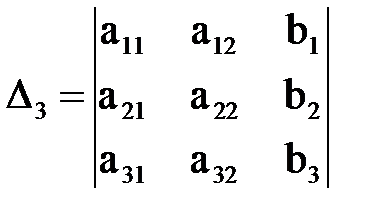Теорема Крамера:Если определитель матрицы А 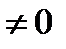то система имеет единственное решение определяющееся формулами: .

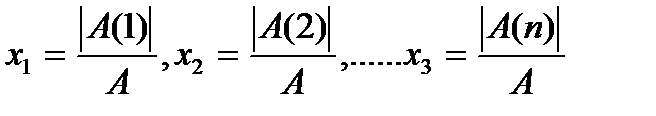Доказательство:

АХ=B.не трудно показать что матрица Х= 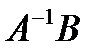является решением данного уравнения ( 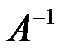существует т.к.определитель матрицы А 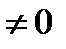).Действительно А( 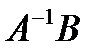)=В; ( 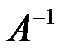А)В=В; ЕВ=В; В=В.Верно.Покажем, что данное математическое уравнение имеет единственное решение.Пусть 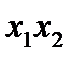решение данного уравнения, тогда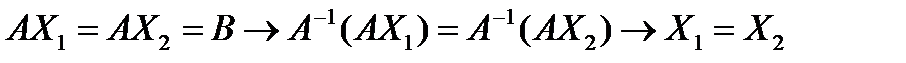

АХ=В определяется формулой Х= 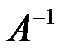В. То есть = ==

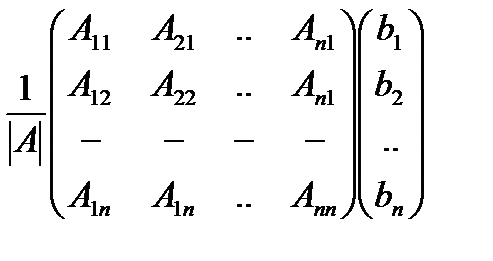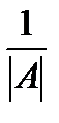
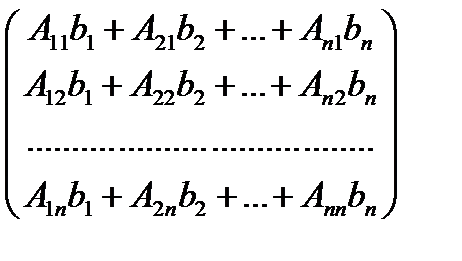
Заметим что определитель матрицы А(1);

А(1)=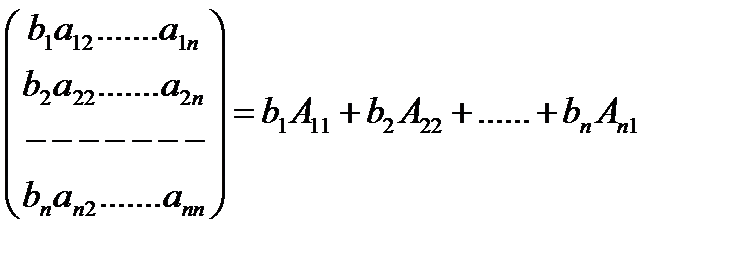

А(2)=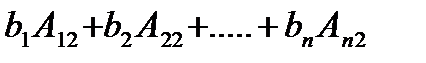

- - - - - - - - - - - -- - - - - - - -

А(3)=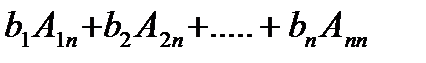

Алгебраические дополнения последних формулах составлены к матрицам отличных от А, но при их нахождении столбик свободных членов вычеркивается, поэтому они совпадают с соответств. алгебраич. дополнением матрицы А.Таким образом: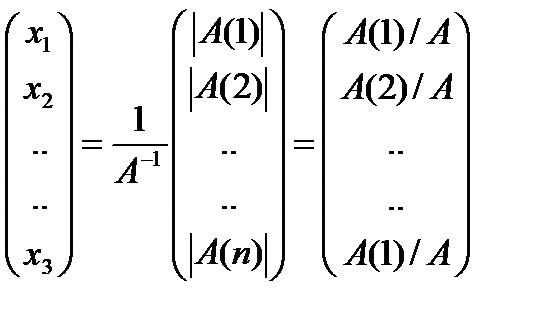

Замечание: При доказательстве теоремы 5 мы получили попутно способ решения систем с помощью обратной матрицы, его удобно применять если обратная матрица, матрица систем известна.

Метод Гаусса

Метод Гаусса –решение СЛУ в последовательном исключении неизвестных .

Замечание1-при решениисист. Методом Гауса работают только со строками расширенной матрицы.

Существует общий метод решения системы из 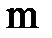уравнений с 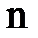неизвестными, который называется методом последовательного исключения неизвестных или методом Гаусса.Последовательное исключение неизвестных проще и короче проводить с помощью элементарных преобразований расширенной матрицы данной системы. К ним относятся:

а) перестановка местами каких-либо строк матрицы;

б) умножение или деление (сокращение) какой-либо строки матрицы на число, отличное от нуля;

в) умножение какой-либо строки матрицы на число 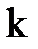и прибавление к другой строке.

Очевидно, что элементарные преобразования не изменяют ранга расширенной матрицы, другими словами, не нарушают равносильности исходной системы. После ряда таких преобразований исходная матрица будет приведена к одному из следующих видов:

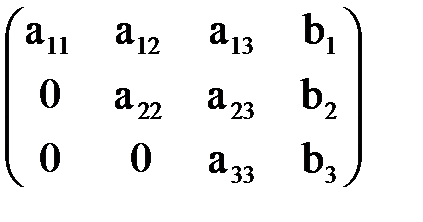или .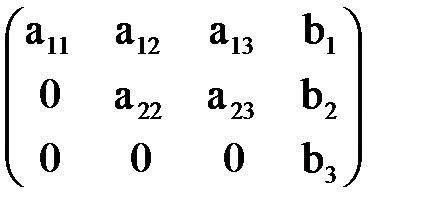

В первом случае система имеет единственное решение, во втором – либо бесконечно много решений, если 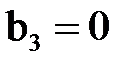, либо не имеет решений, если .

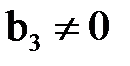Векторное пространство. Примеры.

Мн-во М наз. векторным (линейным) пространством, а его эл-ты векторами, если:

I.Задан закон (операция сложения) по кот. кажд. паре векторов 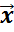, 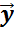?Mсопоставляется единственный вектор изМ,наз. их суммой и обозн. + ;

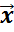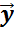II.Задан закон (операция умножения на число) по кот. каждому вектору 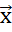? Ми числу α ? Rставится в соответствие единственный вектор, наз. произведение вектора на число и обознач. .

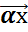III.Для любых векторов 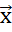, , 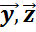?Mи любых α, β ? М справедливы след. равенства:

1) + = + ;

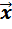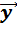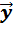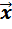2) ( + )+ = +( + );

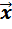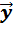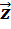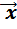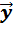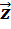3) Существует такой элемент 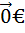М, что + = + = ;

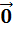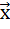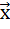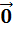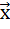4) Существует эл-т –х ? М ,что – + = +(- )= ;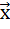

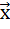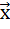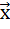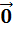5) ( + ) = + ;

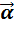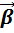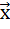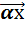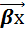6) ( + )= + ;

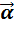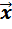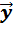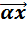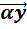7) 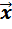(αβ) =α(β );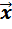

8) 1*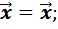

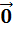– наз. нулевым, а вектор – 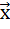– противоположным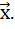

Пример1. Множество всех m*n матриц, по отношению к операциям сложения матриц и умножения матриц на число явл. векторным пространством.

Пример2.Множество всех векторов на плоскости (в пространстве) с обычными операциями сложения векторов и умножения вектора на число явл. векторным пространством.

Прямая на плоскости.

Определение. Любая прямая на плоскости может быть задана уравнением первого порядка

Ах + Ву + С = 0 илиА(х-х₀)+ В(у-у₀)=0

причем постоянные А, В не равны нулю одновременно, т.е. А² + В²¹ 0. Это уравнение первого порядка называют общим уравнением прямой.

Заметим, что ненулевой вектор параллельной прямой наз. направляющим.

Вектор, перпендикулярный прямой наз. нормальным вектором прямой.

Пусть М (х₀;у₀) ? l, тогда 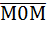ǁ 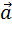=> 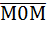(х-х₀ ; у-у₀) ǁ 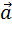(m;n) =>

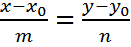– каноническое уравнение прямой ;

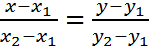– уравнение прямой, проход.через 2 точки;

d 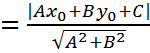– расстояние от точки до прямой ;

у= kx+b– уравнение прямой по угловому коэффиценту ;

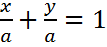– уравнение прямой в отрезках по осям ;

Взаимное расположение прямых на плоскости:

l₁: A₁x+B₁y+C₁=0

l₂:A₂x+B₂y+C₂=0

l₁ǁ l₂:A₁:A₂=B₁:B₂ ,k₁=k₂ , 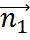ǁ 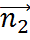, l_{1 ┴} l₂:

A₁A₂+B₁B₂=0, k₁= - ,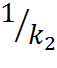

(

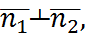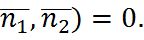
Плоскость в пространстве.

1.Общее уравнение плоскости:Ax+By+Cz+D=0 ( ).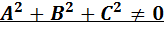

Вектор перпендикулярный данной плоскостиназ.нормальным вектором этой плоскости. В частности, вектор 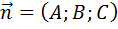-нормальный вектор данной плоскости.

Частные случаи:а) если D=0, то Ax+By+Cz=0. Она проходит через начало координат;б)если А=0, то By+Cz+D=0, плоскость параллельна оси Ox;в)при В=0, то Ax+Cz+D=0параллельна Оy;г)при С=0, то п+By+D=0 параллельна оси Оz;е)если А=0, В=0 то Сz+D=0 параллельна плоскостиOxy, если А=0, С=0 то By+D=0 параллельна плоскостиOxz, если В=0 и С=0, то Ax+D=0 параллельна плоскостиОуz.

2.Уравнение плоскости, проход-ей через точку 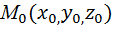перпенд-ую вектору n=(A,B,C) -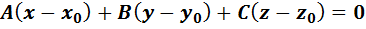

3.Уравнение плоскости в нормальном виде: 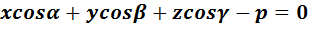,где α,β,γ – углы между осямиOx,Oy,Oz и перпендикуляром, опущенным из начала координат на плоскость,р– длина этого перпендикуляра.

4.Уравнение плоскости в отрезках на оси: 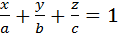, где a,b,c–величины отрезков,отсекаемых плоскостью на координатных осях.

5.Уравнение плоскости по трем точкам 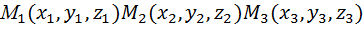: 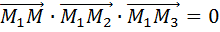(M(x,y,z) – произвольная точка плоскости)или в координатной форме :

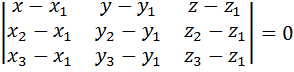
Прямая в пространстве.

1)Каноническое уравнениепрямой, проходящей через точку 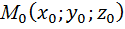паралельно вектору 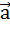=(m;n;p):

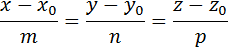
2)Параметрические уравнения прямой:

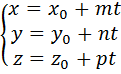где t–переменный параметр.

3)две точки M₁(x₁, y₁, z₁) и M₂(x_2, y₂, z₂), тогда уравнение прямой, проходящей через эти точки:

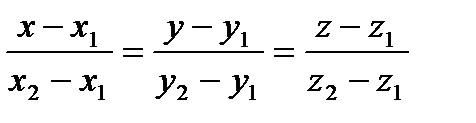
4)Общее уравнениепрямой:

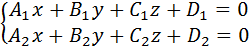
Направляющий вектор прямой находится по формуле:

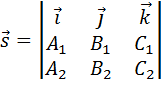, или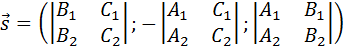

Взаимное расположение двух прямых:

l2: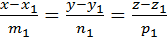

l1: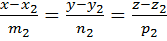

(^.)M₁(x₁;y₁;z₁), (^.)M₂(x₂;y₂;z₂)

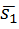(m₁;n₁;p₁) 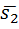(m₂;n₂;p₂) <φ

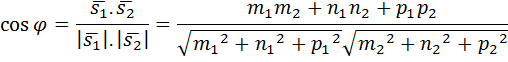
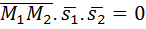
Цилиндрические поверхности.

Поверхности второго порядка– это поверхности, уравнения которых в прямоугольной системе координат являются уравнениями второго порядка.

1)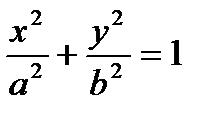 - эллиптический цилиндр.

2) 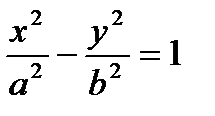- гиперболический цилиндр.

3) x² = 2py – параболический цилиндр.

Производная

Пусть функция у=f(x) определена в некоторой окрестности точки х0, если переменная х получит приращение ∆х, то переменная у получит приращение ∆у=∆у(х0)= ∆f(х0)=f(х0+∆х)-f(х0)

Опр.1 Производной функции у=f(x) в т. х0 называется =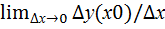

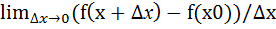
Производная функции f(x) в т. х обознач. у’=у’(x)=f’(x)= df/dx=dy/dx

При каждом конкретном значении х производная (если она сущ.) представляет собой некоторое число, таким образом конечному знач. х ставится в соотв. f’(x). Полученая функция как бы произведена от f(x). Этим объясняется понятие производной.

Операция нахождения производной назыв. дифференцированием.

Пусть кривая l является гр. функц. у=f(x) и точка М0(х0;f(x0))принадл. L. Рассмотрим некоторую секущую М0М

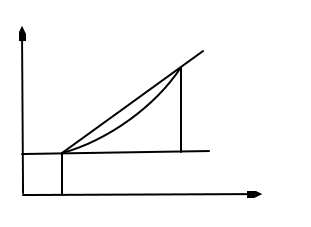
Угловой коэффициент секущей tgɸ=∆y/∆x, если т. М движ. По кривой в т. М0, то сек. М0М стемится к некоторому предельному положению наз.касательной, угловой коэф. Которой К= 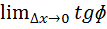= =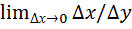y’(x0).

Таким образом геометрич. смысл произв. следующий: производная ф. в т. х0 ровна угл. Коэф. Косательной и гр. функции у=f(x) в т. х0: y-f(x0)=f’(x0)(x-x0)

Cмеханич. Точки зрения произв. ф. представляет собой мгновенную скорость процесса. Например произв. пути по времени- скорость, произвскороти- ускорение.

Опр 2: Функция y=f(x) назыв. дифференцируемой в т. х0, если она имеет в т х0 конечную произв.

Функция назыв. Дифференцируемой, если она дифф. В каждой точке интервала.

Т1: Если функция f(x) диффер в т. х0 то она в этой точке непрерывна.

Док-во: 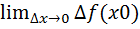= = 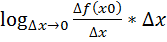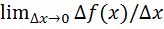* 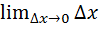=f’(x0)*0

Замечание: Утверждение обратное т1 не имеет места. Например у= 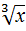непрерывна в т. х=0, но не фифференцируема или ф. у= 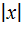непрерывна в т. х=0, но не дифф. В ней.

Дифференциал функции

Под дифференциалом функцииdy функцииy=f(x) понимается главная часть её приращения ∆у, пропорциональная приращению ∆х независимой х.

Дифференциалdx независимой переменной х равен её приращению dx=∆x.

Дифференциал любой дифференцируемой функцииy=f(x) равен произведению её производной на дифференциал независимой переменной dy=f’(x)dx

Из формулы dy=f’(x)dxвытекает представление производ. в виде частного двух дифференциаловf‘(x)=dy/dx

Если ∆х достаточно мало по модулю, то с точностью до бесконечно малых более высокого порядка малости, чем ∆х, имеет место приближённое равенство ∆у≈dy или

f(x+∆x)≈f(x)+f’(x)*∆x

Соотношение f(x+∆x)≈f(x)+f’(x)*∆xиспользуют в приближённых вычислениях.

Правило Лопиталя.

Если функции f(x) и g(x) дифференцируемы в вблизи точки а, непрерывны в точке а, g¢(x) отлична от нуля вблизи а и f(a) = g(a) = 0, то предел отношения функций при х®а равен пределу отношения их производных, если этот предел (конечный или бесконечный) существует.

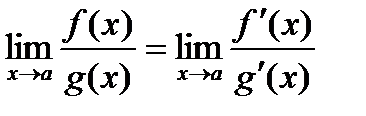
Доказательство. Применив формулу Коши, получим:

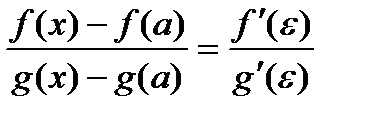
где e - точка, находящаяся между а и х. Учитывая, что f(a) = g(a) = 0:

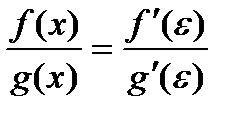
Пусть при х®а отношение 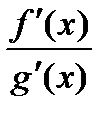стремится к некоторому пределу. Т.к. точка e лежит между точками а и х, то при х®а получим e®а, а следовательно и отношение 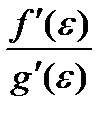стремится к тому же пределу. Таким образом, можно записать:

.

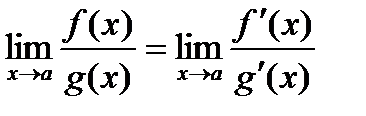Теорема доказана.

Неопределенности вида 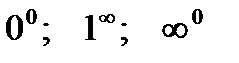можно раскрыть с помощью логарифмирования. Такие неопределенности встречаются при нахождении пределов функций вида 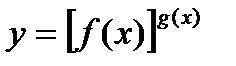, f(x)>0 вблизи точки а при х®а. Для нахождения предела такой функции достаточно найти предел функции lny = g(x)lnf(x).

Асимптоты

Асимптотой кривой называется прямая , к которой неограниченно приближается точка кривой при неограниченном удалении её от начала координат.

Различают вертикальные и наклонные асимптоты.

Прямая X=a является вертикальной асимптотой графики функции y=f(x) , если , по крайней мере , один из односторонних пределов в точке .x=a равен бесконечности т.е.

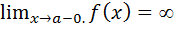или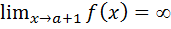

Прямаяy=k1x+b1 является наклонной асимптотой при x->+∞ если существуют оба предела

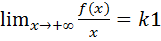и b1=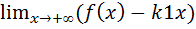

Аналогично, если существуют пределы

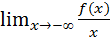K1= и b1=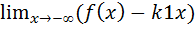

То прямаяy=k2x+b2 является наклонной асимптотой приx->-∞

Если k=0 и существует 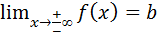, то получаем горизонтальную асимптоту y=bкак частный случай наклонной.

Если вертикальных асимптот может быть любое число , то наклонных асимптот не может быть более 2-ух.

Частные производные.

Определение. Пусть в некоторой области задана функция z = f(x, y). Возьмем произвольную точку М(х, у) и зададим приращение Dх к переменной х. Тогда величина D_xz = f( x + Dx, y) – f(x, y) называется частным приращением функции по х.

Можно записать

.

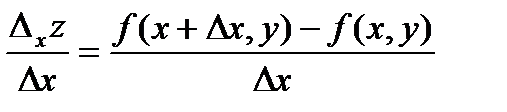
Тогда 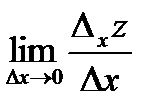называется частной производной функции z = f(x, y) по х.

Обозначение: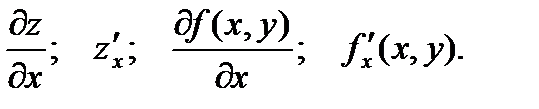

Аналогично определяется частная производная функции по у.

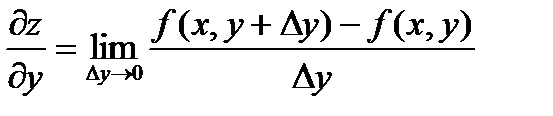
Геометрическим смыслом частной производной (допустим 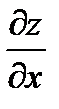) является тангенс угла наклона касательной, проведенной в точке N0(x0, y0, z0) к сечению поверхности плоскостью у = у0.

Опредетели n-ого порядка.

Определители n-го порядка.

4.Обратная матрица.Критерии её сущ-ния.
Обратная матрица.

5.Ранг матрицы.Элементарные преобразования матриц.Нахождения ранга с их помощью
Ранг матрицы.

Теорема Крамера.

Прямая на плоскости.

Плоскость в пространстве.

Прямая в пространстве.

Комплексные числа.

Производная

Дифференциал функции

Правило Лопиталя.

Асимптоты

Частные производные.

Матрицы. Сложение матриц и умножение на число.Их свойства.

Пусть m,n- целые положительные числа и M- непустое множество элементов любой природы. Матрицейразмеров m*n над М или m*n –матрицей над M называется прям.таблица,составленная из mnэлементов множества М и содержащаяm строк и n столбцов.

Пусть A=(а_i,j)_m*n и B=(b_i,j)_m*n две матрицы одинаковой размерности,сумма матриц A и B, называется матрица такой же размерности, у которой каждый элемент равен сумме элементов A и B.

Произведение матрицы A=(а_i,j)_m*n на число С( С? R),называется m*n – матрица такой же размерности, у которой каждый элемент равен произведению соотв. элемента матрицы A на число С.

1. A+B=B+A(коммунативность сложения)

2. (A+B)+C=A+(B+C)(ассоциативность)

3. A+0=A

4. A+(-A)=0

5. α(A+B)=αA+αB

6. (α+β)A=αA+βB

7. (αβ)A=α(βA)

8. 1*A=A