Свойства суммы матриц и произведения матрицы на число.

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ

_

Кафедра высшей математики

ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ПРАКТИЧЕСКИМ ЗАНЯТИЯМ И

ВЫПОЛНЕНИЮ РАСЧЕТНОГО ЗАДАНИЯ

ДЛЯ СТУДЕНТОВ ЗАОЧНОГО ОТДЕЛЕНИЯ

Москва 2007

С о с т а в и т е л и:

доцент, кандидат физико-математических наук Е.Е.Ассеева,

доцент Т.А.Мацеевич,

доцент, кандидат физико-математических наук И.Б.Раскина,

ассистент А.Н.Федосова.

ГЛАВА 1. МАТРИЦЫ.

Основные понятия.

Определение 1. Матрицей размерности 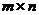(читается 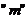на ) на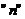зывается прямоугольная таблица чисел, состоящая из 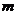строк и 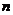столбцов:

.

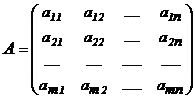Числа 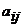называются элементами матрицы 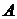, индекс 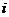указывает номер строки, индекс 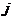- номер столбца, на пересечении которых находится элемент 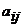. Так, например, элемент 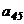стоит на пересечении четвертой строки и пятого столбца.

Для обозначения матрицы используются следующие символы:

, , , , ,

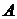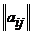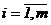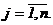
Определение 2. Матрица 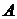называется квадратной матрицей 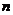- ого порядка, если 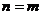(число строк равно числу столбцов):

.

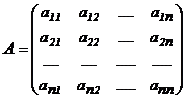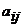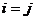Элементы , где , называются диагональными элементами матрицы .

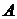Определение 3. Квадратная матрица 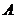называется диагональной, если 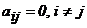(все элементы матрицы, за исключением, быть может, диагональных, равны нулю):

.

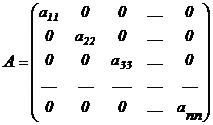Определение 4. Диагональная матрица 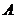называется единичной, если все ее диагональные элементы равны единице ( 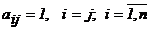). Единичная матрица обычно обозначается буквой :

.

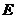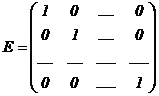Для обозначения единичной матрицы используют также символ Кронекера:

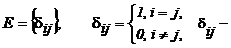символ Кронекера.

Определение 5. Матрица называется нулевой, если все ее элементы равны нулю:

.

Матрицей – столбцом называется матрица 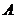, состоящая из одного столбца (размерность ):

.

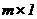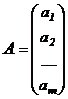Матрицей – строкой называется матрица 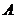, состоящая из одной строки (размерность ):

.

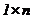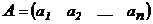Определение 6. Две матрицы 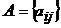и 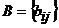называются равными, если

1) размерности матриц совпадают;

2) соответствующие элементы матриц равны:

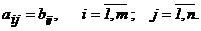
Пусть задана матрица 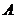размерности 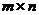. Заменим 1-ую строку на 1-ый столбец, 2-ую строку на 2-ой столбец и т.д., 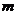-ую строку на 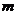-ый столбец. Такая операция называется транспонированием матрицы .

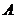Определение 7. Матрица, полученная в результате транспонирования, называется транспонированной по отношению к матрице 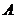и обозначается символом .

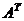Пример. Транспонировать матрицу

,

.

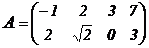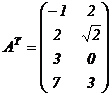§ 2. Определители второго и третьего порядков.

Рассмотрим матрицу 2-го порядка:

.

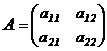Этой матрице соответствует число, которое называется определителем (детерминантом) матрицы .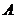

Для обозначения определителя используют символы:

, .

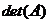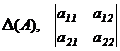Определение 1. Определителем 2-го порядка матрицы 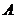называется число:

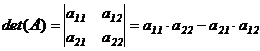. (1)

Например,

.

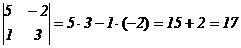Введем понятие определителя 3-го порядка. Пусть

.

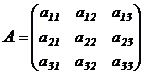Определение 2. Минором элемента 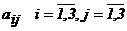матрицы 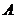называется определитель, который получается из матрицы 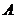вычеркиванием 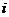-ой строки и 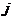-ого столбца. Минор элемента 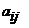обозначается символом .

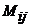Например, для элемента 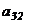матрицы 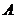минором служит определитель

.

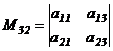Определение 3. Алгебраическим дополнением 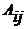элемента 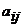матрицы 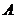называется его минор, умноженный на :

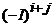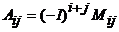. (2)

В качестве примера вычислим алгебраическое дополнение элемента 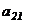матрицы

.

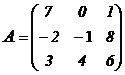В нашем случае 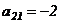, вычеркивая 2-ую строку и 1-ый столбец, получим

, .

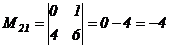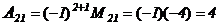Определение 4. Определителем 3-го порядка матрицы 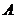называется число

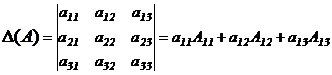. (3)

Поясним это определение на примере:

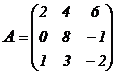, тогда

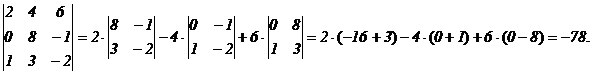
Для вычисления определителя 3-го порядка можно использовать, так называемое, «правило треугольника», а именно:

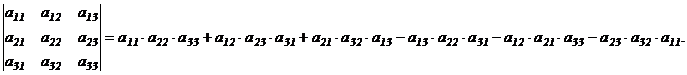
Например,

.

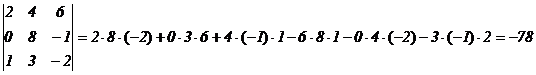§ 3. Определители n-ого порядка.

Введем теперь понятие определителя 4-ого порядка. Аналогично определениям минора и алгебраического дополнения элементов матрицы 3-го порядка, можно ввести эти понятия для элементов матрицы 4-го порядка :

,

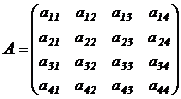понимая под минором 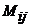( 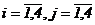) ее элемента 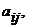определитель матрицы 3-го порядка, которая получается вычеркиванием из матрицы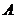 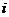–ой строки и 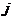–ого столбца, а под алгебраическим дополнением 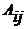– произведение

.

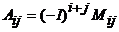Определение 1. Определителем 4-ого порядка называется число

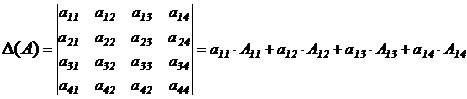. (1)

Аналогичным образом можно ввести понятие определителя 5-ого порядка, опираясь на определение определителя 4-ого порядка.

В общем случае, предположим, что мы определили, что такое определитель

( n- 1)-ого порядка, тогда можно ввести понятиеопределителя n-ого порядка.

Определение 2. Определитель n-ого порядка квадратной матрицы 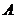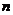-ого порядка

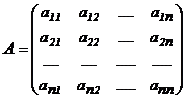
есть число

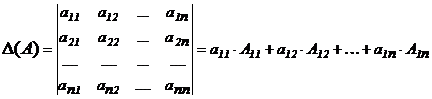, (2)

где 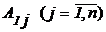- алгебраическое дополнение элемента 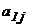матрицы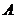

,

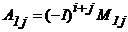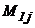- минор элемента 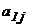матрицы 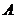, т.е. определитель матрицы 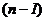-ого порядка, которая получается вычеркиванием из матрицы 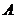1–ой строки и 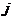–ого столбца.

Формула (2) называется разложением определителя 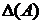по элементам 1-ой строки.

В качестве примера вычислим определитель 4-ого порядка, опираясь на его определение.

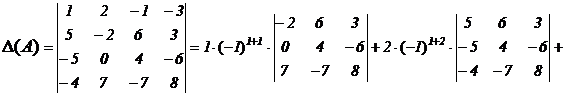
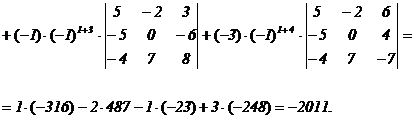
Свойства определителей.

1. При транспонировании квадратной матрицы величина ее определителя не меняется:

.

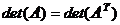2. Если поменять местами две строки (или два столбца), то определитель изменит знак на противоположный.

3. Определитель с двумя одинаковыми строками (столбцами) равен 0.

4. Определитель, содержащий нулевую строку (столбец), т.е. строку (столбец) состоящую только из нулей, равен нулю.

5. Общий множитель всех элементов строки (столбца) можно выносить за знак определителя, например,

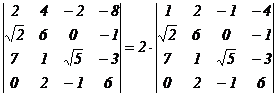
(за знак определителя мы вынесли «2» - общий множитель элементов 1-ой строки).

6. Определитель с двумя пропорциональными строками (столбцами) равен нулю.

7. Если каждый элемент 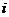–ой строки ( 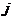–ого столбца) определителя 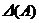представлен в виде суммы двух слагаемых, то

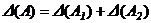, где

в определителях 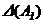и 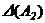все строки (столбцы), кроме 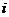–ой строки ( 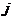–ого столбца) такие же, как и в определителе 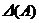; 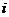–ая строка ( 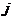–ый столбец) в определителе 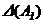состоит из первых слагаемых 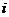–ой строки ( 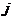–ого столбца) определителя 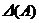, а в определителе 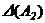- из вторых слагаемых этой строки (столбца).

Поясним сказанное на примере.

.

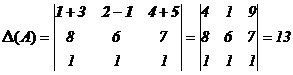В силу свойства 7

.

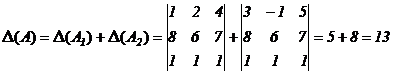8. Величина определителя не изменится, если ко всем элементам некоторой строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и тоже число.

Например,

.

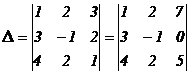Каждый элемент 2-го столбца мы умножили на «2» и прибавили к соответствующему элементу 3- его столбца. Предлагаем читателю вычислить каждый из определителей и убедиться в их равенстве.

9. Определитель равен сумме произведений элементов любой строки (столбца) на соответствующие алгебраические дополнения.

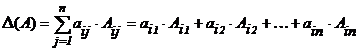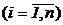, (1)

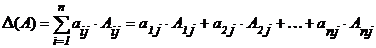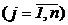, (2)

Равенство (1) называется разложением определителя 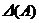по элементам 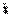–ой строки, а равенство (2) - разложением по элементам 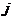-ого столбца.

10. Сумма произведений элементов строки (столбца) на алгебраические дополнения (см. определение 3 §2) элементовдругой строки (столбца) равна нулю.

Опираясь на свойства 8 и 9 можно преобразовать заданный определитель так, чтобы все элементы какой-либо строки (столбца), кроме, быть может, одного, равнялись нулю, а затем разложить определитель по элементам этой строки (столбца), что значительно облегчит вычисления.

Пример. Преобразуем определитель

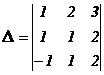
так, чтобы в первой строке все элементы, кроме, быть может, одного, стали нулями. Мысленно умножим элементы первого столбца определителя на «–3» ( 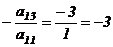) и прибавим результат к соответствующим элементам третьего столбца, получим определитель

.

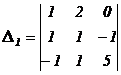Теперь умножим все элементы 1-го столбца определителя 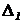на «–2» ( 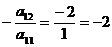) и прибавим результат к соответствующим элементам второго столбца:

.

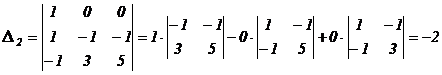В силу свойства 8

.

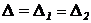Алгебра матриц.

Определение 1. Суммой матриц 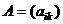и 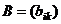одинаковой размерности 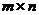называется матрица 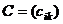размерности 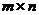, каждый элемент которой равен сумме соответствующих элементов матриц и :

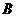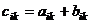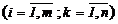, . (1)

Пример 1.

.

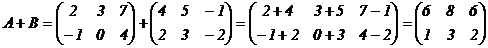Определение 2. Произведением матрицы 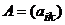на число 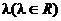называется матрица 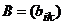размерности 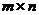, для которой ( ).

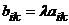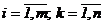Пример 2.

.

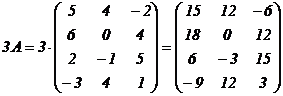Свойства умножения матриц.

1. Ассоциативность

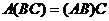, где , , 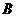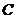- матрицы размерности соответственно: , , .

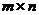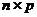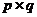2. Дистрибутивность

,

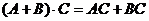
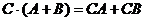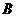где и - матрицы размерности 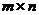, 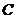- матрица размерности .

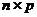3. ,

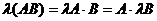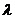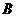где - число, и - матрицы размерности соответственно 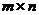и .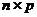

Замечание 3. Произведение матриц в общем случае некоммутативно, т.е. 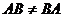, если в частности 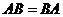, то матрицы и 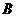называются перестановочными.

Обратная матрица.

Определение 1. Квадратная матрица называется невырожденной, если 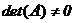и вырожденной, если .

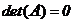Пусть задана квадратная матрица:

.

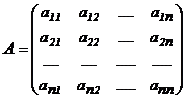Определение 2. Матрица 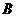называется обратной к матрице , если выполняется равенство 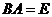, где 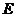- единичная матрица. Матрица, обратная к матрице , обозначается символом :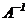

.

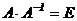Справедлива следующая теорема .

Всякая невырожденная матрица имеет единственную обратную матрицу.

Пусть задана матрица

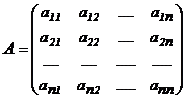
и 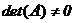, тогда матрицу 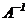можно получить следующим образом:

1) вычисляем определитель матрицы ;

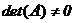2) находим матрицу

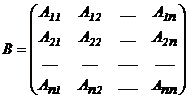
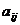(заменим в матрице каждый элемент соответствующим ему алгебраическим дополнением );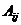

3) транспонируем матрицу 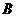, полученная матрица 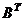называется союзной и обозначается символом :

;

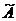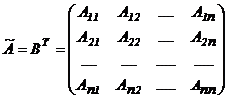4) находим матрицу

.

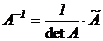Поясним сказанное на примере:

.

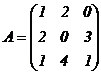1) ;

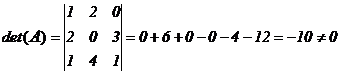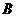2) вычисляем алгебраические дополнения элементов матрицы и находим матрицы и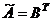

, , ,

, , ,

, , ,

, ;

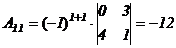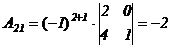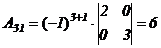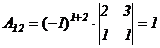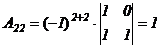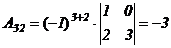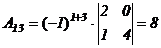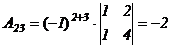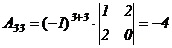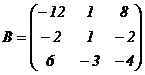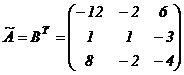4) ;

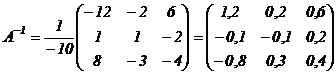5) проверяем:

.

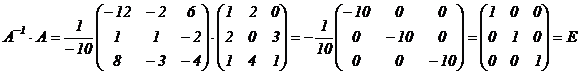Легко убедиться, что

.

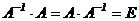Ранг матрицы.

Определение 1. Элементарными преобразованиями матрицы называются следующие действия:

1) вычеркивание нулевых строк (столбцов);

2) перестановка двух строк (столбцов);

3) прибавление к одной из строк (столбцу) другой строки (столбца), умноженной на любое число .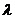

Определение 2. Матрица называется ступенчатой, если ее диагональные элементы 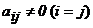, а все элементы, лежащие ниже диагональных, равны нулю ( 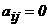, если ).

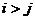Например, матрица

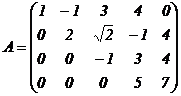- ступенчатая.

Теорема 1. Любую матрицу с помощью элементарных преобразований можно привести к ступенчатому виду.

Теорема 2. При любом способе приведения матрицы с помощью элементарных преобразований к ступенчатому виду количество строк в полученной ступенчатой матрице будет одним и тем же.

Определение 3. Рангом матрицы называется число строк в ступенчатой матрице, которая получается из матрицы элементарными преобразованиями. Ранг матрицы обозначается символами :

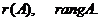
Для вычисления ранга матрицы можно применить следующий алгоритм.

1. Вычеркиваем в матрице все нулевые строки, если они есть.

2. Т.к. теперь нулевых строк нет, то в 1-ой строке полученной матрицы найдется хотя бы один отличный от нуля элемент. Переставим столбцы так, чтобы в 1-ой строке на 1-ом месте стоял элемент, отличный от нуля .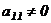

3. Первую строку, умноженную последовательно на 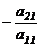; ; 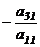; 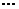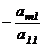, прибавим соответственно ко 2-ой, 3-ей, … , m-ой строке. Получим матрицу :

.

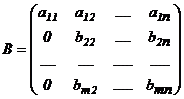Вычеркнем в матрице 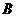нулевые строки, если они есть. Можно считать, что во 2-ой строке есть хотя бы один элемент, отличный от нуля. Переставим столбцы так, чтобы .

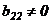4.Умножим 2-ую строку последовательно на 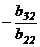; ; 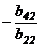; 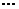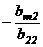и прибавим соответственно к каждой из последующих строк. В результате получим матрицу

.

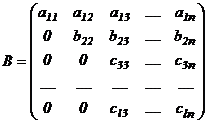Вообще говоря, 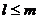, т.к. при переходе от одной матрице к другой некоторые строки (нулевые) могли быть вычеркнуты.

Повторяя описанные рассуждения через конечное число шагов, мы получим матрицу ступенчатого вида, число строк в которой и будет рангом матрицы . Поясним сказанное на примере.

Вычислим ранг матрицы:

.

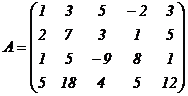Умножим первую строку на «-2» и сложим ее со 2-ой, затем умножим 1-ую строку на «-1» и сложим ее с 3-ей; наконец, первую строку, умноженную на «-5», сложим с 4-ой. Приходим к матрице:

.

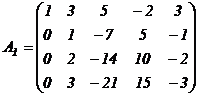В матрице 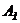вторую строку, умноженную последовательно на «-2» и «-3», складываем соответственно с 3-ей и 4-ой строками, получаем:

.

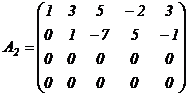Вычеркиваем в матрице 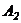третью и четвертую нулевые строки, получим

,

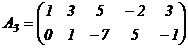число строк в ступенчатой матрице 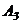равно 2. Следовательно,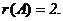

Теорема 3. Ранг матрицы не меняется при транспонировании.

Рекомендуем читателю транспонировать матрицу в рассмотренном примере и убедиться, что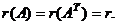

Основные понятия.

Определение 1. Системой m линейных уравнений с n неизвестными называется система вида:

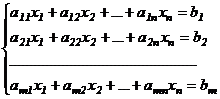, (I)

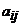где и 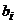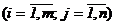- числа.

Определение 2. Решением системы (I) называется такой набор неизвестных 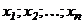, при котором каждое уравнение этой системы обращается в тождество.

Определение 3. Система (I) называется совместной, если она имеет хотя бы одно решение и несовместной, если она не имеет решений. Совместная система называется определенной, если она имеет единственное решение, и неопределенной в противном случае.

Определение 4. Уравнение вида

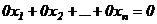
называется нулевым, а уравнение вида

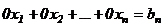, где

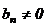
называется несовместным. Очевидно, что система уравнений, содержащая несовместное уравнение, является несовместной.

Определение 5. Две системы линейных уравнений называются равносильными, если каждое решение одной системы служит решением другой и, наоборот, всякое решение второй системы является решением первой.

Метод Гаусса.

Пусть задана система линейных уравнений:

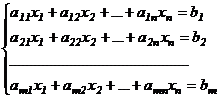. (I)

Требуется найти все решения системы (I) или убедиться в том, что система несовместна.

Определение 1. Назовем элементарным преобразованием системы (I) любое из трёх действий :

1) вычёркивание нулевого уравнения;

2) прибавление к обеим частям уравнения соответствующих частей другого уравнения, умноженных на число l;

3) перемена местами слагаемых в уравнениях системы так, чтобы неизвестные с одинаковыми номерами во всех уравнениях занимали одинаковые места, т.е. если, например, в 1-ом уравнении мы поменяли 2-ое и 3-е слагаемые, тогда то же самое необходимо сделать во всех уравнениях системы.

Метод Гаусса состоит в том, что система (I) с помощью элементарных преобразований приводится к равносильной системе, решение которой находится непосредственно или устанавливается её неразрешимость.

Как было описано в §2 система (I) однозначно определяется своей расширенной матрицей и любое элементарное преобразование системы (I) соответствует элементарному преобразованию расширенной матрицы :

.

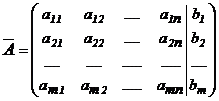Преобразование 1) соответствует вычёркиванию нулевой строки в матрице 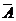, преобразование 2) равносильно прибавлению к соответствующей строке матрицы 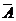другой её строки, умноженной на число l, преобразование 3) эквивалентно перестановке столбцов в матрице .

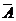Легко видеть, что, наоборот, каждому элементарному преобразованию матрицы 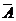соответствует элементарное преобразование системы (I). В силу сказанного, вместо операций с системой (I) мы будем работать с расширенной матрицей этой системы.

В матрице 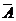1-ый столбец состоит из коэффициентов при х₁, 2-ой столбец - из коэффициентов при х₂ и т.д. В случае перестановки столбцов следует учитывать, что это условие нарушается. Например, если мы поменяем 1-ый и 2-ой столбцы местами, то теперь в 1-ом столбце будут коэффициенты при х₂, а во 2-ом столбце - коэффициенты при х₁.

Будем решать систему (I) методом Гаусса.

1. Вычеркнем в матрице 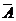все нулевые строки, если такие имеются (т.е. вычеркнем в системе (I) все нулевые уравнения).

2. Проверим, есть ли среди строк матрицы 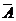строка, в которой все элементы, кроме последнего, равны нулю (назовём такую строку несовместной). Очевидно, что такой строке соответствует несовместное уравнение в системе (I) , следовательно, система (I) решений не имеет и на этом процесс заканчивается.

3. Пусть матрица 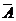не содержит несовместных строк (система (I) не содержит несовместных уравнений). Если a₁₁=0, то находим в 1-ой строке какой-нибудь элемент (кроме последнего) отличный от нуля и переставляем столбцы так, чтобы в 1-ой строке на 1-ом месте не было нуля. Будем теперь считать, что 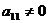(т.е. поменяем местами соответствующие слагаемые в уравнениях системы (I)).

4. Умножим 1-ую строку на 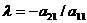и сложим результат со 2-ой строкой, затем умножим 1-ую строку на 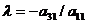и сложим результат с 3-ей строкой и т.д. Очевидно, что этот процесс эквивалентен исключению неизвестного x₁ из всех уравнений системы (I), кроме 1-ого. В новой матрице 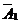получаем нули в 1-ом столбце под элементом a₁₁ :

.

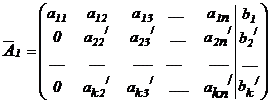5. Вычеркнем в матрице 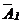все нулевые строки, если они есть, проверим, нет ли несовместной строки (если она имеется, то система несовместна и на этом решение заканчивается). Проверим, будет ли a₂₂ ^/=0, если да, то находим во 2-ой строке элемент, отличный от нуля и переставляем столбцы так, чтобы 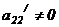. Далее умножаем элементы 2-ой строки на 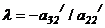и складываем с соответствующими элементами 3-ей строки, затем - элементы 2-ой строки на 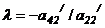и складываем с соответствующими элементами 4-ой строки и т.д., пока не получим нули под a₂₂ ^/

.

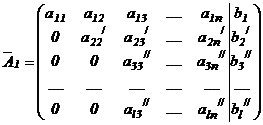Произведенные действия эквивалентны исключению неизвестного х₂ из всех уравнений системы (I), кроме 1-ого и 2-ого. Так как число строк конечно, поэтому через конечное число шагов мы получим, что либо система несовместна, либо мы придём к ступенчатой матрице (см. определение 2 §7 главы 1) :

,

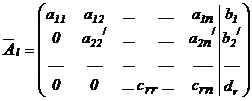где

.

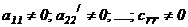Выпишем систему уравнений, соответствующую матрице 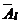. Эта система равносильна системе (I)

.

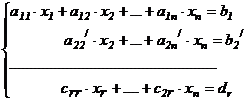Из последнего уравнения выражаем 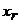; подставляем 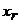в предыдущее уравнение, находим 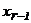и т.д., пока не получим .

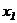Замечание 1. Таким образом, при решении системы (I) методом Гаусса мы приходим к одному из следующих случаев.

1. Система (I) несовместна.

2. Система (I) имеет единственное решение, если в матрице 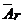число строк равно числу неизвестных ( ).

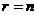3. Система (I) имеет бесчисленное множество решений, если число строк в матрице 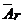меньше числа неизвестных ( ).

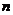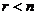Отсюда имеет место следующая теорема.

Теорема. Система линейных уравнений либо несовместна, либо имеет единственное решение, либо – бесконечное множество решений.

Примеры. Решить систему уравнений методом Гаусса или доказать ее несовместность:

а) ;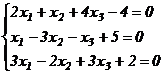

б) ;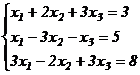

в) .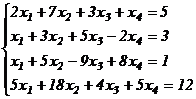

Решение.

а) Перепишем заданную систему в виде:

.

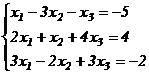Мы поменяли местами 1-ое и 2-ое уравнение исходной системы, чтобы упростить вычисления (вместо дробей мы с помощью такой перестановки будем оперировать только целыми числами).

Составляем расширенную матрицу:

.

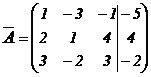Нулевых строк нет; несовместных строк нет, 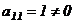; исключим 1-ое неизвестное 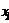из всех уравнений системы, кроме 1-го. Для этого умножим элементы 1-ой строки матрицы 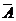на «-2» и сложим с соответствующими элементами 2-ой строки, что равносильно умножению 1-го уравнения на «-2» и сложению со 2-ым уравнением. Затем умножим элементы 1-ой строки на «-3» и сложим с соответствующими элементами третьей строки, т.е. умножим 2-ое уравнение заданной системы на «-3» и сложим с 3-им уравнением. Получим

.

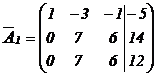Матрице 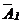соответствует система уравнений

.

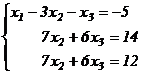В матрице 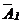нулевых строк нет, несовместных строк также нет, исключим неизвестное 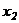из 3-го уравнения системы, для этого умножим элементы 2-ой строки матрицы 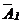на «-1» и сложим с элементами 3-ей строки :

.

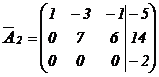Матрица 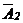содержит несовместную строку (в 3-ей строке все элементы равны нулю, кроме последнего). Этой строке соответствует несовместное уравнение 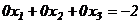. Следовательно, система решений не имеет (