Прямоугольные декартовы координаты вектора.
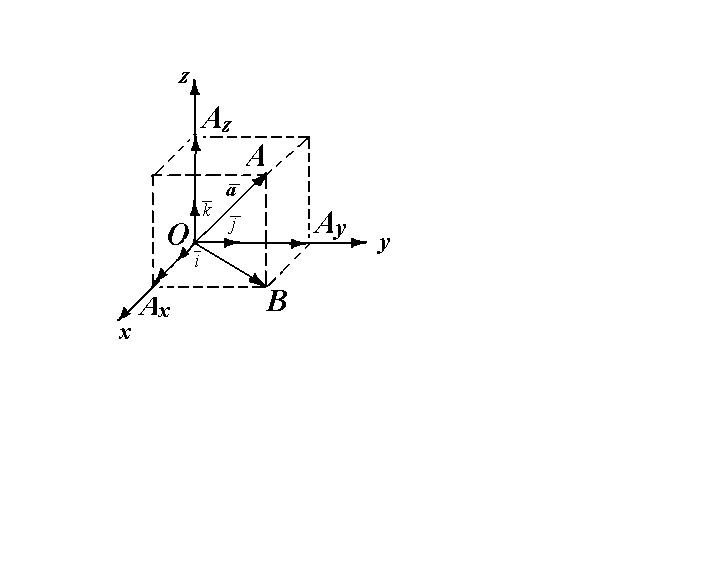
| Рис. 1 |
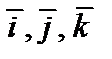 – единичные векторы соответствующих осей координат Ох, Оу, Оz, т.е.
– единичные векторы соответствующих осей координат Ох, Оу, Оz, т.е. 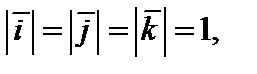 и каждый из них одинаково направлен с соответствующей осью координат (рис. 1). Тройка векторов
и каждый из них одинаково направлен с соответствующей осью координат (рис. 1). Тройка векторов 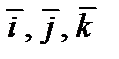 называется базисом.
называется базисом. Теорема 1.Любой вектор 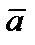 можно единственным образом разложитьпо базису
можно единственным образом разложитьпо базису 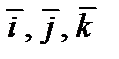 , т.е. представить в виде
, т.е. представить в виде
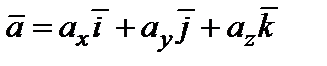 , (1)
, (1)
где 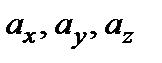 - числа
- числа
22. Определение скалярного произведения, его свойства имеханический смысл.Скалярным произведением 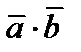 двух ненулевых векторов
двух ненулевых векторов 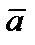 и
и 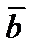 называется число, равное произведению длин векторов на косинус угла между ними. Если хотя бы один из векторов
называется число, равное произведению длин векторов на косинус угла между ними. Если хотя бы один из векторов 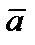 и
и 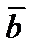 нулевой, то скалярное произведение равно нулю.
нулевой, то скалярное произведение равно нулю.
Таким образом,
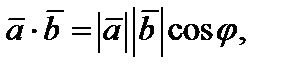 (4)
(4)
где 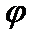 – угол между векторами
– угол между векторами 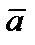 и
и 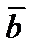 (рис. 2).
(рис. 2).
Скалярное произведение обозначают символом 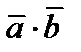 , или
, или 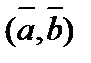 , или
, или 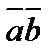 .
.
По формуле 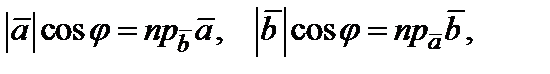 поэтому выражение (4) можно записать:
поэтому выражение (4) можно записать:
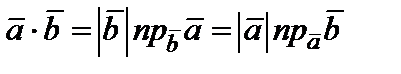 .(5)
.(5)
Для скалярного произведения векторов справедливы следующие свойства:
1) 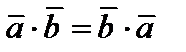 – коммутативность;
– коммутативность;
2) 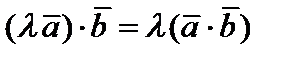 – ассоциативность,
– ассоциативность, 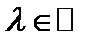 ;
;
3) 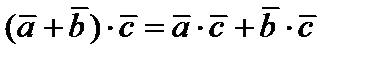 – дистрибутивность;
– дистрибутивность;
4) 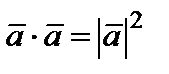 .Доказательство. Коммутативность скалярного произведения непосредственно вытекает из формулы (4).
.Доказательство. Коммутативность скалярного произведения непосредственно вытекает из формулы (4).
Докажем свойство 2). С учетом формул (5) , будем иметь
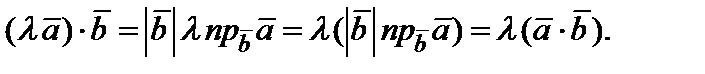 (6)
(6)
Доказательство свойства 3). По формуле (5)
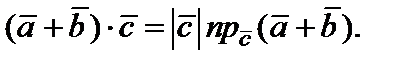 (7)
(7)
Согласно формуле (),
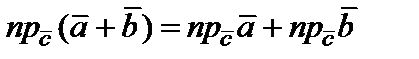 .
.
Таким образом, с учетом (7) и формулы (5), получаем
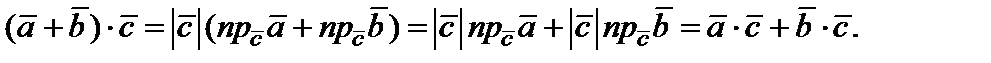
Для доказательства свойства 4) заметим, что по формуле (4) 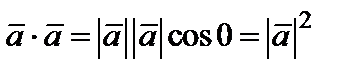 , если
, если 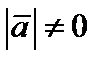 , т.е. если
, т.е. если 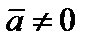 . Если же
. Если же 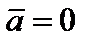 , то также, по определению скалярного произведения,
, то также, по определению скалярного произведения, 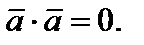 Но, тогда
Но, тогда 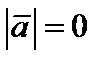 и, поэтому, равенство
и, поэтому, равенство 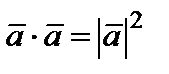 в случае
в случае 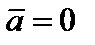 также справедливо. □
также справедливо. □
Скалярное произведение 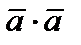 называется скалярным квадратом вектора
называется скалярным квадратом вектора 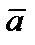 и обозначается
и обозначается 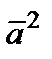 . На основании свойства 4) имеем:
. На основании свойства 4) имеем: 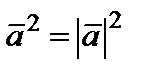 , отсюда, в частности,
, отсюда, в частности, 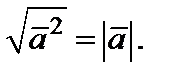
Из свойств 1) и 2) вытекает, что
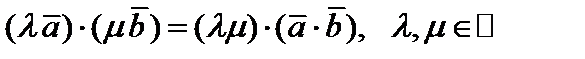 .(8)
.(8)
Из свойства 3) следует, что при скалярном умножении векторных многочленов можно выполнять действия почленно и, в силу (8), объединять коэффициенты векторных сомножителей
23. Перпендикулярности двух векторов. Сформулируем необходимое и достаточное условие перпендикулярности двух векторов.
Свойство5). Два ненулевых вектора 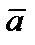 и
и 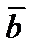 перпендикулярны тогда и только тогда, когда их скалярное произведение
перпендикулярны тогда и только тогда, когда их скалярное произведение 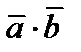 равно нулю.
равно нулю.
Доказательство. Необходимость. Пусть 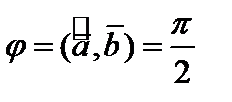 и
и 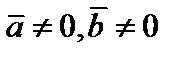 . Тогда
. Тогда 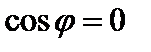
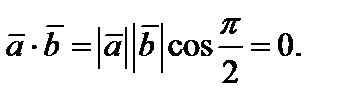
Достаточность. Пусть 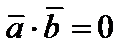 и
и 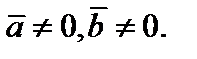 Используя формулу (4), получаем
Используя формулу (4), получаем 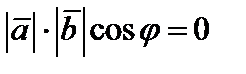 лишь если
лишь если 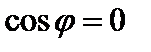 или
или 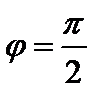 . Значит,
. Значит, 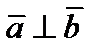 . □
. □
Из равенства (4) получаем формулу для определения косинуса угла между ненулевыми векторами:
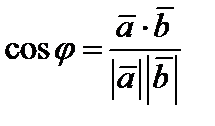 .(9)
.(9)
Отметим, что из свойств 4) и 5) для базисных векторов 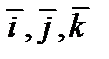 непосредственно получаем следующие равенства:
непосредственно получаем следующие равенства:
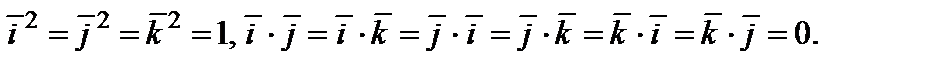
Выражение скалярного произведения через координаты векторов. Если векторы 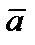 и
и 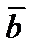 заданы своими координатами:
заданы своими координатами: 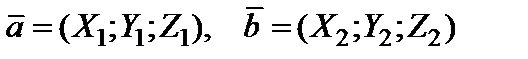 , то их скалярное произведение вычисляется по формуле
, то их скалярное произведение вычисляется по формуле
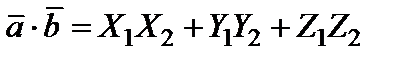 .(11)
.(11)
Доказательство. Разложим векторы 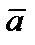 и
и 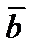 по базису
по базису 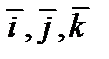 согласно формуле (4):
согласно формуле (4):
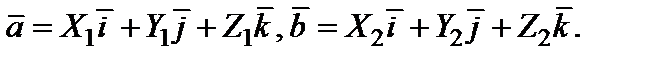
Тогда
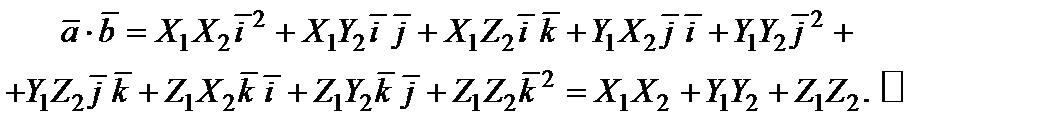 (12)
(12)
Из формулы (8) и свойства 5) вытекает необходимое и достаточное условие перпендикулярности ненулевых векторов 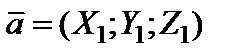 и
и 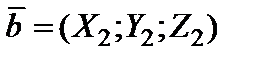 : сумма произведений одноименных координат этих векторов равна нулю, т.е.
: сумма произведений одноименных координат этих векторов равна нулю, т.е.
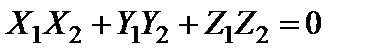 .
.
24. Ориентация тройки векторов в пространстве. Тройку векторов называют упорядоченной, если указано, какой из векторов считается первым, какой вторым и какой третьим. В записи 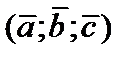 вектор
вектор 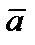 считается первым,
считается первым, 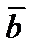 – вторым,
– вторым, 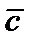 – третьим; в записи
– третьим; в записи 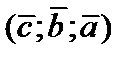 вектор
вектор 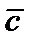 – первый,
– первый, 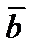 – второй,
– второй, 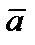 – третий.
– третий.
Упорядоченная тройка некомпланарных векторов называется правой, если после приведения их к общему началу кратчайший поворот от первого ко второму вектору наблюдается с конца третьего вектора против часовой стрелки. В противном случае указанная тройка векторов называется левой.
25. Векторное произведение двух векторов, его свойства, геометрический и физический смысл.Векторным произведениемвекторов 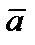 и
и 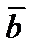 называется вектор
называется вектор 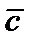 , длина которого численно равна площади параллелограмма, построенного на векторах
, длина которого численно равна площади параллелограмма, построенного на векторах 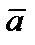 и
и 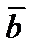 , приведенных к общему началу, который перпендикулярен перемножаемым векторам и направлен так, что векторы
, приведенных к общему началу, который перпендикулярен перемножаемым векторам и направлен так, что векторы 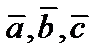 образуют правую тройку векторов (рис. 1).
образуют правую тройку векторов (рис. 1).
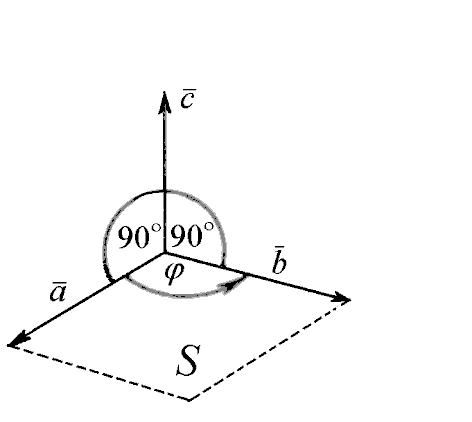 Рис. 1 Рис. 1 | 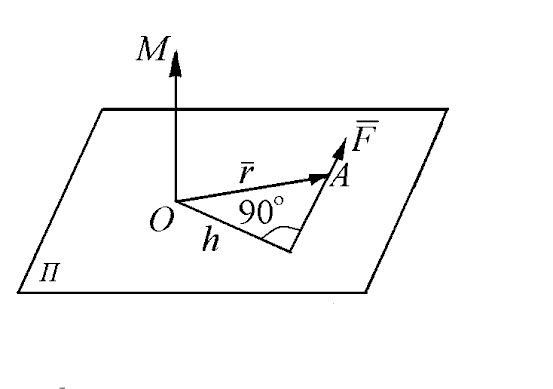 Рис. 2 Рис. 2 |
Если векторы 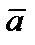 и
и 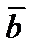 коллинеарны, то их векторное произведение равно нулевому вектору.
коллинеарны, то их векторное произведение равно нулевому вектору.
Из определения векторного произведения следует, что (рис.1)
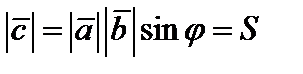 , (1)
, (1)
где 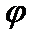 – угол между векторами
– угол между векторами 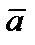 и
и 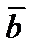 , S – площадь параллелограмма.
, S – площадь параллелограмма.
Векторное произведение двух векторов 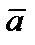 и
и 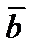 обозначают символом
обозначают символом
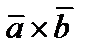 , или
, или 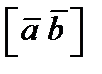 , или
, или 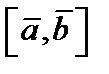 .
.
Выясним физический смысл векторного произведения. В физике момент силы 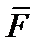 с точкой приложения А относительно точки О изображают вектором
с точкой приложения А относительно точки О изображают вектором 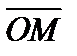 , перпендикулярным плоскости, в которой лежат точка О и вектор
, перпендикулярным плоскости, в которой лежат точка О и вектор 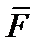 (рис. 2), таким, что тройка векторов
(рис. 2), таким, что тройка векторов 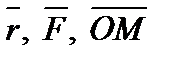 – правая. Длина вектора
– правая. Длина вектора 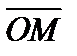 определяется как произведение длины вектора
определяется как произведение длины вектора 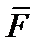 на плечо
на плечо 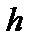 , где
, где 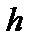 – расстояние от точки О до прямой, на которой лежит вектор силы
– расстояние от точки О до прямой, на которой лежит вектор силы 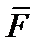 , т.е.
, т.е. 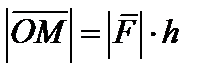 , или
, или 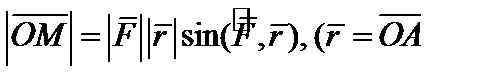 – радиус–вектор точки приложения силы
– радиус–вектор точки приложения силы 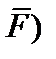 . Таким образом, момент силы
. Таким образом, момент силы 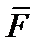 относительно некоторой точки
относительно некоторой точки 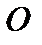 , есть векторное произведение радиус–вектора
, есть векторное произведение радиус–вектора 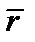 точки приложения силы на вектор силы
точки приложения силы на вектор силы 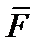 :
: 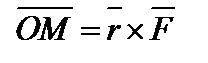 .
.
