Системы ДУ с постоянными коэффициентами

ЛОС ДУ с постоянными коэффициентами.

Эта система имеет вид

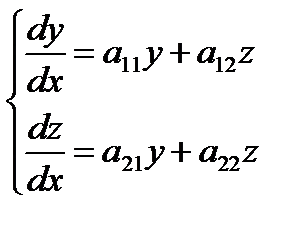(4.1)

где 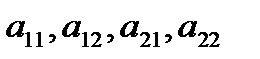- постоянные. Система (4.1) имеет фундаментальную систему решений, состоящую из элементарных функций. Основным методом построения фундаментальной системы решений (4.1) является метод Эйлера. Согласно этому методу, решение ЛОС ДУ ищется в виде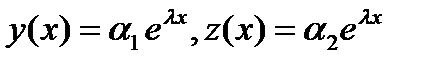

Дифференцируем обе функции по x и подставляем в (4.1):

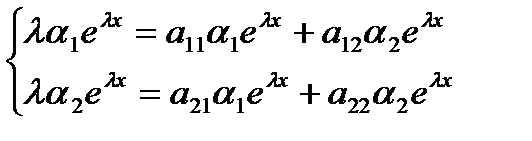
Сокращаем оба уравнения системы на :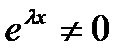

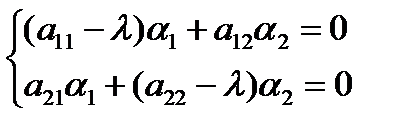(4.2)

Так как 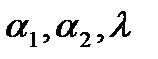- некоторые постоянные числа, подлежащие определению, среди которых хотя бы одно отлично от нуля, то определитель системы (4.2) должен быть равен нулю

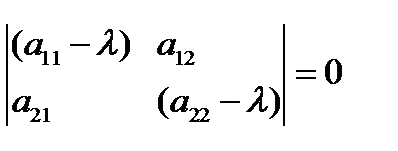(4.3)

Уравнение (4.3) называется характеристическим уравнением, а его корни – характеристическими числами системы (4.1). Каждому из корней характеристического уравнения соответствует хотя бы одно частное решение указанного выше вида. Различают три случая.

Оба корня характеристического уравнения вещественны и различны: 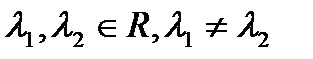. Подставляем 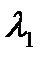в одно из уравнений системы (4.2), например, в первое уравнение: 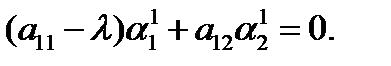Из него с точностью до константы определяем 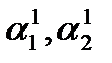, откуда получаем первое решение ЛОС ДУ: 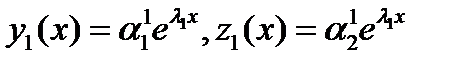. То же самое проделываем со вторым корнем характеристического уравнения 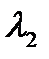и в результате получаем второе, линейно независимое на 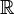, решение ЛОС ДУ: 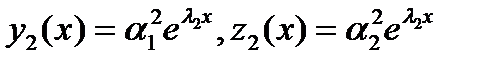. Следовательно, согласно теореме 2 §3 общим решением системы (4.1) будет следующее семейство функций:

.

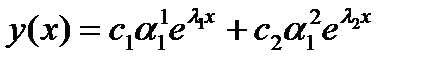
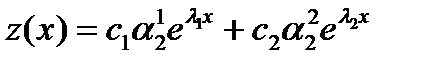2. Если 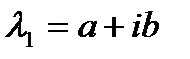- корень характеристического уравнения, то 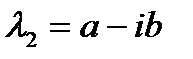. Подставляем 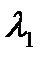в одно из двух уравнений системы (4.2) и с точностью до постоянной получаем 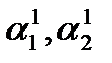. Теперь можно составить первое решение системы (4.1):

.

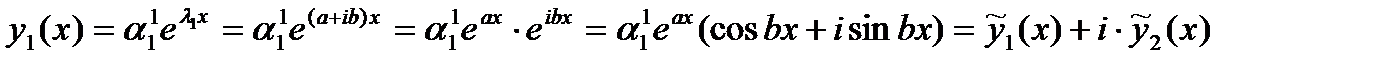
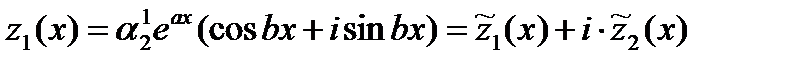Отделив вещественную и мнимую части, получим два вещественных линейно независимых частных решения системы (4.1), соответствующих корню a+ib. Решения, соответствующие корню a-ib, будут линейно зависимы с решениями, соответствующими крню a+ib.

Итак, общее решение ЛОС ДУ в этом случае имеет вид:

.

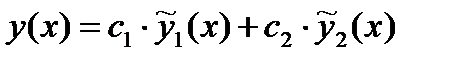
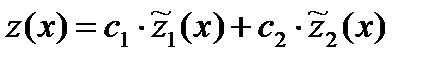3.

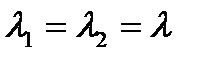
В случае кратного корня характеристического уравнения предлагается представить общее решение системы уравнений (4.1) в следующем ви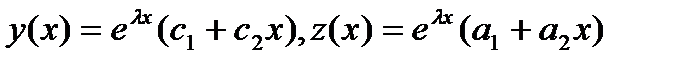де: , где 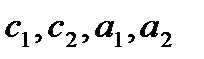- постоянные числа, причем 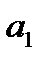и 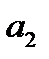должны быть выражены через 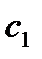и 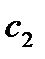. Рассмотрим поясняющий пример.

25.Решени систем ленейных ДУ высших порядков с постоянным коэффициентам

Интегрирование линейных дифференциальных уравнений связано с понятием линейной независимости функций. Функции у1, у2, .... yn называются линейно зависимыми в данном интервале изменения аргумента х, если в этом интервале выполняется тождество C1y1+C2y2+…+Cnyn=0, где C1, C2, ..., Сn - постоянные, из которых хоть одна отлична от нуля. Если же в данном интервале изменения х указанное тождество выполняется только тогда, когда все постоянные С1, С2, ..., Сn равны нулю, то функции у1, у2, ..., yn называются линейно независимыми в данном интервале.

Необходимое условие линейной зависимости функции: если функции у1, у2, ..., уn линейно зависимы в данном интервале изменения аргумента, то определитель Вронского (вронскиан)

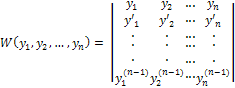
тождественно равен нулю в этом интервале. Отсюда: если W(y1, y2, ..., yn)≠0, то функции линейно независимы в этом интервале (достаточное условие линейной независимости функций).

Пусть дано линейное неоднородное дифференциальное уравнение с постоянными коэффициентами а0, a1, ..., an:

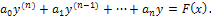
Общее решение имеет вид

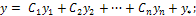
здесь С1, С2, …, Сn - произвольные постоянные; у1, y2, …, yn - линейно независимые решения соответствующего однородного уравнения (система таких решений называется фундаментальной); у* - какое-либо частное решение данного неоднородного уравнения.

Для отыскания у1, у2, ..., уn следует найти корня характеристического уравнения:

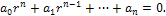
Простому действительному корню rm соответствует решение однородного уравнения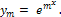

Действительному корню rm кратности k соответствуют решения

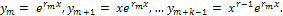
Если rm=α+iβ (комплексный корень), то имеется и сопряженный корень 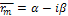; этой паре корней соответствуют

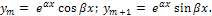
Если rm=α+iβ - комплексный корень кратности k, то имеется и сопряженный корень 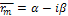той же кратности k; этой паре корней соответствуют решения

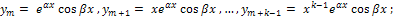
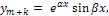
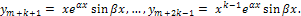
ПРИМЕР 1. Уравнение изгиба балки на упругом основании

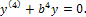
Характеристическое уравнение k4+b4=0 имеет корни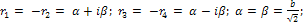

отсюда получаем

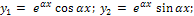
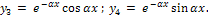
Общее решение однородного уравнения

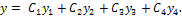
Для нахождения частного решения у* неоднородного уравнения либо применяют способ неопределенных коэффициентов, если правая часть имеет структуру, указанную выше (см. 1.9.4), либо пользуются вариацией произвольных постоянных. При этом в общем случае частное решение у* ищут в форме

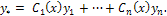
Производные С′i(х) определяют из системы алгебраических линейных уравнений, определитель которой есть определитель Вронского, отличный от нуля в силу линейной независимости решений y1, у2, ..., уn:

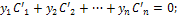
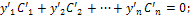
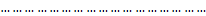
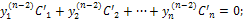
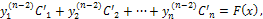
имея C′i(x) находят интегрированием Сi(х).

Наряду с методом вариации произвольных постоянных применяется «символический метод» [1.11.1].