Различные постановки задачи Коши

· ОДУ первого порядка, разрешённое относительно производной

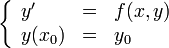
· Система n ОДУ первого порядка, разрешённая относительно производных (нормальная система n-го порядка)

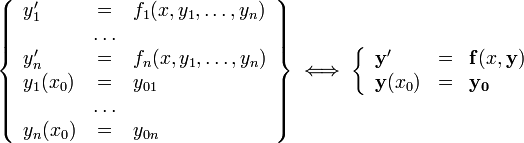
· ОДУ n-го порядка, разрешённое относительно старшей производной

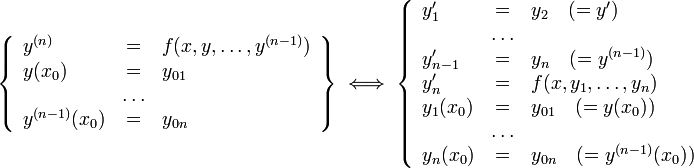
Теоремы о разрешимости задачи Коши для ОДУ

Пусть в области 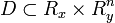рассматривается задача Коши:

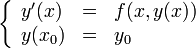
где 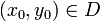. Пусть правая часть является непрерывной функцией в 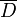. В этих предположениях имеет место теорема Пеано, устанавливающая локальную разрешимость задачи Коши: Пусть a>0 и b>0 таковы, что замкнутый прямоугольник

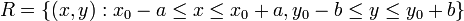
принадлежит области D, тогда на отрезке [x₀ − α,x₀ + α], где α = min{a,b / M}, 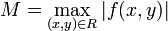, существует решение задачи Коши.

Указанный отрезок называется отрезком Пеано. Заметим, что, локальный характер теоремы Пеано не зависит от гладкости правой части. Например, для f(x,y) = y² + 1 и для x₀ = 0,y₀ = 0 решение y(x) = tan(x) существует лишь на интервале ( − π,π). Также отметим, что без дополнительных предположений относительно гладкости правой части, нельзя гарантировать единственность решения задачи Коши. Например, для 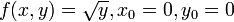возможно более одного решения.

Чтобы сформулировать теорему о единственности решения задачи Коши, необходимо наложить дополнительные ограничения на правую часть. Будем говорить, что функция f(x,y) удоволетворяет условию Липшица на D относительно y, если существует постоянная L такая, что

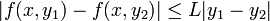
для всех 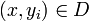, i=1,2.

Пусть правая часть f(x,y) дополнительно удовлетворяет условию Липшица на D относительно y, тогда задача Коши не может иметь в D более одного решения.

Также отметим, что хотя эта теорема имеет глобальный характер, тем не менее она не устанавливает существование глобального решения.

Для существования глобального решения необходимо наложить условия на рост правой части по y: пусть функция f удовлетворяет условию

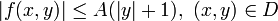
где A>0 - константа не зависящая ни от x, ни от y, тогда задача Коши имеет решение в D. В частности, из этой теоремы следует, что задача Коши для линейных уравнений (с непрерывными по x коэффициентами) имеет глобальное решение.

Теорема существования и единственности решения задачи Коши для номального уравнения первого порядка.

Нормальная система в векторных обозначениях примет вид

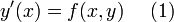
где .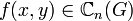

Определение. Вектор-функция 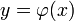называется решением нормальной системы (1) на промежутке 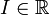, если:

1.

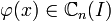
2.

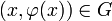
3.

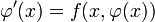
Рассмотрим начальное условие

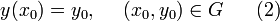
Точка (x₀,y₀) называется начальной точкой, а ее координаты x₀,y₀ называются начальными данными.

Определение. Задача нахождения решения нормальной системы (1), удовлетворяющего начальному условию (2), называется задачей Коши.

Система уравнений вида

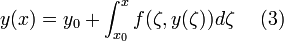
где 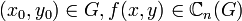, назыается системой интегральных уравнений.

Вектор-функция 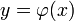называется решением на промежутке 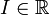системы (3), если:

1.

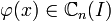
2.

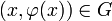
3.

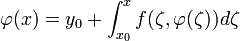
Лемма об эквивалентности. Вектор-функция 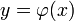- решение задачи Коши (1) при условии (2) тогда и только тогда, когда 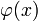решение системы интегральных уравнений (3).