Методика выполнения расчётно-графической работы №1

Расчётно-графическая работа содержит 4 раздела.

В первом разделе:

1. Формулируется тема;

2. Формулируется цель работы.

Во втором разделе:

1. Формулируется условие задачи (в зависимости от специализации);

2. Заполняется таблица исходных данных выборки по результатам экспериментов, проведённых со спортсменами одной специализации.

В третьем разделе:

1. Результаты измерений представляются в виде вариационного ряда;

2. Даётся графическое представление вариационного ряда.

3. Формулируется вывод.

В четвёртом разделе:

1. Рассчитываются основные статистические характеристики ряда измере-ний;

2. По итогам расчётов формулируется вывод.

Оформление работы:

1. Работа выполняется в отдельной тетради или на форматных листах.

2. Титульный лист заполняется по образцу.

(Пример оформления титульного листа)

Российский Государственный Университет

физической культуры, спорта, молодёжи и туризма

Кафедра естественнонаучных дисциплин

Графическое представление результатов экспериментов

Расчёт основных статистических характеристик

Расчётно-графическая работа №1

по курсу математики

Выполнил: студент 1 к. 1 пот. 1гр.

Иванов С.М.

Преподаватель : доц. кафедры ЕНД и ИТ

(Ф.И.О.)

Москва - 2012

Пример выполнения расчётно-графической работы №1.

Пример

Тема работы: Графическое представление результатов эксперимента. Расчёт основных статистических характеристик.

Цель работы: Научиться представлять результаты исследований в графическом виде и определять основные статистические характеристики.

Условие задачи: 18 спортсменов выполняли прыжки в длину. Результаты длины прыжка Y_i (м) занесены в таблицу.

Таблица исходных данных выборки:

Таблица 3

№ п/п
Yi, м	6,35	6,83	6,25	6,38	6,42	6,35	6,51	6,06	6,22
ранжированная выборка	6,00	6,06	6,18	6,20	6,22	6,25	6,35	6,35	6,38
№ п/п
Yi, м	6,20	6,00	6,50	6,65	6,55	6,75	6,60	6,18	6,55
ранжированная выборка	6,42	6,50	6,51	6,55	6,55	6,60	6,65	6,75	6,83

Определим число интервалов по формуле Стерджеса

.

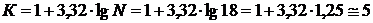Определим шаг (или ширину) интервала по формуле:

,

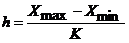где 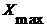- максимальное значение измеряемого показателя в упорядоченной (ранжированной) выборке; 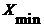- минимальное значение показателя.

Определим шаг или ширину интервала

.

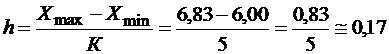Границу интервала обычно округляют в большую сторону до размерности измеряемого показателя. Нижнюю границу первого интервала выберем равной минимальному значению выборки, то есть 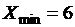. Заполним таблицу по результатам выборки (см. табл. 6), которые распределены в интервалы, т. е. результаты измерений представим в виде вариационного ряда.

В первый столбец таблицы впишем номера 5 интервалов.

Во второй столбец – границы интервала. Нижней границей первого интервала выбрали 6, прибавим к ней шаг и получим верхнюю границу первого интервала (6,00+0,17=6,17). Этот же результат является нижней границей следующего интервала (6,17+0,17=6,34) и т. д.

Значение верхней границы последнего интервала 6,85 больше максимального значения показателей выборки 6,83.

Третий столбец – срединные значения интервалов. Середину первого интервала определим как среднее арифметическое значение его границ. Середины следующих интервалов получим прибавлением шага интервала к предыдущим значениям.

Четвертый столбец – частота (n_i), т. е. количество значений, попавших в заданный интервал. Если граничный результат был учтен в интервале, то в последующем интервале учитываются значения выше граничного результата.

Пятый столбец – накопленная частота рассчитывается суммированием частот предыдущих интервалов. В последней строке столбца 4 получилось число, равное объему выборки (14).

Шестой столбец – частость (р_i^*) рассчитывается делением частоты на объём выборки.

Седьмой столбец – накопленная частость получается суммированием частостей предыдущих интервалов. В последней строке столбца 7 получилась единица.

Распределение измерений, представленное в столбцах 2(границы интервалов) и 4(частота) или 2(границы интервалов) и 6(частость), назы­вается вариационным рядом. Напомним, что интервальным вариационным рядом называется упорядоченная совокуп­ность интервалов варьирования случайной величины с соответствующими часто­тами или частостями попаданий в каждый из них значений величины.

Представим результаты измерений в виде вариационного ряда (табл. 7).

Таблица 4

Результаты измерений, представленные в виде вариационного ряда

№ интервала	Границы интервала	Срединное значение интервала	Частота ni	Накопленная частота	Частость рi*	Накопленная частость
	6,00 – 6,17	6,085			2/18	2/18
	6,17 – 6,34	6,255		6(2+4)	4/18	6/18
	6,34 – 6,51	6,425		12(6+6)	6/18	12/18
	6,51 – 6,68	6,595		16(12+4)	4/18	16/18
	6,68 – 6,85	6,765		18(16+2)	2/18	18/18=1