Отличия евклидовой и неевклидовой геометрии

Реферат

На тему: «Неевклидова геометрия – ее возникновение и философское значение»

Выполнила студентка 1 курса, группы 177мШведова Анна Сергеевна

Приняла: СеливерстоваНинаАндреевна

Санкт-Петербург

Содержание

Введение. 3

1 История развития геометрии. 5

2 Отличия евклидовой и неевклидовой геометрии. 8

3 Неевклидова геометрия и развитие философии математики в XIX веке. 11

3.1 Развитие философии математики в XIX веке. 12

3.2 Философское значение открытия неевклидовой геометрии. 14

3.3 Мифы о геометрии Лобачевского и их опровержение. 16

Заключение. 18

Список используемой литературы.. 20

Введение

Значимость математики в современной науке постоянно возрастает. Математика – чрезвычайно своеобразная наука, философский анализ целого ряда положений которой весьма сложен. И хотя особенности математического знания были предметом пристального внимания выдающихся философов и математиков всех времен и народов, многие методологические проблемы математики остаются недостаточно разработанными, что в свою очередь тормозит развитие как «чистой» и прикладной математики, так и других отраслей науки, в том числе философии.

Философия в сфере математики способствует выработке адекватного понимания математического знания, решению естественно возникающих вопросов о предмете и методах математики, специфике ее понятий. Действительно философское понимание математики может предстать только как сумма выводов, сумма определений, полученных на основе анализа различных ее сторон. Правильное понимание математики не может быть получено умозрительно или путем простого сравнения случаев, которые подходят под известное интуитивное представление, и подыскания затем некоторых объединяющих их признаков. Такой метод необходим для предварительного понимания любого предмета, но сам по себе он недостаточен.

Как наука, геометрия впервые сформировалась в Древней Греции, когда геометрические закономерности и зависимости, найденные ранее опытным путем, были приведены в надлежащую систему и доказаны.

В III веке до нашей эры греческий ученый Евклид привел в систему известные ему геометрические сведения в большом сочинении «Начала». Эта книга более двух тысяч лет служила учебником геометрии во всем мире.“Начала” состоят из 13 книг, посвященных геометрии и арифметике в геометрическом изложении[1].

Открытие неевклидовой геометрии произвело переворот не только в геометрии и даже не только в математике, но можно сказать, в развитии человеческого мышления вообще. И то, что евклидова геометрия не является единственно возможной, сделанное в начале прошлого века Гауссом, Лобачевским и Больяи, оказало влияние на мировоззрение человечества. Однако мало кому известно, что начиная с конца прошлого века неевклидова геометрия, наряду с евклидовой, является одним из рабочих инструментов математики, несмотря на то что «пространство, в котором мы живем», в доступных нашему пониманию пределах является скорее евклидовым, чем неевклидовым.

История развития геометрии

Одни из первых понятий в геометрии люди приобрели еще в глубокой древности. Возникала необходимость определять площади участков земли, объемы различных сосудов и помещений и другие практические потребности. Свое начало история развития геометрии, как науки, берет в Древнем Египте около 4 тысяч лет назад. Затем знания египтян позаимствовали древние греки, которые применяли их преимущественно для того, чтобы измерять площади земельных участков. Именно с Древней Греции берет свое начало история возникновения геометрии, как науки. Древнегреческое слово «геометрия» переводится, как «землемерие».

Греческие ученые на основе открытия множества геометрических свойств смогли создать стройную систему знаний по геометрии. В основу геометрической науки были положены простейшие геометрические свойства, взятые из опыта. Остальные положения науки выводились из простейших геометрических свойств с помощью рассуждений. Вся эта система была опубликована в завершенном виде в «Началах» Евклида около 300 года до нашей эры, где он изложил не только теоретическую геометрию, но и основы теоретической арифметики. С этого источника также начинается и история развития математики.

Стоит отметить, что в своем труде Евклид ничего не сказал ни об измерении объема, ни о поверхности шара, ни об отношении длины круга к его диаметру. История развития геометрии получила продолжение в середине III века до нашей эры благодаря великому Архимеду (287 до н. э. — 212 до н. э.), который смог вычислить всем нам хорошо известное число Пи, а также смог определить способы вычисления поверхности шара. Архимед для решения упомянутых задач применил методы, которые в дальнейшем легли в основу методов высшей математики. С их помощью он уже мог решать трудные практические задачи геометрии и механики, которые были важны для мореплавания и для строительного дела. В частности, он нашел способы определять центры тяжести и объемы многих физических тел и смог изучить вопросы равновесия тел различной формы при погружении в жидкость[2].

Древнегреческие ученые провели исследования свойств различных геометрических линий, важных для теории науки и практических применений. Аполлоний(262 до н. э. — 190 до н. э.)сделал много важных открытии по теории конических сечений, которые оставались непревзойденными на протяжении следующих восемнадцати веков. Апполоний применил метод координат для изучения конических сечений. Этот метод в дальнейшем смогли развить только в XVII веке ученые Ферма и Декарт. Но они применяли этот метод только для изучения плоских линий. И только в 1748 году русский академик Эйлер смог применить этот метод для изучения кривых поверхностей.

Система, разработанная Евклидом, считалась непреложной более двух тысяч лет. Важнейшим недостатком системы евклидовых аксиом, включая и его постулаты, является ее неполнота, то есть недостаточность их для строго логического построения геометрии, при котором каждое предложение, если оно не фигурирует в списке аксиом, должно быть логически выведено из последних. Поэтому Евклид при доказательстве теорем не всегда основывался на аксиомах, а прибегал к интуиции, к наглядности и «чувственным» восприятиям. Например, понятию «между» он приписывал чисто наглядный характер; он молчаливо предполагал, что прямая, проходящая через внутреннюю точку окружности, непременно должна пересечь ее в двух точках. При этом он основывался только на наглядности, а не на логике; доказательства этого факта он нигде не дал, и дать не мог, так как у него отсутствовали аксиомы непрерывности.

Критика евклидовского обоснования геометрии, продолжавшаяся на протяжении нескольких веков и ставшая особенно острой в 19 столетии, привела к попыткам нового дедуктивного построения геометрии, отвечающего современным требованиям науки.

Одним из ученых, предвосхитивших неевклидову геометрию, был итальянский монах Джироламо Саккери (1667-1733). На последнем году своей жизни Саккери опубликовал (на латинском языке) книгу под заглавием «Евклид, очищенный от всех пятен». В ней он поставил перед собой задачу исправить все недостатки («пятна») «Начал» Евклида. Саккери решительнее и дальше своих предшественников сделал попытку доказать пятый постулат от противного. Этот путь он не сумел проделать до конца, но идя по нему, Лобачевский впоследствии открыл неевклидову геометрию.

История развития геометрии получила неожиданный поворот, когда в 1826 году гениальный русский математик Н.И. Лобачевский смог создать совершенно новую геометрическую систему. Фактически основные положения его системы отличаются от положений геометрии Евклида только в одном пункте, но именно из этого пункта вытекают основные особенности системы Лобачевского. Это положение о том, что сумма углов треугольника в геометрии Лобачевского всегда меньше 180 градусов. На первый взгляд может показаться, что это утверждение неверно, однако при маленьких размерах треугольников современные средства измерения не дают правильно измерить сумму его углов.

Дальнейшая история развития геометрии доказала правильность гениальных идей Лобачевского и показала, что система Евклида просто неспособна решить многие вопросы астрономии и физики, где математики имеют дело с фигурами практически бесконечных размеров. Именно с трудами Лобачевского уже связано дальнейшее развитие геометрии, а с ней и высшей математики и астрономии.

Заключение

Открытия в науке, как бы они не были велики, сами по себе не являются вкладом в философию, однако существуют открытия, которые влекут за собой изменения в философии науки, в понимании ее предмета, методов, связи с другими науками. Неевклидовы геометрии – пример одного из таких открытий, чрезвычайно редких в истории науки. До построения неевклидовых геометрий к таким сдвигам в математике, имевшим философское значение, можно отнести только три события, а именно появления самой идеи математики как дедуктивной науки, открытие несоизмеримых величин и открытие дифференциального исчисления.

Открытие неевклидовой геометрии, начало которому положил Лобачевский, не только сыграло огромную роль в развитии новых идей и методов в математике естествознании, но имеет и философское значение. Господствовавшее до Лобачевского мнение о незыблемости геометрии Евклида в значительной мере основывалось на учении известного немецкого философа И. Канта, родоначальника немецкого классического идеализма. Кант утверждал, что человек упорядочивает явления реального мира согласно априорным представлениям, а геометрические представления и идеи якобы априорны (латинское слово aprior означает – изначально, заранее), то есть, не отражают явлений действительного мира, не зависят от практики, от опыта, а являются врожденными человеческому миру, раз и навсегда зафиксированными, свойственными человеческому разуму, его духу. Поэтому, Кант считал, что Евклидова геометрия непоколебима, неизменна, и является вечной истиной. Еще до Канта геометрия Евклида считалась незыблемой, как единственно возможное учение о реальном пространстве.

Открытие неевклидовой геометрии доказало, что нельзя абсолютировать представления о пространстве, что «употребительная» (как назвал Лобачевский геометрию Евклида) геометрия не является единственно возможной, однако это не подорвало незыблемость геометрии Евклида. Итак, в основе геометрии Евклида лежат не априорные, врожденные уму понятия и аксиомы, а такие понятия, которые связаны с деятельностью человека, с человеческой практикой. Только практика может решить вопрос о том, какая геометрия вернее излагает свойства физического пространства. Открытие неевклидовой геометрии дало решающий толчок грандиозному развитию науки, способствовало и поныне способствует более глубокому пониманию окружающего нас материального мира.

Список используемой литературы

Геометрия Лобачевского [Электронный ресурс] / К. Д. Бокова [и др.] // Юный ученый. – 2016. – №6. – С. 13-15. – Режим доступа: http://yun.moluch.ru/archive/9/626/. ­–Загл. с экрана.

Канке, В. А. Философия математики, физики, химии, биологии/В. А. Канке. – М. :КноРус, 2010.– 368 с.

Панов, В. Ф. Современная математика и её творцы / В. Ф.Панов. – М. : Изд-во МГТУ, 2011. – 648 с.

Паньженский, В. И.Различные варианты построения евклидовой геометрии :
учеб.пособие / В. И. Паньженский, М. В. Сорокина, Н. А. Тяпин. –­ Пенза : Изд-во ПГУ, 2015. – 60 с.

Рыбников, К. А. История математики / К. А.Рыбников. – М. : Изд-во МГУ, 2012. – 456 c.

Светлов, В. А. Философия математики. Основные программы обоснования математики ХХ столетия / В. А.Светлов. – М. :КомКнига, 2010. – 208 c.

Сосов, Е.Н. Геометрия Лобачевского и её применение в специальной теории относительности / Е.Н. Сосов. – Казань: Казан.ун-т, 2016. - 84 с.

Сухотин, А.К. Философия математики : учеб.пособие / А.К. Сухотин. – Томск : Томский ун-т, 2004. – 230 с.

[1]Рыбников, К. А. История математики / К. А. Рыбников. – М. : Изд-во МГУ, 2012. – 456 c.

[2]Паньженский, В. И. Различные варианты построения евклидовой геометрии : учеб.пособие / В. И. Паньженский, М. В. Сорокина, Н. А. Тяпин. –­ Пенза : Изд-во ПГУ, 2015. – 60 с.

[3]Сосов, Е.Н. Геометрия Лобачевского и её применение в специальной теории относительности / Е.Н. Сосов. – Казань: Казан.ун-т, 2016. - 84 с.

[4]Геометрия Лобачевского [Электронный ресурс] / К. Д. Бокова [и др.] // Юный ученый. — 2016. — №6. — С. 13-15. - Режим доступа: http://yun.moluch.ru/archive/9/626/. - Загл. с экрана.(дата обращения 29.10.17.)

[5]Панов, В. Ф. Современная математика и её творцы / В. Ф. Панов. – М. : Изд-во МГТУ, 2011. – 648 с.

[6]Сухотин, А.К. Философия математики : учеб.пособие / А.К. Сухотин. – Томск : Томский ун-т, 2004. – 230 с.

[7]Светлов, В. А. Философия математики. Основные программы обоснования математики ХХ столетия / В. А.Светлов. – М. :КомКнига, 2010. – 208 c.

[8]Канке, В. А.Философия математики, физики, химии, биологии /В. А. Канке. – М. :КноРус, 2010. – 368 с.

Реферат

На тему: «Неевклидова геометрия – ее возникновение и философское значение»

Выполнила студентка 1 курса, группы 177мШведова Анна Сергеевна

Приняла: СеливерстоваНинаАндреевна

Санкт-Петербург

Содержание

Введение. 3

1 История развития геометрии. 5

2 Отличия евклидовой и неевклидовой геометрии. 8

3 Неевклидова геометрия и развитие философии математики в XIX веке. 11

3.1 Развитие философии математики в XIX веке. 12

3.2 Философское значение открытия неевклидовой геометрии. 14

3.3 Мифы о геометрии Лобачевского и их опровержение. 16

Заключение. 18

Список используемой литературы.. 20

Введение

Значимость математики в современной науке постоянно возрастает. Математика – чрезвычайно своеобразная наука, философский анализ целого ряда положений которой весьма сложен. И хотя особенности математического знания были предметом пристального внимания выдающихся философов и математиков всех времен и народов, многие методологические проблемы математики остаются недостаточно разработанными, что в свою очередь тормозит развитие как «чистой» и прикладной математики, так и других отраслей науки, в том числе философии.

Философия в сфере математики способствует выработке адекватного понимания математического знания, решению естественно возникающих вопросов о предмете и методах математики, специфике ее понятий. Действительно философское понимание математики может предстать только как сумма выводов, сумма определений, полученных на основе анализа различных ее сторон. Правильное понимание математики не может быть получено умозрительно или путем простого сравнения случаев, которые подходят под известное интуитивное представление, и подыскания затем некоторых объединяющих их признаков. Такой метод необходим для предварительного понимания любого предмета, но сам по себе он недостаточен.

Как наука, геометрия впервые сформировалась в Древней Греции, когда геометрические закономерности и зависимости, найденные ранее опытным путем, были приведены в надлежащую систему и доказаны.

В III веке до нашей эры греческий ученый Евклид привел в систему известные ему геометрические сведения в большом сочинении «Начала». Эта книга более двух тысяч лет служила учебником геометрии во всем мире.“Начала” состоят из 13 книг, посвященных геометрии и арифметике в геометрическом изложении[1].

Открытие неевклидовой геометрии произвело переворот не только в геометрии и даже не только в математике, но можно сказать, в развитии человеческого мышления вообще. И то, что евклидова геометрия не является единственно возможной, сделанное в начале прошлого века Гауссом, Лобачевским и Больяи, оказало влияние на мировоззрение человечества. Однако мало кому известно, что начиная с конца прошлого века неевклидова геометрия, наряду с евклидовой, является одним из рабочих инструментов математики, несмотря на то что «пространство, в котором мы живем», в доступных нашему пониманию пределах является скорее евклидовым, чем неевклидовым.

История развития геометрии

Одни из первых понятий в геометрии люди приобрели еще в глубокой древности. Возникала необходимость определять площади участков земли, объемы различных сосудов и помещений и другие практические потребности. Свое начало история развития геометрии, как науки, берет в Древнем Египте около 4 тысяч лет назад. Затем знания египтян позаимствовали древние греки, которые применяли их преимущественно для того, чтобы измерять площади земельных участков. Именно с Древней Греции берет свое начало история возникновения геометрии, как науки. Древнегреческое слово «геометрия» переводится, как «землемерие».

Греческие ученые на основе открытия множества геометрических свойств смогли создать стройную систему знаний по геометрии. В основу геометрической науки были положены простейшие геометрические свойства, взятые из опыта. Остальные положения науки выводились из простейших геометрических свойств с помощью рассуждений. Вся эта система была опубликована в завершенном виде в «Началах» Евклида около 300 года до нашей эры, где он изложил не только теоретическую геометрию, но и основы теоретической арифметики. С этого источника также начинается и история развития математики.

Стоит отметить, что в своем труде Евклид ничего не сказал ни об измерении объема, ни о поверхности шара, ни об отношении длины круга к его диаметру. История развития геометрии получила продолжение в середине III века до нашей эры благодаря великому Архимеду (287 до н. э. — 212 до н. э.), который смог вычислить всем нам хорошо известное число Пи, а также смог определить способы вычисления поверхности шара. Архимед для решения упомянутых задач применил методы, которые в дальнейшем легли в основу методов высшей математики. С их помощью он уже мог решать трудные практические задачи геометрии и механики, которые были важны для мореплавания и для строительного дела. В частности, он нашел способы определять центры тяжести и объемы многих физических тел и смог изучить вопросы равновесия тел различной формы при погружении в жидкость[2].

Древнегреческие ученые провели исследования свойств различных геометрических линий, важных для теории науки и практических применений. Аполлоний(262 до н. э. — 190 до н. э.)сделал много важных открытии по теории конических сечений, которые оставались непревзойденными на протяжении следующих восемнадцати веков. Апполоний применил метод координат для изучения конических сечений. Этот метод в дальнейшем смогли развить только в XVII веке ученые Ферма и Декарт. Но они применяли этот метод только для изучения плоских линий. И только в 1748 году русский академик Эйлер смог применить этот метод для изучения кривых поверхностей.

Система, разработанная Евклидом, считалась непреложной более двух тысяч лет. Важнейшим недостатком системы евклидовых аксиом, включая и его постулаты, является ее неполнота, то есть недостаточность их для строго логического построения геометрии, при котором каждое предложение, если оно не фигурирует в списке аксиом, должно быть логически выведено из последних. Поэтому Евклид при доказательстве теорем не всегда основывался на аксиомах, а прибегал к интуиции, к наглядности и «чувственным» восприятиям. Например, понятию «между» он приписывал чисто наглядный характер; он молчаливо предполагал, что прямая, проходящая через внутреннюю точку окружности, непременно должна пересечь ее в двух точках. При этом он основывался только на наглядности, а не на логике; доказательства этого факта он нигде не дал, и дать не мог, так как у него отсутствовали аксиомы непрерывности.

Критика евклидовского обоснования геометрии, продолжавшаяся на протяжении нескольких веков и ставшая особенно острой в 19 столетии, привела к попыткам нового дедуктивного построения геометрии, отвечающего современным требованиям науки.

Одним из ученых, предвосхитивших неевклидову геометрию, был итальянский монах Джироламо Саккери (1667-1733). На последнем году своей жизни Саккери опубликовал (на латинском языке) книгу под заглавием «Евклид, очищенный от всех пятен». В ней он поставил перед собой задачу исправить все недостатки («пятна») «Начал» Евклида. Саккери решительнее и дальше своих предшественников сделал попытку доказать пятый постулат от противного. Этот путь он не сумел проделать до конца, но идя по нему, Лобачевский впоследствии открыл неевклидову геометрию.

История развития геометрии получила неожиданный поворот, когда в 1826 году гениальный русский математик Н.И. Лобачевский смог создать совершенно новую геометрическую систему. Фактически основные положения его системы отличаются от положений геометрии Евклида только в одном пункте, но именно из этого пункта вытекают основные особенности системы Лобачевского. Это положение о том, что сумма углов треугольника в геометрии Лобачевского всегда меньше 180 градусов. На первый взгляд может показаться, что это утверждение неверно, однако при маленьких размерах треугольников современные средства измерения не дают правильно измерить сумму его углов.

Дальнейшая история развития геометрии доказала правильность гениальных идей Лобачевского и показала, что система Евклида просто неспособна решить многие вопросы астрономии и физики, где математики имеют дело с фигурами практически бесконечных размеров. Именно с трудами Лобачевского уже связано дальнейшее развитие геометрии, а с ней и высшей математики и астрономии.

Отличия евклидовой и неевклидовой геометрии

Основным пунктом, откуда начинается разделение геометрии на обычную евклидову («употребительную» по терминологии Лобачевского) и неевклидову («воображаемую» геометрию или «пангеометрию», по его же терминологии), является, как известно, постулат о параллельных линиях[3].

В основе обычной геометрии лежит предположение (аксиома, постулат), что через точку, не лежащую на данной прямой, можно провести в плоскости, определяемой этой точкой и прямой, не более одной прямой, не пересекающей данную прямую. Прямая ВВ' (рис. 1), проходящая через точку Р под прямым углом к перпендикуляру PQ, опущенному на АА', не пересекает прямой АА'; эта прямая в евклидовой геометрии, и называется параллельной к АА'.

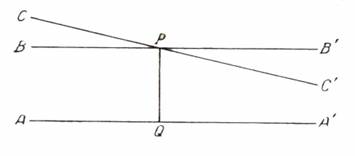
Рисунок 1 – Пятый постулат евклидовой геометрии

В противоположность постулату Евклида, Лобачевский принимает в основу построения теории параллельных линий следующую аксиому: через точку, не лежащую на данной прямой, можно провести в плоскости, определяемой этой точкой и прямой, более одной прямой, не пересекающей данную прямую.

Отсюда непосредственно вытекает существование бесконечного множества прямых, проходящих через одну и ту же точку и не пересекающих данную прямую. Пусть прямая CC' не пересекает АА'; тогда все прямые, проходящие внутри двух вертикальных углов: ВРС и В'РС', также не пересекаются с прямой АА'.

Из постулата Лобачевского непосредственно вытекает, что через точку Р, не лежащую на данной прямой АА' (рис.2), в плоскости, ими определяемой, можно провести бесчисленное множество прямых, не пересекающих АА'. Существуют две граничные прямые СС' и DD', разделяющие класс пересекающих прямых, лежащих в углах CPD и C'PD', от класса не пересекающих, проходящих внутри углов CPD' и DPC'. Эти прямые не пересекают прямую АА'. Прямые СС' и DD' Лобачевский и называет параллельными прямой АА' в точке P.

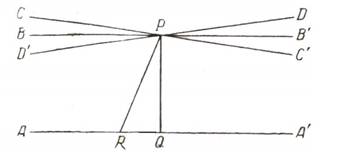
Рисунок 2 – Параллельные прямые по Лобачевскому

Таким образом, через каждую точку Р плоскости проходят две прямые, параллельные данной: прямая DD', параллельная АА' в направлении А'А, и прямая СС', параллельная той же прямой в противоположном направлении АА'. Обе эти прямые расположены симметрично относительно перпендикуляра PQ, опущенного на АА'. Угол C'PQ Лобачевский называет углом параллельности. Он является функцией длины перпендикуляра PQ, которую Лобачевский назвал так: ∠ C'PQ=П(PQ). Лобачевский показал, что с увеличением длины отрезка PQ угол параллельности уменьшается.

В геометрии Лобачевского критерий параллельности выражается более сложно, чем в евклидовой геометрии. Чтобы доказать, что, например, прямая СС' в точке Р параллельна АА' в направлении АА', необходимо: 1) установить факт непересечения этих прямых, 2) показать, что СС' в точке Р является граничной прямой; это последнее устанавливается обычно так («критерий угла»): проводим прямую PR, пересекающую АА', и рассматриваем угол C'PR, который своим отверстием обращен в сторону параллельности; если каждый луч, имеющий вершину в точке Р и проходящийвн утри этого угла, пересекает л уч RA', т о п рямая СС' параллельна АА' в т очке Р в направлении АА'.

Основное свойство параллелизма: Н. И. Лобачевский доказывает, что прямая, параллельная данной прямой в некоторой своей точке, параллельна ей во всех своих точках[4].

В последние годы жизни Лобачевский безуспешно пытался доказать непротиворечивость своей геометрии.

Чтобы получить такое доказательство, надо было построить модель геометрии. В 1868 году (через 12 лет после смерти Лобачевского) итальянский ученый Э. Бельтрами исследовал вогнутую поверхность называемую псевдосферой и доказал, что на этой поверхности действует геометрия Лобачевского.

Также доказательством геометрии Лобачевского являются такие модели как: модели Клейна, модель Пуанкаре[5].