Опр. линейной независимости векторов.

Система векторов 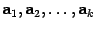называется линейно независимой, если равенство 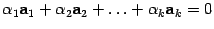возможно только при .

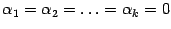Теоремы о линейной зависимости векторов.

Т1. Если в сист. х1,…хn хоть один элемент равен нулю, то система линейно-зависима.

Д-во: сост. лин. комб., которая будет нетрив. и равно нулю.

Пусть х1=0, тогда @1=12, @2=@3=@n=0

@1*x1(=0)+….=0

Т2. Если система х1..хn содержит лин-зав. подсистему х1..хm (m<n), то исходная система тоже линейно-зависима.

Базис в пространстве. Декартов базис.

Если векторы 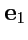, , 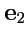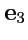взаимно ортогональны и по модулю равны единице, то они называются ортами прямоугольной декартовой системы координат, а сам базис ортонормированным декартовым базисом. Орты декартовой системы координат обычно обозначают как , , .

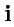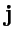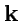Тройка векторов наз. ПРАВОЙ, если с конца в.С поворот по наим.углу от в. А к в.Б видел против час.стрелки.

Декартова система координат

-наз. совокупность фиксированной точки и ортонормированного базиса.

ОМ- радиус-вектор ДСМ

Проекция вектора на ось.

Ось-прямая линия с указ. на ней направлением и с нач.отсчета

Прокцией вект.а на ось l – длина вект.а, начало и конец которого получены с помощью проектирования на ось l начала и конца а.
Если проекция а и ось колл., то проекция «+»

Если неколлинеарны, то проекция с «-».

Углы, образ а и осями. Кос этих углов- направляющие косинусы.( являются координатами ортовектора).

Геом. смысл координат вектора.

Геометрический смысл линейной зависимости 2-х векторов

Система векторов и линейно зависима тогда и только тогда, когда эти векторы коллинеарны.

Пусть система векторов , } линейно зависима, докажем, что || .

По свойству хотя бы один из векторов или выражается через другой, пусть = α, но это в силу определения коллинеарных векторов приводит к коллинеарности векторов || .

Геометрический смысл линейной зависимости трёх векторов.

Система векторов и линейно зависима тогда и только тогда, когда эти векторы компланарны.

Доказательство.

1.Прямо.

Пусть система , и линейно зависима. Докажем, что , и - компланарны.

В силу линейной зависимости имеем α +β +γ = , причем хотя бы одно из

α,β,γ ≠ 0. ( * )

Если хотя бы один из α,β,γ = 0, то получим, например в случае γ = 0: α +β = , т.е.

= - т.е. по теореме 8 следует, что || , но тогда , и - компланарны.

Пусть α ≠ β ≠ γ ≠ 0 . Отложим от точки O вектор = α, затем от А вектор = β, тогда

α + β = .

В силу ( * ): = - γ .

Через точки O, A и B проходит плоскость (OAB).

Т.к. α ≠ β ≠ γ ≠ 0, то из равенств = α, = β и = - γ следует, что , и ей параллельны, т.е. они компланарны.

Можно доказать и обратное.

11) Линейной зависимость4х векторов

Теорема о линейной зависимости 4-х векторов:векторы 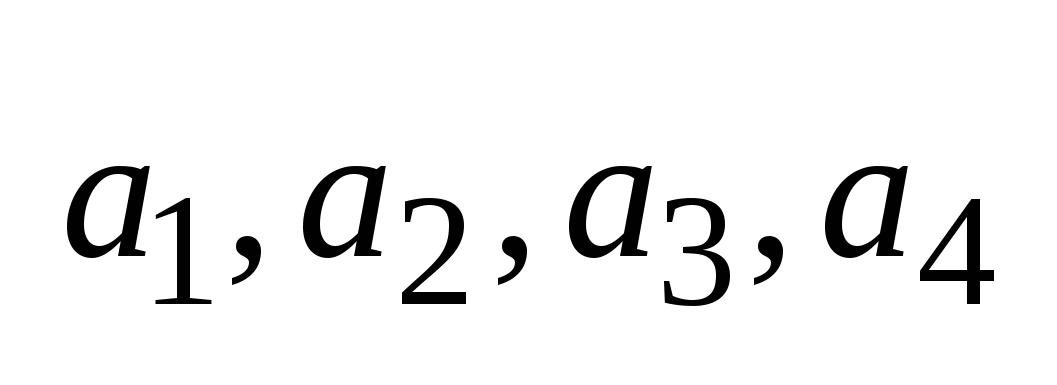линейно зависимы в пространстве.

Доказательство: а) 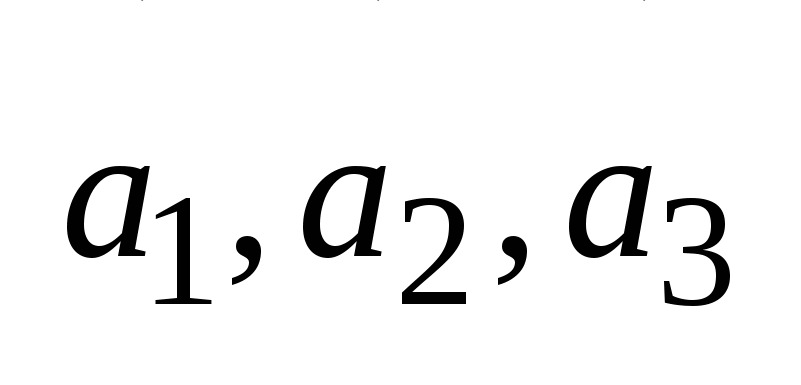- некомпланарны, тогда по лемме 2 о разложении 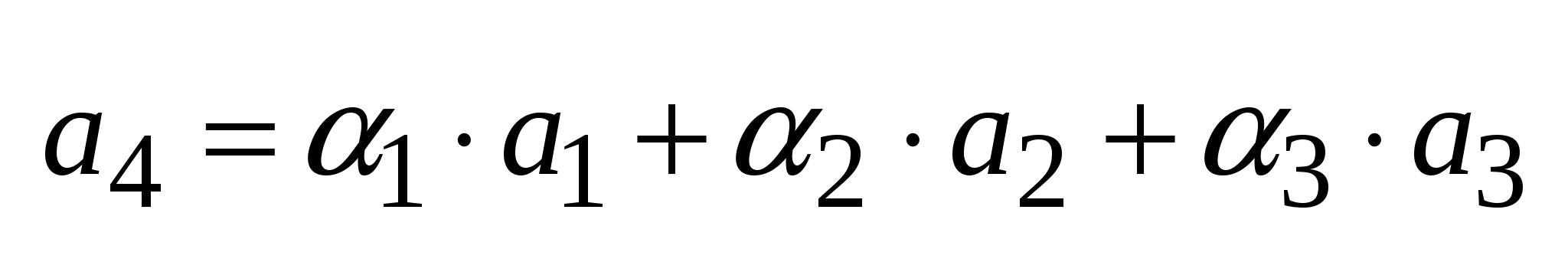, то по критерию о линейной зависимости 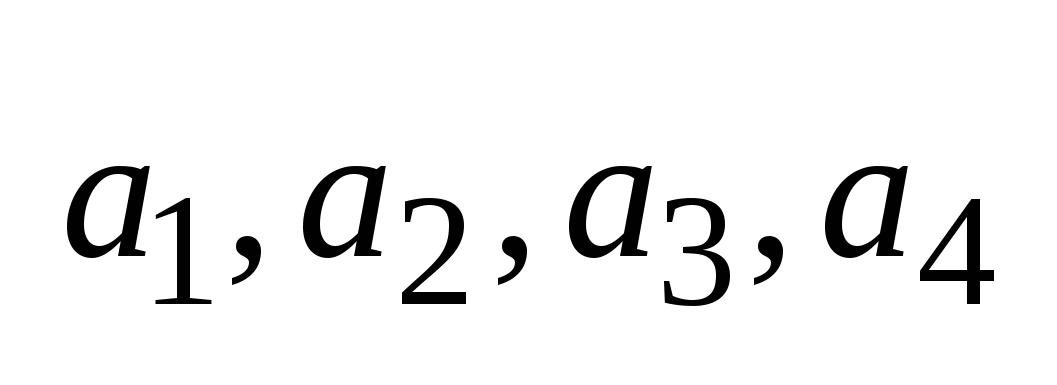линейно зависимы. б) 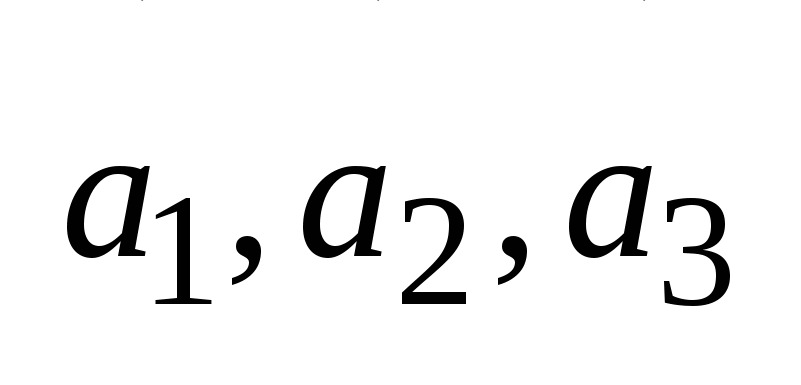- компланарны, тогда по теореме о линейной зависимости 3-х векторов 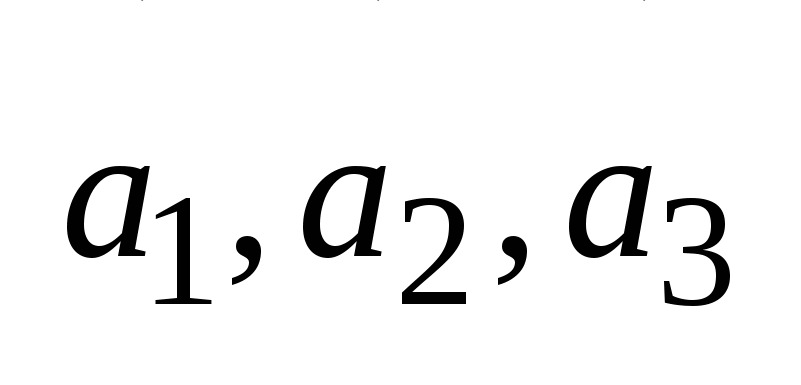- линейно зависимы, тогда по теореме о линейно зависимой подсистеме 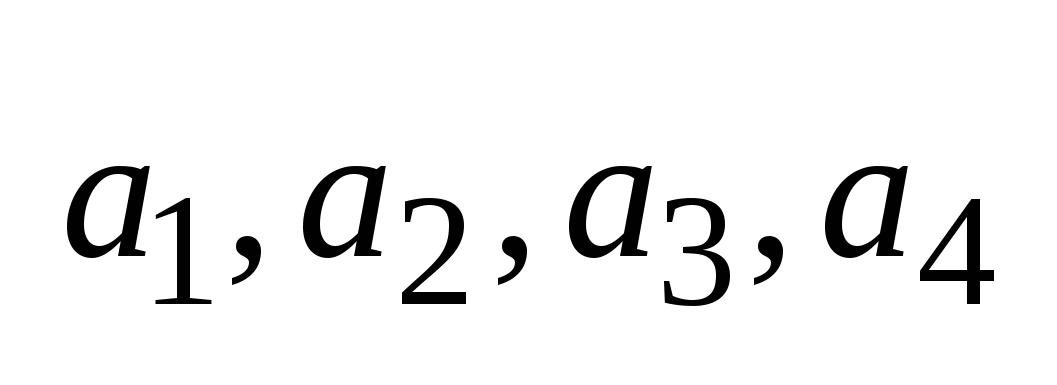линейно зависимы.