Определение обратной матрицы. Условие существования обратной матрицы. Формула нахождения обратной матрицы.

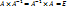Матрица называется обратной матрице А, если выполняется условие , где Е – единичная матрица того же порядка, что и матрица А. Матрица имеет те же размеры, что и матрица А. Понятие обратной матрицы распространяется только на квадратные матрицы. Квадратная матрица, определитель которой отличен от нуля, называется невырожденной.

Квадратная матрица, определитель которой равен нулю, называется вырожденной.

Союзная матрица: , где – алгебраическое дополнение элемента ij данной матрицы.

Условие существования обратной матрицы. Лемма: Если А – квадратная матрица n-ого порядка, – союзная к ней матрица, то 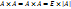, где Е – единичная матрица n-ого порядка.

Доказательство: Рассмотрим произведение матрицы А и При вычислении элементов матрицы произведения, стоящих на главной диагонали, будет получаться сумма произведений элементов i-ой строки матрицы А на их алгебраическое дополнение, а это равно определителю. Для получения остальных элементов матрицы надо находить сумму произведений элементов i-ой строки на алгебраическое дополнение элементов j-ой строки, а это согласно 10-ому свойству определителей равно нулю. Аналогично можно доказать, что

Теорема 1, о существовании обратной матрицы. Для того, чтобы существовала матрица , обратная матрице А, необходимо и достаточно, чтобы матрица А была невырожденной.

Доказательство. Необходимость. Пусть матрица А имеет обратную матрицу , тогда 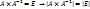. По 9-ому свойству определителей 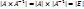. Так как |E|=1, то , следовательно матрица A – невырожденная.

Достаточность. Пусть матрица А – невырожденная, то есть . Докажем, что существует такая матрица , которая является обратной к матрице А и докажем, что такой матрицей является 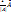, где – союзная матрица к A. Согласно лемме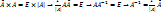

Формула обратной матрицы: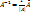

Теорема 2, о единственности обратной матрицы. Для невырожденной матрицы существует единственная обратная матрица.

Доказательство. Пусть существуют матрицы 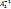и обратные невырожденной матрице А, тогда (слева).

10. Ранг матрицы и его свойства.

Рассмотрим матрицу 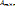. Выделим в ней k строк и k столбцов, где 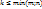, необязательно рядом. Из элементов, стоящих на пересечении выделенных строк и столбцов составить определитель k-ого порядка. Все такие определители называются минорами матрицы (не путать с минорами элементов!!!).

Рангом матрицы А называется наибольший из порядков миноров данной матрицы, отличных от нуля. Обозначается r, r(A), rang.

Из определения следует:

1. Ранг матрицы 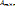не превосходит меньший из ее размеров, то есть .

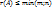2. 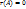, тогда и только тогда, когда все элементы матрицы равны нулю, то есть матрица – нулевая.

3. Для квадратной матрицы n-ого порядка r=n тогда и только тогда, когда матрица А – невырожденная.

Свойства ранга матрицы:

1. При транспонировании ранг матрицы не меняется.

2. Ранг матрицы, полученный из данной вычеркиванием какого-либо ряда, равен рангу данной матрицы или меньше его на единицу.

3. Ранг матрицы, полученный из данной приписыванием к ней ряда, элементами которого являются произвольные числа, равен рангу исходной матрицы или больше его на единицу.

4. Если вычеркнуть из матрицы или прибавить к ней нулевой ряд, то ранг матрицы не меняется.

5. Ранг матрицы не изменяется при элементарных преобразованиях матрицы.

11. (только практика) Способы вычисления ранга.

1 способ, по определению.

2 способ, с помощью приведению к виду трапеции. Ранг равен количеству ненулевых строк.

3 способ. Максимальное число линейно независимых строк/столбцов матрицы равно рангу матрицы.

12.Сформулировать элементарные преобразования матриц. Определение эквивалентных матриц.

Элементарные преобразования матрицы:

1. Отбрасывание нулевого ряда.

2. Умножение всех элементов матрица на число неравное нулю.

3. Перестановка местами двух параллельных рядов матрицы.

4. Прибавление к каждому элементу одного ряда соответствующих элементов параллельного ряда, умноженных на одно и то же число.

Две матрицы называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований. Обозначаются .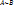

14.Определение системы линейных уравнений (в том числе, что значит решить систему, какие системы называются совместными, определенными и эквивалентными).Сформулировать элементарные преобразования систем.

Системой линейных уравнений, содержащей m уравнений и n неизвестных, называется система вида:

, где числа 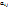– коэффициенты при неизвестных, – свободные члены, – неизвестные или переменные.

Решением системы уравнений называется упорядоченная система чисел 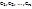при подстановке которой все уравнения системы обращаются в верное равенство.

Решить систему – значит выяснить, совместна ли она или несовместна. Если система совместна – найти все ее решения.

Система уравнений называется совместной, если она имеет хотя бы одно решение и не совместной, если она не имеет решений.

Совместная система называется определенной, если она имеет единственное решение и неопределенной, если она имеет более одного решения.

Системы уравнений называют эквивалентными (равносильными), если они имеют одно и то же множество решений. Эквивалентные системы получаются при элементарных преобразованиях матрицы при условии, что преобразования выполняются лишь над строками матрицы.

Элементарные преобразования систем:

1. Умножение некоторого уравнения системы на число, отличное от нуля.

2. Прибавление к одному уравнению системы другого ее уравнения, умноженного на произвольное число.

3. Перестановка местами двух уравнений системы или слагаемых в уравнениях.

4. Вычеркивание нулевого уравнения.

5. Удаление уравнений, являющимися линейными комбинациями других уравнений системы.

Матрица, состоящая из коэффициентов при неизвестных называется основной матрицей системы.

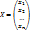– матрица неизвестных; 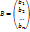– матрица свободных членов; 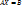– матричная форма записи системы.

13.Определение базисного минора матрицы. Сформулировать теорему о базисном миноре. Следствия из данной теоремы.

Базисным минором матрицы называют отличный от нуля ее минор, порядок которого равен рангу матрицы.

Строки и столбцы, на пересечении которых стоят элементы базисного минора, называют базисными.

Теорема о базисном миноре:

1. Любая строка/столбец матрицы является линейной комбинацией базисных строк/столбцов.

2. Базисные строки/столбцы линейно независимы.

Из теоремы следует: Максимальное число линейно независимых строк/столбцов матрицы равно рангу матрицы.

15.(только практика) Решение системы матричным способом.

Метод обратной матрицы.

Применим только для случая, когда число уравнений равно числу неизвестных.

Основная матрица системы – квадратная порядка n. Определитель этой матрицы называется определителем системы. Если определитель системы отличен от нуля, то матрица А – невырожденная и существует обратная матрица .

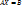
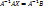
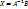, то есть решение системы существует.

Если определитель системы = 0, то система не имеет решения.

16.(только практика) Решение системы методом Крамера.

Применим только для случая, когда число уравнений равно числу неизвестных.

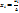, где ∆ - определитель основной матрицы; – определитель, полученный из определителя ∆ заменой i-ого столбца столбцом свободных членов матрицы b.

17.(только практика) Решение системы методом Гаусса.

Применим для решения систем общего вида, содержащих m уравнений и n неизвестных.

Метод Гаусса – метод последовательного исключения переменных. Заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе трапециевидного или треугольного вида (прямой ход), из которого последовательно, начиная с последних по номеру переменных находятся все остальные переменные (обратный ход).

Прямой ход.

1. Составить расширенную матрицу системы. (Расширенная матрица системы получается из основной матрицы приписыванием столбца свободных членов).

2. С помощью элементарных преобразований строк расширенной матрицы приводим ее к трапециевидному или треугольному виду.

3. Если число ненулевых строк преобразованной матрицы равно числу ненулевых строк части матрицы, стоящей слева от вертикальной черты, то система совместна. В противном случае она несовместна.

Обратный ход.

1. Если преобразованная матрица приведена к треугольному виду, то система имеет единственное решение, начиная с последнего ее уравнения последовательно находят значения всех ее неизвестных.

2. Если преобразованная система имеет трапециевидный вид, то система имеет бесконечное множество решений. В этом случае неизвестные называют свободными и формируют правые части уравнений, оставим в левых частях слагаемые, содержащие базисные переменные. Количество базисных переменных равно количеству ненулевых строк трапециевидной матрицы (равно рангу матрицы).