Дать определение арифметической прогрессии и изложить ее свойства.

Билет 45

Арифметическая прогрессия – это последовательность каждый член которой, начиная со 2-го равен предыдущему, сложенному с постоянным числом.

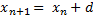
d – Разность прогрессии

1.

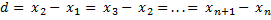
2. 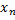– общий член прогрессии

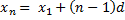
3. Характеристическое свойство прогрессии:

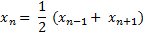
4. Сумма 2-х членов конечной арифметической прогрессии, равностоящих от начала и конца - величина постоянной и равная сумме ее крайних членов.

5. Сумма членов 1-х n арифметической прогрессии равна полу сумме ее крайних членов умноженных на количество членов прогрессии.

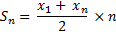
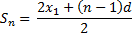
БИЛЕТ

Дать определение геометрической прогрессии и изложить ее свойства.

ГП-Числовая последовательность, первый член которой отличен от нуля, а каждый член, начиная со второго, равен предшествующему, умноженному на одно и тоже отличное от нуля число.
св-ва:
1)Последовательность является геометрической прогрессией тогда и только
тогда, когда для любого n > 1 верно равенство(bn^2=bn-1*bn+1 (n,n-1,n+1 пишешь как нижний префикс.т.е. степень тока снизу)).
2)Квадрат любого (кроме первого) члена геометрической прогрессии равен произведению равноотстоящих от него членов.
3) Каждый член геометр прогрессии начиная со второго равен среднему геометр двух соседних с ним членов

БИЛЕТ

Дать определение числового ряда. Определить понятия сходимости и суммы ряда. Изложить основные свойства рядов.

Числовой ряд – бесконечная сумма членов бесконечной числовой последовательности {an} называется числовым рядом:
a1 + a2+ a3 + … + an+ … = +=∑ nk=1 an
Числовой ряд 1 –назыв.сходящимся, если последовательность его n-х частных сумм имеет предел при n ∞.
Если предел бесконечен или не существует, то ряд расходится.
Св-во рядов:
1) Сходимость ряда не нарушится если все его члены умножить на одно и тоже отличное от нуля число. ( a1+a2+..+an=∑ nk=1 *an=S1 )
2) Сумма (разность) 2 сходящихся рядов есть ряд расходящийся. ( a1+a2+..+an=∑ nk=1 *an=S2 )
Следствие: если ряды 1 и 2 сходятся, то для любых чисел С1 и С2 ряд с общим членом Vn=C1 an -+ C2b2 и их сумма = С1S1 +_ С2S2
3) Сходимость ряда не нарушится если изменить конечное число его членов.
4) Остаток ряда и его свойства: n-м остатком ряда называется ряд полученный из исходного отбрасыванием его первых n-членов . Rn=a1+1+an+t+…=∑ nk=1 –ряд, если ряд сходится, то Rn=S-Sn.
5) Числовой ряд сходится либо расходится одновременно. Если ряд сходится, то сумма n-го остатка 0.

БИЛЕТ

Определите понятие остатка ряда и изложить его свойства. Сформулировать и доказать необходимое условие сходимости числового ряда и его следствие.

48. Остаток ряда и его св-во. n-ым остатком ряда называется рад, полученный из исходного отбрасыванием его 1-ых n-членов. Формула : 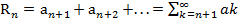. Если сходится, то .
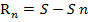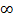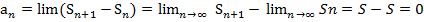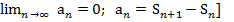
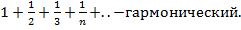
Необходимые условия сходимости. Для того, что бы ряд сходился необходимо, чтобы придел его n-го члена при n- был равен 0. Необходимое условие, если сходится, но не достаточно: lim . [ 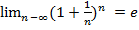-2-ой замечательный придел.

-Следствие из признака сходимости:1)lim 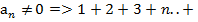-ряд рас? 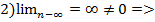- ряд рах?

БИЛЕТ