Теоремы о дифференцируемых функциях
Теорема Ролля. Если функция y= f(x) непрерывна на отрезке [a; b], дифференцируема во всех внутренних точках этого отрезка (т.е. на (а; b)) и на концах отрезка обращается в нуль f(a) = f(b) = 0, то на (a; b) найдется хотя бы одна точка c Î (a; b), в которой f'(c) = 0.
Доказательство. Так как функция f(x) непрерывна на [a; b], то по одной из теорем о непрерывных функциях она достигает на этом отрезке наибольшего значения и наименьшего. Пусть 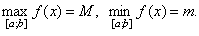
Заметим, что если М = m, то f(x) = const = 0 (по условию теоремы f(a)=f(b)=0) и, следовательно, f'(x)=0при всех x Î [a; b] .
Предположим, что M≠m, тогда, по крайней мере, одно из этих чисел отлично от нуля. Для определенности будем считать, что М ≠0 и М > 0.
Пусть в точке x = c f(c)=М, при этом c≠a и с ≠ b, т.к. f(a)=f(b)=0. Придадим значению c приращение Δx и рассмотрим новую точку c+Δx. Поскольку f(c) – наибольшее значение функции, то f(c+Δx) – f(c)≤0 для любого Δx. Отсюда следует, что
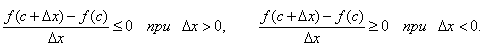
Переходя в этих неравенствах к пределу при Δx→0 и учитывая, что производная при x = c существует, будем иметь:
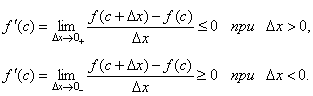
Но неравенства f'(c) ≤ 0 и f'(c) ≥ 0 одновременно возможны лишь в случае, когда
f'(c)=0. Теорема доказана.
Эта теорема имеет простой геометрический смысл. Если непрерывная кривая, имеющая в каждой точке касательную, пересекает ось Ox в точках x=a и x=b, то на этой кривой найдется хотя бы одна точка с абсциссой c, a < c < b, в которой касательная параллельна оси Ox. Заметим, что доказанная теорема останется справедливой, если предположить, что на концах отрезка функция принимает равные значения f(a)=f(b), не обязательно равные нулю. Кроме того, отметим, что если внутри [a; b] найдется хотя бы одна точка, в которой производная функции f(x) не существует, то утверждение теоремы может оказаться неверным. Пример. Функция 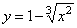 непрерывна на [–1; 1], обращается в нуль на концах отрезка. Но производная непрерывна на [–1; 1], обращается в нуль на концах отрезка. Но производная 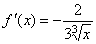 не обращается в нуль ни в одной точке этого отрезка. Теорема Лагранжа. Если функция y= f(x) непрерывна на [a; b] и дифференцируема во всех внутренних точках этого отрезка, то внутри отрезка [a; b] найдется хотя бы одна точка c, a<c<b такая, чтоf(b) – f(a)=f'(c)(b – a). Доказательство. Обозначим не обращается в нуль ни в одной точке этого отрезка. Теорема Лагранжа. Если функция y= f(x) непрерывна на [a; b] и дифференцируема во всех внутренних точках этого отрезка, то внутри отрезка [a; b] найдется хотя бы одна точка c, a<c<b такая, чтоf(b) – f(a)=f'(c)(b – a). Доказательство. Обозначим 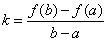 и рассмотрим вспомогательную функцию F(x) = f(x) – f(a) – k(x – a). Выясним геометрический смысл введенной функции. Для этого рассмотрим график данной функции на [a; b] и напишем уравнение хорды АВ. Заметим, что угловой коэффициент хорды и рассмотрим вспомогательную функцию F(x) = f(x) – f(a) – k(x – a). Выясним геометрический смысл введенной функции. Для этого рассмотрим график данной функции на [a; b] и напишем уравнение хорды АВ. Заметим, что угловой коэффициент хорды 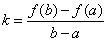 и она проходит через точку A(а; f(a)). Следовательно, ее уравнение y = f(a) + k(x – a). Но F(x)=f(x)–[f(a)+k(x–a)]. ПоэтомуF(x) при каждом x есть разность ординат графика y= f(x) и хорды, соответствующих точкам с одинаковой абсциссой. Легко видеть, что F(x) непрерывна на [a; b] , как разность непрерывных функций. Эта функция дифференцируема внутри [a; b] и F(a)=F(b)=0. Следовательно, к функции F(x) можно применить теорему Ролля. Согласно этой теореме найдется точка c Î (a; b), что F'(c)=0. Но F '(x) = f'(x) – k, а значит,F'(c) = f'(c) – k = 0. Подставляя в это равенство значение k, получим и она проходит через точку A(а; f(a)). Следовательно, ее уравнение y = f(a) + k(x – a). Но F(x)=f(x)–[f(a)+k(x–a)]. ПоэтомуF(x) при каждом x есть разность ординат графика y= f(x) и хорды, соответствующих точкам с одинаковой абсциссой. Легко видеть, что F(x) непрерывна на [a; b] , как разность непрерывных функций. Эта функция дифференцируема внутри [a; b] и F(a)=F(b)=0. Следовательно, к функции F(x) можно применить теорему Ролля. Согласно этой теореме найдется точка c Î (a; b), что F'(c)=0. Но F '(x) = f'(x) – k, а значит,F'(c) = f'(c) – k = 0. Подставляя в это равенство значение k, получим 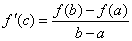 , что и требовалось доказать. , что и требовалось доказать. | 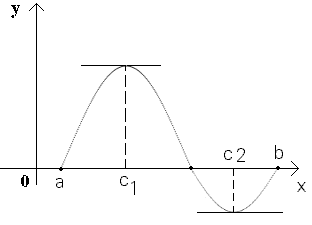 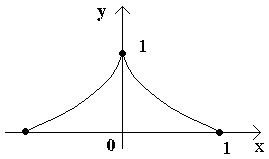 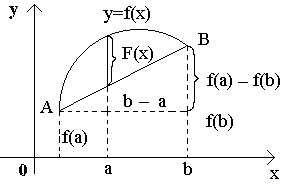 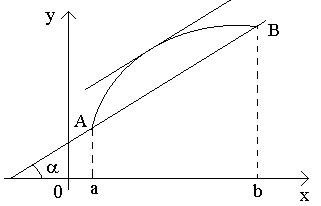 |
Теорему Лагранжа геометрически можно пояснить так. Рассмотрим график функции y=f(x), удовлетворяющий условиям теоремы и соединим концы графика на [a; b] хордой AB. Как мы уже отметили, отношение 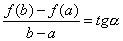 для хорды AB, а f'(c) есть угловой коэффициент касательной. Следовательно, теорема утверждает, что на графике функции y=f(x) найдется хотя бы одна точка, в которой касательная к графику параллельна хорде, соединяющей концы дуги.
для хорды AB, а f'(c) есть угловой коэффициент касательной. Следовательно, теорема утверждает, что на графике функции y=f(x) найдется хотя бы одна точка, в которой касательная к графику параллельна хорде, соединяющей концы дуги.
Теорема Коши. Если f(x) и g(x) – две функции, непрерывные на [a; b] и дифференцируемые внутри него, причем g'(x) ≠ 0 при всех x Î (a; b), то внутри отрезка [a; b] найдется хотя бы одна точка c Î (a; b), что 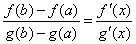 .
.
Доказательство.Определим число 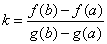 . Заметим, что g(b) – g(a) ≠ 0, т.к. в противном случае выполнялось бы равенство g(b)=g(a) и по теореме Ролля в некоторой точке d Î (a; b)g'(d) = 0. Это противоречит условию теоремы.
. Заметим, что g(b) – g(a) ≠ 0, т.к. в противном случае выполнялось бы равенство g(b)=g(a) и по теореме Ролля в некоторой точке d Î (a; b)g'(d) = 0. Это противоречит условию теоремы.
Составим вспомогательную функцию.
F(x) = f(x) – f(a) – k[g(x) – g(a)].
Несложно заметить, что F(a)=F(b)=0. Функция F(x) удовлетворяет на [a;b] всем условиям теоремы Ролля. Следовательно, найдется число сÎ(a; b) такое, что F'(c) = 0. Но
F'(x) = f'(x) – k·g(x), а значит F'(c) = f'(c) – k·g'(c) = 0,
откуда 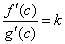 .
.
Заметим, что теорему Коши нельзя 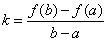
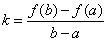 доказать, применяя теорему Лагранжа к числителю и знаменателю дроби k.
доказать, применяя теорему Лагранжа к числителю и знаменателю дроби k.
28 ВОПРОС:
Правило Бернулли[1]-Лопита́ля — метод нахождения пределов функций, раскрывающий неопределённости вида 0 / 0 и 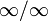 . Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.
. Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.
Условия:
1. 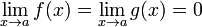 или
или 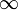 ;
;
2. 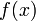 и
и 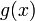 дифференцируемы в проколотой окрестности
дифференцируемы в проколотой окрестности 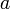 ;
;
3. 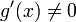 в проколотой окрестности
в проколотой окрестности 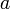 ;
;
4. существует 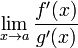 ,
,
тогда существует 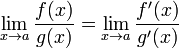 .
.
Пределы также могут быть односторонними.
29 ВОПРОС:
Выпуклые и вогнутые функции
Введем обозначение: x=(x1,x2,:,xn) - n-мерный вектор.
Определение:
n мерная функция f(x), определенная на выпуклом множестве D, называется выпуклой функцией тогда и только тогда, когда для любых двух точек x(1) и x(2) принадлежащих D, и любого числа L (0<=L<=1) выполняется неравенство:
f(Lx(1) +(1-L)x(2))<=Lf(x(1))+(1-L)f(x(2))
Проиллюстрируем определение выпуклой функции для случая одной переменной:
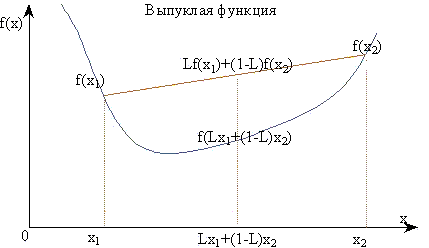
Свойства выпуклых функций:
1. Хорда, соединяющая две любые точки кривой графика выпуклой функции, всегда проходит над (или выше) кривой в интервале между двумя этими точками.
2. Выпуклая функция лежит над своими касательными
3. Тангенс угла наклона касательной, или первая производная f(x), возрастает или, по крайней мере, не убывает при увеличении x.
4. Вторая производная f(x) всегда не отрицательна на рассматриваемом интервале.
5. Для выпуклой функции локальный минимум всегда является глобальным минимумом.
Градиент функции f(x1,x2,:,xn) определяется как вектор:
С f(x1,:,xn)=(df/dx1,df/dx2,:,df/dxn)T
Матрица Гессе(гессиан) для функции f(x1,:,xn) есть симметрическая матрица порядка n*n:
Hf(x1,:,xn)=[d2f/dxidxj]=С2f
