Квадратичные формы. Приведение квадратичной формы к каноническому виду.
Важнейшей числовой характеристикой квадратной матрицы является определитель, который для матрицы An,n обозначается следующим образом:
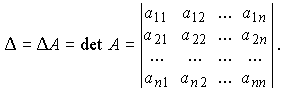
Размерность матрицы, для которой ищется определитель, задает его порядок.
Если квадратная матрица имеет определитель, отличный от нуля (Δ ≠ 0), то говорят, что матрица невырожденная, в противном случае - матрица вырожденная или особая.
Оказывается, что определитель равен сумме произведений элементов любой строки или любого столбца на соответствующие этим элементам алгебраические дополнения.
Алгебраическое дополнение элемента aij задается выражением
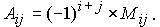
Т. е., минор Mij элемента aij берется со своим знаком, если сумма его индексов четна, и с обратным, если сумма нечетна.
Минором элемента определителя aij n-го порядка называется определитель порядка (n-1), полученный из данного определителя вычеркиванием строки и столбца, в которых находится этот элемент (i-ой строки и j-го столбца).
Рассмотрим некоторое линейное преобразование А с матрицей .
Это симметрическое преобразование можно записать в виде:
y1 = a11x1 + a12x2
y2 = a12x1 + a22x2
где у1 и у2 – координаты вектора в базисе .
Очевидно, что квадратичная форма может быть записана в виде
Ф(х1, х2) = х1у1 + х2у2.
Как видно, геометрический смысл числового значения квадратичной формы Ф в точке с координатами х1 и х2 – скалярное произведение .
Если взять другой ортонормированный базис на плоскости, то в нем квадратичная форма Ф будет выглядеть иначе, хотя ее числовое значение в каждой геометрической точке и не изменится. Если найти такой базис, в котором квадратичная форма не будет содержать координат в первой степени, а только координаты в квадрате, то квадратичную форму можно будет привести к каноническому виду.
Если в качестве базиса взять совокупность собственных векторов линейного преобразования, то в этом базисе матрица линейного преобразования имеет вид:
.
При переходе к новому базису от переменных х1 и х2 мы переходим к переменным и . Тогда:
Тогда .
Выражение называется каноническим видом квадратичной формы. Аналогично можно привести к каноническому виду квадратичную форму с большим числом переменных.
Теория квадратичных форм используется для приведения к каноническому виду уравнений кривых и поверхностей второго порядка.
Пример. Привести к каноническому виду квадратичную форму
Ф(х1, х2) = 27.
Коэффициенты: а11 = 27, а12 = 5, а22 = 3.
Составим характеристическое уравнение: ;
(27 - l)(3 - l) – 25 = 0
l2 - 30l + 56 = 0
l1 = 2; l2 = 28;
Пример. Привести к каноническому виду уравнение второго порядка:
17x2 + 12xy + 8y2 – 20 = 0.
Коэффициенты а11 = 17, а12 = 6, а22 = 8. А =
Составим характеристическое уравнение:
(17 - l)(8 - l) - 36 = 0
136 - 8l - 17l + l2 – 36 = 0
l2 - 25l + 100 = 0
l1 = 5, l2 = 20.
Итого: - каноническое уравнение эллипса.
Пределы. Теоремы пределов.
Функция 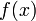 имеет предел
имеет предел 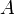 в точке
в точке 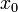 , предельной для области определения функции
, предельной для области определения функции 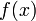 , если для каждой окрестности предела
, если для каждой окрестности предела  существует проколотая окрестность точки
существует проколотая окрестность точки 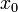 , образ которой при отображении
, образ которой при отображении 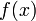 является подмножеством заданной окрестности точки
является подмножеством заданной окрестности точки 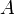 .
.
Свойства пределов числовых функций
Пусть даны функции 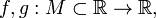 и
и 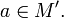 .
.
Одна и та же функция в одной и той же точке может иметь только один предел.
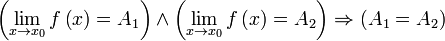
Доказательство
Сходящаяся функция локально сохраняет знак. Более обще,
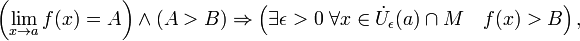
где 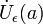 — проколотая окрестность точки a.
— проколотая окрестность точки a.
В частности, функция, сходящаяся к положительному (отрицательному) пределу, остаётся положительной (отрицательной) в некоторой окрестности предельной точки:
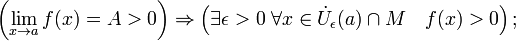
Сходящаяся функция локально ограничена в окрестности предельной точки:
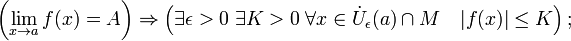
Отделимость от нуля функций, имеющих предел, отличный от нуля.
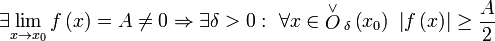
Операция взятия предела сохраняет нестрогие неравенства.
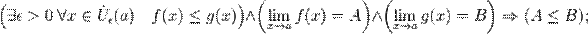
Предел суммы равен сумме пределов:
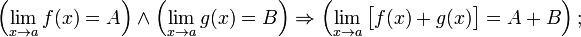
Предел разности равен разности пределов:
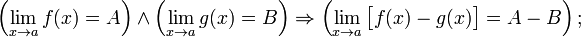
Предел произведения равен произведению пределов:
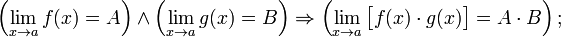
Предел частного равен частному пределов.
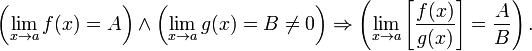
Постоянное число а называется пределом последовательности {xn}, если для любого сколь угодно малого положительного числа e существует номер N, что все значения xn, у которых n>N, удовлетворяют неравенству
|xn - a| < e. (6.1)
Записывают это следующим образом: 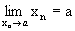 или xn→ a.
или xn→ a.
Неравенство (6.1) равносильно двойному неравенству
a- e < xn < a + e, (6.2)
которое означает, что точки x n, начиная с некоторого номера n>N, лежат внутри интервала (a-e, a+e), т.е. попадают в какую угодно малую e-окрестность точки а.
Последовательность, имеющая предел, называется сходящейся, в противном случае - расходящейся.
Понятие предел функции является обобщением понятия предел последовательности, так как предел последовательности можно рассматривать как предел функции xn = f(n) целочисленного аргумента n.
Пусть дана функция f(x) и пусть a - предельная точка области определения этой функции D(f), т.е. такая точка, любая окрестность которой содержит точки множества D(f), отличные от a. Точка a может принадлежать множеству D(f), а может и не принадлежать ему.
Замечательные пределы
Первый замечательный предел
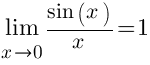 Следствия Следствия 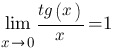 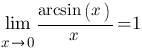 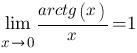 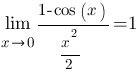 Второй замечательный предел Второй замечательный предел 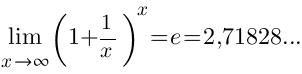 При решении примеров полезно иметь в виду следующие равенства: При решении примеров полезно иметь в виду следующие равенства: 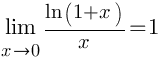 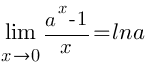 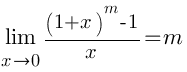 |
