Понятие вектора. Коллинеарность векторов. Их равенство.
Понятие вектора. Коллинеарность векторов. Их равенство.
Направленный отрезок или, что то же самое, упорядоченную пару точек будем называть вектором. Обозначается вектор одной буквой 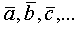 или
или 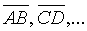 . Векторы характеризуются длиной
. Векторы характеризуются длиной 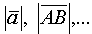 и направлением. Мы рассматриваем свободные векторы, т. е. такие, которые без изменения длины и направления могут быть перенесены в любую точку пространства.
и направлением. Мы рассматриваем свободные векторы, т. е. такие, которые без изменения длины и направления могут быть перенесены в любую точку пространства.
Ортом вектора 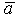 называется вектор
называется вектор 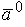 , который имеет единичную длину и то же направление, что и вектор
, который имеет единичную длину и то же направление, что и вектор 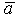 .
.
Векторы, расположенные на одной прямой или на параллельных прямых, называются коллинеарными.
Векторы, лежащие в одной плоскости или параллельные одной плоскости, называются компланарными.
Два вектора считаются равными, если они коллинеарные, одинаково направлены и равны по длине.
Пусть даны два вектора. Параллельным переносом приведем их к общему началу. Наименьший угол, на который надо повернуть один вектор до совпадения с другим, называется углом между векторами.
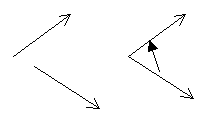
Рис.1
Координаты вектора. Разложение векторов по базису.
Три вектора , 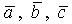 , называются линейно-независимыми, если они не лежат в одной плоскости.
, называются линейно-независимыми, если они не лежат в одной плоскости.
Базисом в трехмерном пространстве R3 называется упорядоченная тройка любых линейно-независимых векторов.
Если 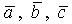 - базис в R3, то любой другой вектор, например
- базис в R3, то любой другой вектор, например 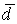 , единственным образом разлагается по этому базису
, единственным образом разлагается по этому базису
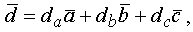
где числа da, db, dc находятся единственным образом и называются координатами вектора 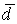 в базисе
в базисе 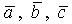
Базис 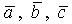 называется прямоугольным (ортогональным), если векторы
называется прямоугольным (ортогональным), если векторы 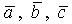 попарно перпендикулярны. Если они к тому же имеют длину, равную единице, то базис называется ортонормированным.
попарно перпендикулярны. Если они к тому же имеют длину, равную единице, то базис называется ортонормированным.
В пространстве R3 обычно используют прямоугольную декартову систему координат Оxyz, где любая точка М пространства, имеющая координаты х (абсциссу), y (ординату) и z (аппликату), обозначается М(x, y, z).
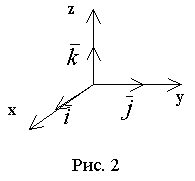
Свободный вектор, например 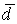 , заданный в координатном пространстве Oxyz, может быть представлен в виде
, заданный в координатном пространстве Oxyz, может быть представлен в виде
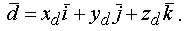
Здесь xd, yd, zd - проекции вектора 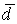 на соответствующие оси координат (координаты вектора),
на соответствующие оси координат (координаты вектора),
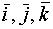 - орты этих осей.
- орты этих осей.
Пишут 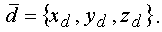
Длина вектора определяется по формуле
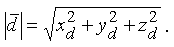
Направление вектора определяется углами α, β, γ, образованными им с осями координат Ox, Oy, Oz. Косинусы этих углов (так называемые направляющие косинусы вектора) вычисляются по формулам:
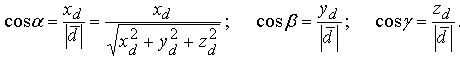
Координаты вектора будут равны
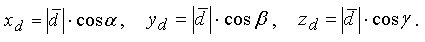
Подставив эти выражения в формулу вычисления длины вектора, установим, что направляющие косинусы вектора связаны соотношением
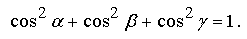
Определители. Их свойства.
Определитель первого порядка равен тому единственному элементу, из которого состоит соответствующая матрица.
Определитель второго порядка вычислим, например, по элементам первой строки
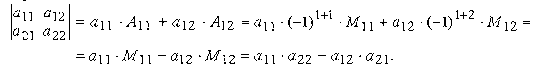
Запишем разложение данного определителя по элементам второй строки
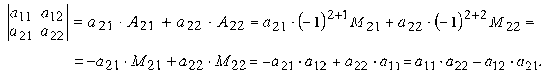
Полученный результат совпадает с результатом вычисления определителя по первой строке. Этот же результат получится и при разложении по любому из столбцов. Рекомендуем это проверить самостоятельно.
Из сказанного можно заключить, что определитель второго порядка равен произведению элементов, стоящих на главной диагонали, минус произведение элементов, стоящих на побочной диагонали.
Пример. . 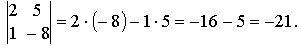
Найдем определитель третьего порядка, раскладывая его по элементам, например, третьего столбца
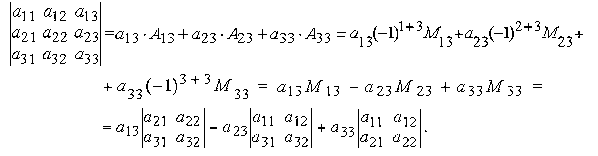
Пример.
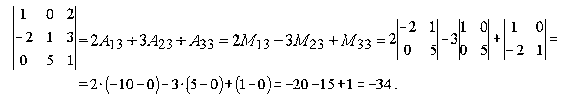
Таким образом, вычисление определителя третьего порядка сводится к вычислению определителей второго порядка.
Получается, что определитель n - го порядка мы найдем через определители (n -1) - го порядка.
Перечисленные ниже свойства рекомендуется использовать при вычислении определителей.
1. Общий множитель любой строки (столбца) можно выносить за знак определителя.
2. Если к элементам некоторой строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число, то величина определителя не изменится.
3. Если в определителе есть нулевая строка (столбец), то определитель равен нулю.
4. При перестановке двух строк (столбцов) определитель меняет знак на противоположный.
5. Определитель с двумя одинаковыми строками (столбцами) равен нулю.
Метод Крамера
Для системы n линейных уравнений с n неизвестными (над произвольным полем)
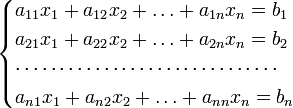
с определителем матрицы системы Δ, отличным от нуля, решение записывается в виде
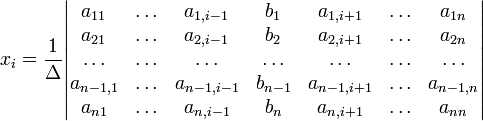
(i-ый столбец матрицы системы заменяется столбцом свободных членов).
В другой форме правило Крамера формулируется так: для любых коэффициентов c1, c2, …, cn справедливо равенство:
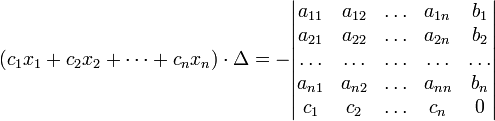
В этой форме формула Крамера справедлива без предположения, что Δ отлично от нуля, не нужно даже, чтобы коэффициенты системы были бы элементами целостного кольца(определитель системы может быть даже делителем нуля в кольце коэффициентов). Можно также считать, что либо наборы b1,b2,...,bn и x1,x2,...,xn, либо набор c1,c2,...,cn состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом. В этом виде формула Крамера используется, например, при доказательстве формулы для определителя Грама и Леммы Накаямы.
Пример
Система линейных уравнений:
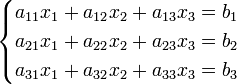
Определители:
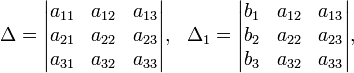
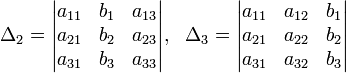
Решение:
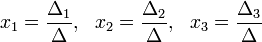
Пример:
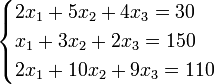
Определители:
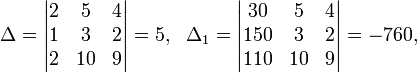
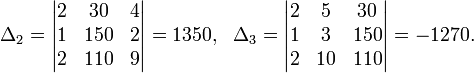
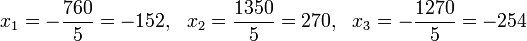
Метод Гаусса
Этот метод решения систем линейных уравнений пригоден для решения систем с любым числом уравнений и неизвестных.
Суть метода Гаусса заключается в преобразовании заданной системы уравнений с помощью элементарных преобразований в эквивалентную систему ступенчатого треугольного вида.
Полученная система содержит все неизвестные в первом уравнении. Во втором уравнении отсутствует первое неизвестное, в третьем уравнении отсутствуют первое и второе неизвестные и т. д.
Если система совместна и определена (единственное решение), то последнее уравнение содержит одно неизвестное. Найдя последнее неизвестное, из предыдущего уравнения находим еще одно - предпоследнее. Подставляя полученные величины неизвестных, мы последовательно найдем решение системы.
Элементарными преобразованиями системы линейных уравнений, используемыми для приведения системы к треугольному виду, являются следующие преобразования:
- перестановка местами двух уравнений;
- умножение обеих частей одного из уравнений на любое число, отличное от нуля;
- прибавление к обеим частям одного уравнения соответствующих частей другого уравнения, умноженных на любое число.
Элементарные преобразования переводят данную систему линейных алгебраических уравнений в эквивалентную систему.
Две системы называются эквивалентными, если всякое решение первой системы является решением другой системы и наоборот.
Пример 1. Решить систему 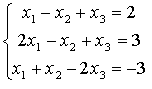 методом Гаусса.
методом Гаусса.
Решение
Определитель системы не равен нулю (см. пример из 2.2.1). Поэтому система совместна и определена (решение единственно). Выполним преобразования.
Первое уравнение оставим без изменения. Для того, чтобы избавиться от первого неизвестного во втором и третьем уравнениях, к ним прибавим первое, умноженное на -2 в первом случае и на -1 - во втором
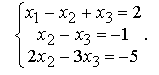
Теперь избавимся от второго неизвестного в третьем уравнении. Для этого второе уравнение умножим на -2 и прибавим к третьему. Получим эквивалентную заданной систему треугольного вида

Решаем систему снизу вверх. Из третьего уравнения имеем x3= 3 и, подставляя его во второе уравнение, находим x2= 2. Поставив найденные неизвестные в первое уравнение, получим x1= 1. Таким образом, получим решение системы: x1= 1, x2= 2, x3= 3.
Проверка: 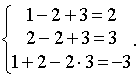 Получили три тождества.
Получили три тождества.
Пример 2. Решить систему 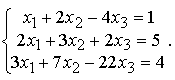
Решение
В ней 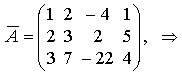 для исключения первого неизвестного во второй и третьей строках (уравнениях) умножим первую строку расширенной матрицы на -2 и -3 и сложим полученные результаты со второй и третьей строками соответственно.
для исключения первого неизвестного во второй и третьей строках (уравнениях) умножим первую строку расширенной матрицы на -2 и -3 и сложим полученные результаты со второй и третьей строками соответственно.
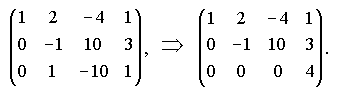
Следовательно, мы пришли к эквивалентной системе

Ее третье уравнение получено в результате сложения двух последних уравнений (строк).
Найдя 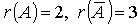 , мы приходим к выводу, что система несовместна. Об этом же говорит и противоречие в третьем уравнении системы.
, мы приходим к выводу, что система несовместна. Об этом же говорит и противоречие в третьем уравнении системы.
Пример 2. Решить систему 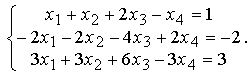
Решение
В ней 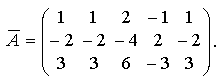
Умножим первую строку расширенной матрицы на 2 и -3, сложим полученные результаты со второй и третьей строками соответственно и получим
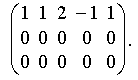
Следовательно, мы пришли к эквивалентной системе
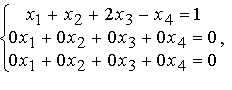
которая может быть представлена в виде
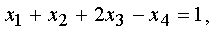
поскольку два последних уравнения - истинные равенства.
Поскольку 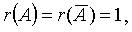 постольку система совместна, но имеет множество решений. Общее решение системы имеет вид
постольку система совместна, но имеет множество решений. Общее решение системы имеет вид
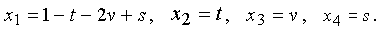
Множество частных решений системы будет трехмерным, так как зависит от трех параметров. Выбрав t = 2, v = 1, s = -3, получим частное решение системы x1 = - 6, x2 = 2, x3 = 1, x4= -3.
Матричный метод
Матричным методом могут быть решены только те системы, у которых число уравнений совпадает с числом неизвестных и определитель матрицы коэффициентов отличен от нуля (матрица А невырожденная).
Из этих условий следует, что 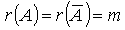 и, следовательно, система совместна и определена.
и, следовательно, система совместна и определена.
Решение системы можно получить так: 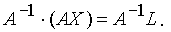
Используя свойства произведения матриц и свойство обратной матрицы
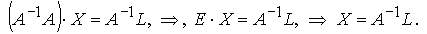
Т.е., для получения столбца неизвестных нужно обратную матрицу матрицы коэффициентов системы умножить на столбец свободных членов.
Пример Решить систему 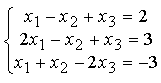 матричным методом.
матричным методом.
Решение
В соответствии с пунктом 1.5 найдем обратную матрицу для матрицы коэффициентов системы
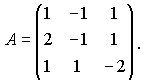
Вычислим определитель, раскладывая по первой строке:
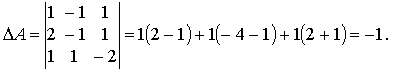
Поскольку Δ ≠ 0, то A-1 существует.

Обратная матрица найдена верно.
Найдем решение системы 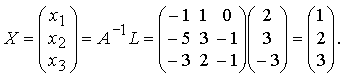
Следовательно, x1 = 1, x2 = 2, x3 = 3.
Проверка: 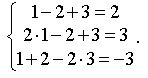
Система решена верно.
Матричный метод годится для решения любых систем, у которых матрица А квадратная и невырожденная.
Собственные значения
У матрицы A , размерностью (N×N) не может быть больше чем N собственных значений. Они удовлетворяют характеристическому уравнению
det(A − λI) = 0,
являющемуся алгебраическим уравнением N-го порядка. В частности, для матрицы 2×2 характеристическое уравнение имеет вид
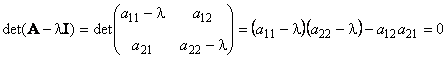
Например,

Рис. 21 Собственные значения
Набор собственных значений λ1,..., λN матрицы A называется спектром A.
Спектр обладает разнообразными свойствами. В частности
det(A) = λ1×...×λN, Sp(A) = λ1+...+λN.
Собственные значения произвольной матрицы могут быть комплексными числами, однако если матрица симметричная (At = A), то ее собственные значения вещественны.
Собственные векторы
У матрицы A, размерностью (N×N) не может быть больше чем N собственных векторов, каждый из которых соответствует своему собственному значению. Для определения собственного вектора vn нужно решить систему однородных уравнений
(A − λnI) vn = 0.
Она имеет нетривиальное решение, поскольку det(A − λnI) = 0.
Например,

Рис. 22 Собственные вектора
Собственные вектора симметричной матрицы ортогональны.
Пределы. Теоремы пределов.
Функция 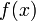 имеет предел
имеет предел 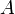 в точке
в точке 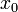 , предельной для области определения функции
, предельной для области определения функции 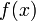 , если для каждой окрестности предела
, если для каждой окрестности предела 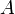 существует проколотая окрестность точки
существует проколотая окрестность точки 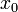 , образ которой при отображении
, образ которой при отображении 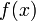 является подмножеством заданной окрестности точки
является подмножеством заданной окрестности точки 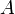 .
.
Свойства пределов числовых функций
Пусть даны функции 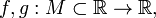 и
и 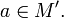 .
.
Одна и та же функция в одной и той же точке может иметь только один предел.
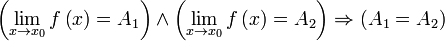
Доказательство
Сходящаяся функция локально сохраняет знак. Более обще,
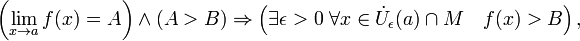
где 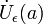 — проколотая окрестность точки a.
— проколотая окрестность точки a.
В частности, функция, сходящаяся к положительному (отрицательному) пределу, остаётся положительной (отрицательной) в некоторой окрестности предельной точки:
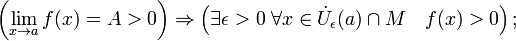
Сходящаяся функция локально ограничена в окрестности предельной точки:
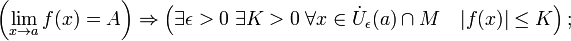
Отделимость от нуля функций, имеющих предел, отличный от нуля.
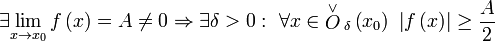
Операция взятия предела сохраняет нестрогие неравенства.
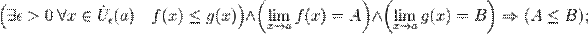
Предел суммы равен сумме пределов:
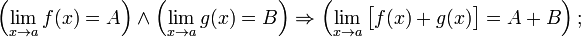
Предел разности равен разности пределов:
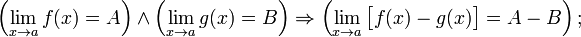
Предел произведения равен произведению пределов:
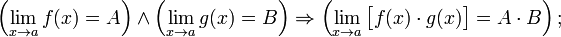
Предел частного равен частному пределов.
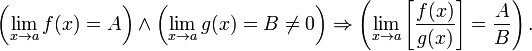
Постоянное число а называется пределом последовательности {xn}, если для любого сколь угодно малого положительного числа e существует номер N, что все значения xn, у которых n>N, удовлетворяют неравенству
|xn - a| < e. (6.1)
Записывают это следующим образом: 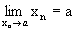 или xn→ a.
или xn→ a.
Неравенство (6.1) равносильно двойному неравенству
a- e < xn < a + e, (6.2)
которое означает, что точки x n, начиная с некоторого номера n>N, лежат внутри интервала (a-e, a+e), т.е. попадают в какую угодно малую e-окрестность точки а.
Последовательность, имеющая предел, называется сходящейся, в противном случае - расходящейся.
Понятие предел функции является обобщением понятия предел последовательности, так как предел последовательности можно рассматривать как предел функции xn = f(n) целочисленного аргумента n.
Пусть дана функция f(x) и пусть a - предельная точка области определения этой функции D(f), т.е. такая точка, любая окрестность которой содержит точки множества D(f), отличные от a. Точка a может принадлежать множеству D(f), а может и не принадлежать ему.
Замечательные пределы
Первый замечательный предел
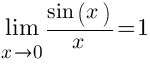 Следствия Следствия 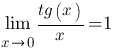 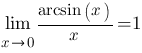 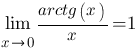 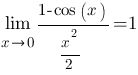 Второй замечательный предел Второй замечательный предел 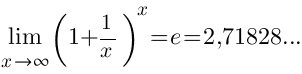 При решении примеров полезно иметь в виду следующие равенства: При решении примеров полезно иметь в виду следующие равенства: 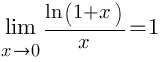 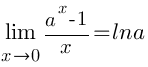 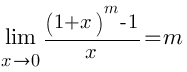 |
Понятие вектора. Коллинеарность векторов. Их равенство.
Направленный отрезок или, что то же самое, упорядоченную пару точек будем называть вектором. Обозначается вектор одной буквой 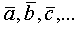 или
или 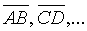 . Векторы характеризуются длиной
. Векторы характеризуются длиной 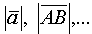 и направлением. Мы рассматриваем свободные векторы, т. е. такие, которые без изменения длины и направления могут быть перенесены в любую точку пространства.
и направлением. Мы рассматриваем свободные векторы, т. е. такие, которые без изменения длины и направления могут быть перенесены в любую точку пространства.
Ортом вектора 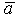 называется вектор
называется вектор 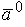 , который имеет единичную длину и то же направление, что и вектор
, который имеет единичную длину и то же направление, что и вектор 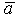 .
.
Векторы, расположенные на одной прямой или на параллельных прямых, называются коллинеарными.
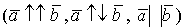
Векторы, лежащие в одной плоскости или параллельные одной плоскости, называются компланарными.
Два вектора считаются равными, если они коллинеарные, одинаково направлены и равны по длине.
Пусть даны два вектора. Параллельным переносом приведем их к общему началу. Наименьший угол, на который надо повернуть один вектор до совпадения с другим, называется углом между векторами.

Рис.1
