Какие матрицы можно умножать?

Чтобы матрицу 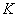можно было умножить на матрицу 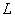нужно, чтобы число столбцов матрицы 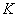равнялось числу строк матрицы .

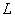Пример:
Можно ли умножить матрицу 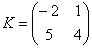на матрицу ?

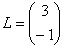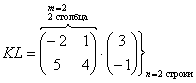
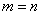, значит, умножать данные матрицы можно.

А вот если матрицы переставить местами, то, в данном случае, умножение уже невозможно!

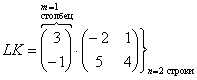
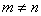, следовательно, выполнить умножение невозможно:

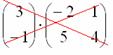
Не так уж редко встречаются задания с подвохом, когда студенту предлагается умножить матрицы, умножение которых заведомо невозможно.

Следует отметить, что в ряде случаев можно умножать матрицы и так, и так.
Например, для матриц, 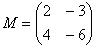и 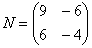возможно как умножение 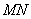, так и умножение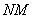

Как умножить матрицы?

Умножение матриц лучше объяснить на конкретных примерах, так как строгое определение введет в замешательство (или помешательство) большинство читателей.

Начнем с самого простого:

Пример:

Умножить матрицу 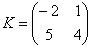на матрицу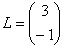
Я буду сразу приводить формулу для каждого случая:

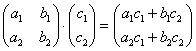– попытайтесь сразу уловить закономерность.

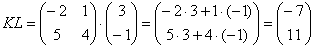
Пример сложнее:

Умножить матрицу 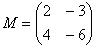на матрицу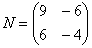

Формула: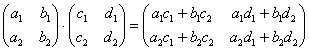

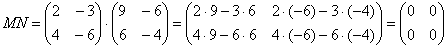
В результате получена так называемая нулевая матрица.

Попробуйте самостоятельно выполнить умножение 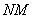(правильный ответ ).

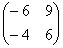Обратите внимание, что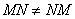 ! Это почти всегда так!

Таким образом, при умножении переставлять матрицы нельзя!

Если в задании предложено умножить матрицу 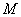на матрицу 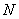, то и умножать нужно именно в таком порядке. Ни в коем случае не наоборот.

Вопрос преобразований. 8Нахождение обратной матрицы с помощью элементарных преоразований

Как найти обратную матрицу методом Гаусса?

Обычно условие формулируют сокращённо, но, по существу, здесь также работает алгоритм Жордано-Гаусса. Краткое содержание предстоящих действий таково: сначала следует записать квадратную матрицу 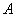в тандеме с единичной матрицей: 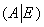. Затем с помощью элементарных преобразований необходимо получить единичную матрицу слева, при этом (не вдаваясь в теоретические подробности) справа нарисуется обратная матрица. Схематически решение выглядит следующим образом:

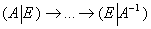
(Понятно, что обратная матрица должна существовать)

Демо-пример: найдём обратную матрицу для матрицы 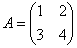с помощью элементарных преобразований. Для этого запишем её в одной упряжке с единичной матрицей: .

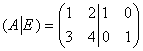Так вот, в рассматриваемой задаче КАТЕГОРИЧЕСКИ ЗАПРЕЩЕНО переставлять строки.

Однако не всё так плохо:

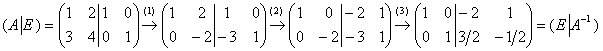
(1) Ко второй строке прибавили первую строку, умноженную на –3.

(2) К первой строке прибавили вторую строку.

(3) Вторую строку разделили на –2.

Таким образом: .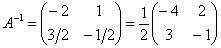

Вопрос 9. Линейная зависимость строк или столбцов в матрице.

Понятия линейной зависимости и линейной независимости определяются для строк и столбцов одинаково. Поэтому свойства, связанные с этими понятиями, сформулированные для столбцов, разумеется, справедливы и для строк.