Тема 5. Дифференциальное исчисление
Занятие 1
1. Повторение определений основных понятий темы.
2. Решить задачи [Л1, с. 350 – 355]:
7.20(б, г); 7.33; 7.34; 7.42 на дом 7.27; 7.39; 7.55; 7.61; 7.62.
3. Найти первую и вторую производные функций:
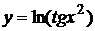 на дом
на дом 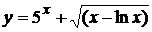
4. Решить задачи [Л1, с.355]:
7.64 на дом 7.65; 7.66.
5. Написать уравнение касательной и нормали к графику функции 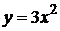 в заданной точке
в заданной точке 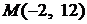 .
.
6. Решить задачи [Л1, с.359]:
7.110 на дом 7.108; 7.112.
Занятие 2
1. Повторение определений основных понятий темы.
2. Решить задачи [Л1, с.356]:
7.76, 7.78, 7.80 на дом 7.77, 7.81.
3. Исследовать функции и построить их графики
а) 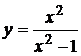 ; б)
; б) 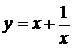
на дом а) 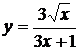 ; б)
; б) 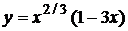 .
.
4. Решить задачи [Л1, с.361]:
7.125; 7.130 на дом 7.126; 7.127; 7.131; 7.133.
Тема 6. Неопределенный и определенный интегралы
Занятие 1
1. Повторение определений основных понятий темы.
2. Найти неопределенные интегралы методом непосредственного интегрирования
а) 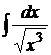 ; б)
; б) 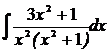 ; в)
; в) 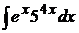 .
.
Решить задачи [Л1, с.548 – 549]:
10.34 на дом 10.25; 10.32, 10.36.
3. Найти неопределенные интегралы методом замены переменной
а) 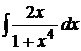 ; б)
; б) 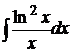 ; в)
; в) 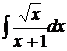 .
.
Решить задачи [Л1, с. 549, 554 – 556]:
10.41(в); 10.48 на дом 10.43; 10.46; 10.55; 10.76; 10.80; 10.90.
4. Найти неопределенные интегралы методом интегрирования по частям.
Решить задачи [Л1, с. 556, 560]:
10.95(а); 10.97; 10.100; 10.104
на дом 10.107; 10.118, 10.125, 10.126.
Занятие 2
1. Повторение определений основных понятий темы.
2. Найти неопределенные интегралы от рациональных дробей
Решить задачи [Л1, с.565]:
10.127; 10.128; на дом 10.137; 10.140, 10.144, 10.150.
3. Вычислить определенные интегралы
Решить задачи [Л1, с.621]:
11.32, 11.37, 11.50 на дом 11.40, 11.43
4. Найти площади фигур, ограниченных следующими кривыми
а) 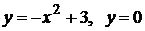 ; б)
; б) 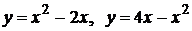
на дом а) 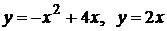 ; б)
; б) 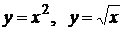 .
.
Решить задачи [Л1, с.630]:
11.65 на дом 11.64; 11.72; 11.73; 11.84.
5. Вычислить несобственные интегралы
а) 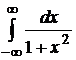 ; б)
; б) 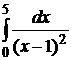 .
.
Решить задачи [Л1, с.635 - 636]:
11.115; 11.118; 11.123 на дом 11.124; 11.128; 11.129; 11.133.
Тема 7. Ряды
Занятие 1
1. Повторение определений основных понятий темы.
2. Доказать непосредственно сходимость рядов и найти их суммы
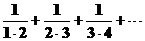 на дом
на дом 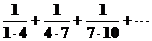 .
.
Решить задачи [Л1, с.741]:
13.19 на дом 13.20; 13.22.
3. Исследовать сходимость знакопостоянного числового ряда
а) 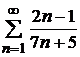 ; б)
; б) 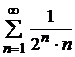 ; в)
; в) 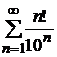 ;
;
на дом а) 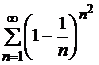 ; б)
; б) 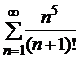 ; в)
; в) 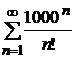 .
.
Решить задачи [Л1, с.748 – 750]:
13.38; 13.61; 13.64; 13.84
на дом 13.67, 13.71; 13.90 – 13.92.
4. Исследовать сходимость знакочередующегося числового ряда
а) 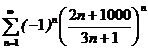 ; б)
; б) 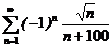 ;
;
Решить задачи [Л1, с.753, 754]:
13.106, 13.113 на дом 13.120, 13.123.
Занятие 2
1. Повторение определений основных понятий темы.
2. Найти область сходимости степенного ряда
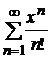 .
.
Решить задачи [Л1, с.776]:
14.11; 14.15; 14.21 на дом 14.14; 14.20; 14.21; 14.23; 14.27.
3. Разложить функции в ряд Маклорена и найти радиус сходимости ряда
а) 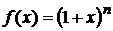 ; б)
; б) 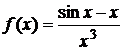 .
.
4. Решить задачи [Л1, с.783]:
14.41, 14.43, на дом 14.45; 14.52; 14.66.
Тема 8. Функции нескольких переменных
Занятие 1
1. Повторение определений основных понятий темы.
2. Найти частные производные функций двух переменных
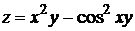 .
.
Решить задачи [Л1, с.504, 505]:
9.44, 9.46, на дом 9.47; 9.50; 9.51; 9.53.
3. Полагая, что произвольная функция 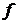 дифференцируема, проверить следующие равенства:
дифференцируема, проверить следующие равенства:
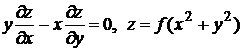
на дом 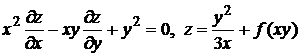 .
.
4. Решить задачи [Л1, с.505]:
9.64 на дом 9.66; 9.68.
Найти величину и направление градиента функции в точке 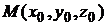 :
:
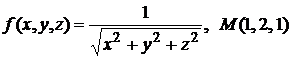 ;
;
на дом 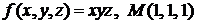 .
.
Занятие 2
1. Повторение определений основных понятий темы.
2. Решить задачи [Л1, с.509]:
9.75; 9.88 на дом 9.76; 9.81; 9.84.
Найти точки локального экстремума функций и проверить в них выполнение достаточного условия экстремума
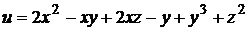 .
.
3. Вычислить двойные интегралы 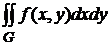 по области
по области 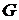 , заданной границами
, заданной границами
а) 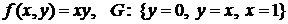 ;
;
б) 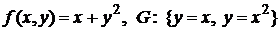
на дом 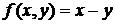 ,
, 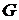 – треугольник с вершинами (1, 1), (4, 1), (4, 4).
– треугольник с вершинами (1, 1), (4, 1), (4, 4).
Решить задачи [Л1, с.643, 644]:
11.159 11.160.
4. С помощью двойного интеграла найти площадь, ограниченную следующими кривыми:
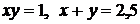 ; на дом
; на дом 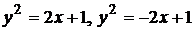 .
.
Тема 9. Случайные события
Занятие 1.
1. Повторение определений основных понятий темы.
2. Решить задачи [Л6[3], с.34 – 37]:
1.17а; 1.18; 1.19.
3. Среди 25 студентов, из которых 15 девушек, разыгрываются 4 приглашения на дискотеку, причем каждый может выиграть только один билет. Какова вероятность того, что среди обладателей билета окажутся а) только девушки, б) только юноши?
На дом
Какова вероятность того, что среди обладателей билета окажутся
две девушки и двое юношей?
4. Решить задачи [Л6, с.61 – 62]:
1.37; 1.43; 1.45 на дом 1.38; 1.45; 1.51.
5. В одной группе Г1 студентов, из которых О1 учатся на «отлично». В другой – Г2 студентов, из которых на «отлично» учатся О2. Из каждой группы случайным образом выбрали по одному студенту. Какова вероятность того, что оба учатся на «отлично»?
а) Г1=18; О1=9; Г2=16; О2=4
На дом
б) Г1=15; О1=5; Г2=20; О2=6.
6. Решить задачи [Л6, с.45, 63]:
1.26а-б; 1.55 на дом 1.26в-д; 1.56.
Занятие 2.
1. Повторение определений основных понятий темы.
2. В семье двое детей. Известно, что один из них мальчик. Какова вероятность, что оба ребенка – мальчики?
3. По результатам проверки зачетных работ оказалось, что в первой группе получили зачет 20 студентов из 30, а во второй 16 из 32. Какова вероятность того, что наудачу выбранная зачтенная работа принадлежит студенту первой группы?
4. Решить задачи [Л6, с.49-50, 63-65]:
1.31а; 1.65; 1.68; 1.69 на дом 1.33а; 1.70; 1.82.
5.Два стрелка сделали по одному выстрелу в одну и ту же мишень. Вероятность попадания в мишень для первого стрелка равна 0,6, а для второго – 0,4. В мишени оказалась одна пробоина. Найти вероятность того, что пробоина принадлежит первому стрелку.
На дом
Два стрелка сделали по одному выстрелу в одну и ту же мишень. Вероятность попадания в мишень для первого стрелка равна 0,8, а для второго – 0,5. В мишени оказалась одна пробоина. Найти вероятность того, что пробоина принадлежит второму стрелку.
Занятие 3
1. Повторение определений основных понятий темы.
2. Решить задачи [Л6, с. 53, 64-67]:
1.34; 1.72; 1.78; 1, 85; 1.98 на дом 1.73; 1.75; 1.87; 1.95; 1.97.
3. Вероятность, что малое предприятие станет банкротом в течение года равна 0,2. Найти вероятность, что из восьми малых предприятий за первый год обанкротятся два предприятия.
На дом
Найти вероятность, что из восьми малых предприятий за первый год обанкротятся более двух предприятий.
Тема 2. Случайные величины
Занятие 1
1. Повторение определений основных понятий темы.
2. Решить задачи [Л6, с.90-92]:
3.2; 3.3.
Построить функцию распределения, найти математическое ожидание, дисперсию и среднеквадратическое отклонение исходных и полученных случайных величин.
3. Решить задачи [Л6, с.133-137]:
3.25; 3.28; 3.31; 3.52 на дом 3.26; 3.29; 3.34; 3.54.
Занятие 2
1. Повторение определений основных понятий темы.
2. Клиенты банка, не связанные друг с другом, не возвращают кредиты в срок с вероятностью 0,1. Составить закон распределения числа возвращенных в срок кредитов из числа выданных. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение числа возвращенных кредитов.
3. Случайные величины X и Y независимы и имеют один и тот же закон распределения.
| Значение | |||
| Вероятность | 0,2 | 0,3 | 0,5 |
Составить закон распределения случайных величин Z=2X и W=X+Y. Найти их математическое ожидание, дисперсию и среднее квадратическое отклонение.
4. Решить задачи [Л6, с.135-140]:
3.36; 3.41; 3.49; 3.58 на дом 3.43; 3.50; 3.57; 3.59; 3.64; 3.72.
