Точка разрыва является точкой разрыва 1-ого рода, если оба односторонние пределы в этой точке существуют, являются конечными числами, не равными между собой.

Точка разрыва является точкой разрыва 2-ого рода, если хотя бы один из односторонних пределов не существует или равен бесконечности.

Точка разрыва называется устранимой, если оба односторонних предела существуют, являются конечными числами, равными между собой, но не равны значению функции в этой точке.

27. Теоремы о непрерывных функциях

1)Первая теорема Вейерштрасса

Если ф-ция f(x) непрерывна на отрезке [а, b], то она ограничена на этом отрезке.

Теорема неверна, если в ней отрезок заменить интервалом (а,b) или полуинтервалом[a,b) либо (a,b]

2) Вторая теорема Вейерштрасса

Если ф-ция f(x)прерывна на отрезке [a, b], то она достигает на этом отрезке своего наименьшего значения m и наиб. Значения М, т.е. сущ-ют точки , 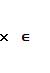[a, b], такие, что f( 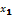)=m, f(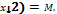

Теорема утверж-т, что знач-я непрерыв.на отрезке [а, b] ф-ции заключены между ее наибольшими и наимен. знач-ями, т.е. m ≤ f(x) ≤M 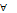x

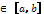
Теорема Больцано-Коши о промежут.значении

Если ф-ция f(x) непрерывна на отрезке [a, b]и f(a)=A, f(b)=B (A≠B), то каково бы ни было число С, заключенное между А и В, найдется точка z 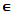[a, b], такая, что f(z)=C.

Cледствие. Если ф-ция f(x) непрерывна на отрезке [a, b] и на его концах принимает знач-я разных знаков, то на этом отрезке сущ-ет хотя бы одна точка 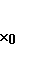, в кот. ф-ция обращается в нуль, т.е.f( 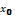)=0

Алгебраич.сумма любого конечного числа непрерыв. на некот. отрезке ф-ций непрерывна на этом отрезке.

28.Произв. ф-ции. Геометр., механ., экон. смысл произ-ной. Эласт-сть ф-ции, ее экон приложение.

Пусть ф-ция y=f(x) определена на некот множ-тве Х, тогда произв.ф-цией y=f(x) назыв. предел отношения приращения ф-ции к приращению независ. переменной, если этот предел сущ-ет когда приращ-е аргумента стремится к нулю. Если ввести обозначения: то выраж-е можно записать в виде:

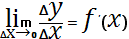Обозначается произ-я у’, f’(x), ,

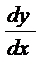C геометр. точки зр. значения производной ф-ции, вычисленное в некот. точке численно равно угловому коофициенту касательной, проведенной к графику ф-ции у=f(x) в точке с абсциссой ,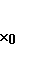

Т.е. f’(

F’(

Пусть задана ф-ция S=S(t), кот. опред-ет зависимость пути от времени,в механике S’(t)=V –мгнов.скорость в момент времени t.

Пусть задана ф-ция у=f(x), для которой сущ-ет производная у’=f’(x). Эластич-тью ф-ции у=f(x) относ-но переменной х назыв-ся предел:

Его обознач-т

Эластич-ть относ-но х есть приближен.процентн прирост ф-ции (повышение/пониж-е) при приращении независ переменной на 1%.

29.Производная показательной неявной функции.Производные высших порядков:

Производная показательной функции:

При 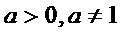для любого х

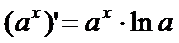
Производная неявной функции:

При вычислении производной неявной функции воспользуемся правилом дифференцирования сложной функции. Продифференцируем уравнение 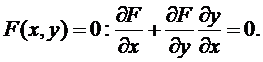. Отсюда получим формулу для производной функции 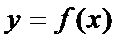, заданной неявно: 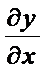= 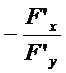. Таким же способом нетрудно получить формулы для частных производных функции нескольких переменных, заданной неявно, например, уравнением :

, .

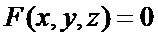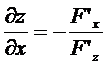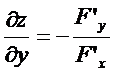Производные высших порядков:

Если f '(x) — производная функции f (x), то производная от нее по независимой переменной x, (f '(x))' = f ''(x), называется производной второго порядка. Аналогично определены производные 3-го, 4-го, , и т.д, n-го порядка: f''' (x) = ( f'' (x))' , f (4)(x) = (f''' (x))' , f (n)(x) = (f (n -1)(x))'

30. Теорема Лагранжа. Правило Лопиталя.

Теорема Лагранжа: Пусть задана ф-я 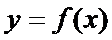и пусть она: 1) опр-на и непрер на 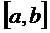; 2) имеет кон произв-ю 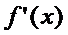на 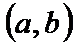. Тогда найдётся такая т. с (a<c<b), что вып-ся рав-во

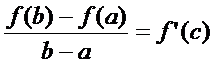Док-во: Введём вспомогат функцию

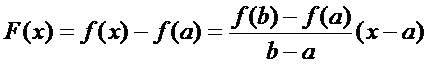
Она удовл-т всем условиям теоремы Ролля. Действительно, F(x) опред-на и непрер на , ,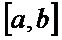

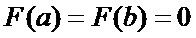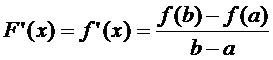,т.е. сущ на 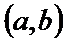. След-но, найдётся точка с (a<c<b), такая, что F’(c) = 0, т.е.

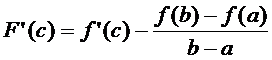или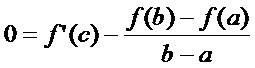

Тогда ∆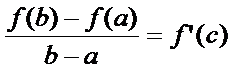

Правило Лопиталя: Пусть ф-и f(x) и g(x) одновр явл либо бескон б-ми, либо беск-но малыми в т. 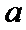. Тогда при выч-и пределов 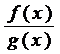при x → 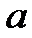для раскрытия неопред-тей вида или 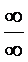удобно применить пр. Лопиталя :

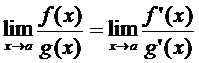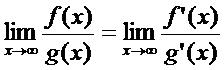, Неопределенности вида 0 · ∞, ∞ – ∞, 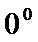, , 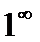часто удается свести к неопределенностям вида 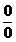или с помощью различных преобразований.

31. Достаточное усл-е возраст-я (убыв-я) ф-й.

Ф-я 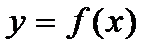наз-сявозраст-ейна инт-ле 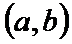, если для любых 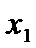и 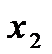из этого инт-ла, для которых 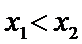, верно нерав-во 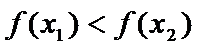.Ф-я 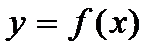наз-сяубыв-ей на инт-ле 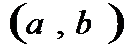, если для любых x₁ и x₂ из этого инт-ла, для кот 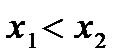, верно нерав-во 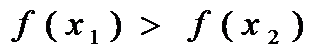.Необх-ое усл-е возраст-я ф-ии:если ф-ия 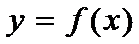диффер-ма и возраста на инт-ле 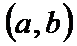, то 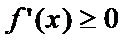для всех х из этого инт-ла.Необх-ое усл-е убыв-я ф-ции.Если ф-ция 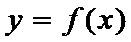дифф-ма и убыва на инт-ле 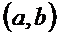, то 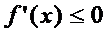для всех х из этого инт-ла.Достаточное усл-е возраст-я (убыв-я ф-и).Пусть ф-я 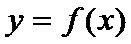диф-ма на инт-ле 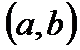. Если во всех точках этого инт-ла 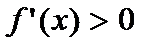, то ф-ия возраста на этом интле, а если 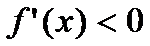, то ф-я убывает на этом инт-ле.

32. Экстремумы ф-й.

Точка x = x0 называется точкой максимума, а число 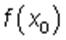— максимумом функции, если для всех точек из некоторой окрестности точки x0 , не совпадающих с x0 , выполняется неравенство .

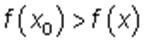Точка x = x0 называется точкой минимума, а число 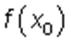— минимумом функции, если для всех точек из некоторой окрестности точки x0 , не совпадающих с точкой x0 , выполняется неравенство .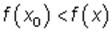