Нормалью кривой называется прямая перепенлик касательной, проведенной к графику данной функции в данной точке.

Определенный интеграл и его геометрический смысл, свойства

26.1Определенным интегралом от функции f(x) на отрезке ab называется число равное пределу n-ой интегральной суммы когда наибольшее из частичных отрезков разбиения стремится к нулю, при n стремящейся к бесконечности:

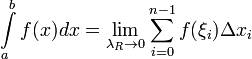
26.2

Определённый интеграл 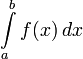численно равен площади фигуры, ограниченной осью абсцисс, прямыми и и 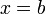графиком функции .

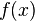Формулы Ньютона-Лейбница. Правило вычисления определенного интеграла

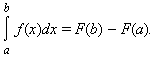
Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f, вычислить ее значения в точках a и b и найти разность F (b) – F (a).

Метод замены переменной в определенном интеграле

Пусть:

1) f(x) определена и непрерывна на [a, b];

2) x = g(t) определена и непрерывна вместе с производной

на [a, b], где g(a) = a, g(b) = b

и a ≤ g(t) ≤ b.

Тогда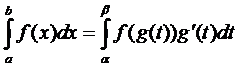

Метод интегрирования по частям в определенном интеграле

Если u(x) и v(x) имеют непрерывные производные на [a, b], то

,

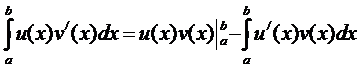или

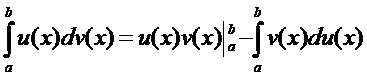
Св-ва определенного интеграла для четной и нечетной функции на симметричном промежутке

Если функция 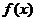интегрируема на промежутке ,

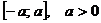то для чётной функции ,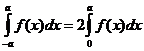

а для нечётной функции .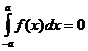

Геометрическое приложения определенного интеграла. Вычисление площадей плоских фигур

1. Пусть функция 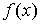непрерывна и неотрицательна на отрезке [a, b]. Тогда площадь фигуры, ограниченной осью ОХ, отрезками прямых x = a, x = b и графиком функции 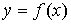, может быть вычислена по формуле 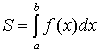(см. 10.1 рис. 1).

2. Если 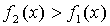на отрезке [a, b], 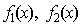- непрерывные функции, то площадь фигуры, ограниченной прямыми х = а, x = b, графиками функций 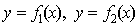вычисляется по формуле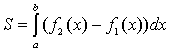

3. Если функция 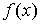на отрезке [a, b] принимает значения разных знаков, то площадь фигуры, заключенная между кривой 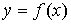и осью 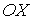, равна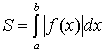

Пусть функция f (х) непрерывна на отрезке [a ; b].
Если при этом f (х) ≥ 0 на [a ; b], то площадь S криволинейной трапеции, ограниченной линиями
,
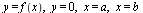выразится с помощью интеграла: 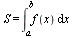(1)

Если же f (х) ≤ 0 на [a ; b], то −f (х) ≥ 0 на [a ; b].
Поэтому площадь S соответствующей криволинейной трапеции находится по формуле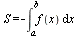
или
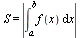(2)

Наконец, если линия у = f (х) пересекает ось Ох, то отрезок [a ; b] надо разбить на части, в пределах которых f (х) не меняет знака, и к каждой части применить ту из формул (1) или (2), которая ей соответствует

Задачи, приводящие к дифференциальным уравнениям. Определение дифференциального уравнения, его свойства.

Дифференциальные уравнения связывают между собой неизвестную функцию (или несколько таких функций) с её производными.

Дифференциальными уравнениями называются такие уравнения, в которых неизвестной величиной является функция одной или нескольких аргументов и входит в уравнение под знаком производной, а также без знака производной.

1.

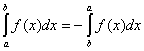
2.

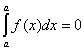
3.

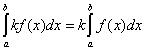
4.

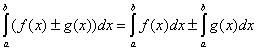
5.

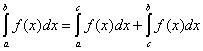
Виды событий. Примеры.

Достоверным событием называют событие которое обязательно произойдет в результате данного испытания ( восход солнца).

Событие которое никогда не произойдет при данном испытании называется невозможным.

Случайными событиями будут называться события которые могут произойти , а могут и не произойти при данном испытании

Совместными называются события если появление одного из них не исключает появление другого.

Два события называются несовместными если появление одного из них исключает появление другого.

Полной группой случайных событий называются события состоящие в появлении хотя бы одного из этих событий.

Два события называют противоположными если они не совместимы и образуют полную группу.

Равновозможными называются события если они имеют одинаковые шансы их появления.

Благоприятствующими исходами испытания называются исходы испытания при которых появляется случайное событие А.

Статической вероятностью w(A) или относительной частотой называют отношение числа благоприятных данному событию исходов к общему числу фактически проведенных испытаний.

w(A)=nm

Относительная частота события обладает свойством устойчивости:limn→∞P(∣ ∣ nm−p∣ ∣ <ε)=1 (свойство устойчивости относительной частоты)

Формула Бернулли.

Закон распределения Бернулли. Случайная величина 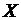, распределенная по закону Бернулли (индикаторная случайная величина), принимает значения: 1 – «успех» или 0 – «неудача» с вероятностям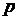и и 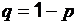соответственно

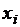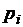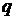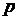Математическое ожидание случайной величины : .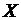

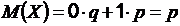Дисперсия: .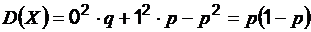

Законом распределения дискретной случайной величины называется соотношение между ее возможными значениями и их вероятностями (т. е. вероятностями, с которыми случайная величина принимает эти возможные значения).

Функцией распределения (интегральной функцией распределения) случайной величины 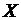называется функция

,

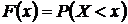определяющая вероятность того, что случайная величина 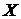примет значение, меньшее .

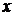Свойства функции распределения:

а) функция распределения принимает значения только из отрезка [0,1]:

0 ≤ F(x) ≤ 1;

б) F(x) – неубывающая функция, т.е. если x₂ > x₁, то F(x₂) > F(x₁) ;

в) F(- ∞ ) = 0; F(+ ∞) = 1;

г) вероятность того, что случайная величина примет значение из

интервала 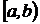(причем 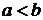), равна:

;

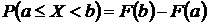д) F(x) непрерывна слева, т. е. F(x) = F(x – 0)

Закон распределения дискретной случайной величины может быть представлен в виде многоугольника распределения – фигуры, состоящей из точек 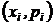, соединенных отрезками

Нормалью кривой называется прямая перепенлик касательной, проведенной к графику данной функции в данной точке.

y−f(x0)=f/(x0)(x−x0) , или

y=f/(x0)·x+f(x0)−f/(x0)·x0.

10. Правила и формулы дифференцирования

Если с - постоянное число, и u = u(x), v = v(x) - некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:

1) (с) ' = 0, (cu) ' = cu';

2) (u+v)' = u'+v';

3) ( uv )' = u'v+v'u;

4) (u/v)' = (u'v-v'u)/v ^2;

5) если y = f(u), u = j (x), т.е. y = f( j (x)) - сложная функция, или суперпозиция, составленная из дифференцируемых функций j и f, то 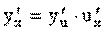, или

;

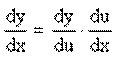6) если для функции y = f(x) существует обратная дифференцируемая функция x = g(y), причем 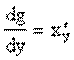¹ 0, то .

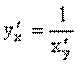11. Производная сложной функции.

ﾏроизводная сложной функции по независимой переменной равна произведению производной функции по промежуточной переменной на произведение промежуточной переменной по независимой.

12. Производная неявно заданной функции.

Чтобы найти производную неявно заданной функции, необходимо продифференцировать обе части равенства 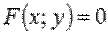по аргументу x, считая y – функцией от x, и после этого выразить .

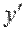13. Первая, вторая производные параметрически заданной функции.

Дифференцирование по переменной будем обозначать подстрочным значком (это обозначение общепринято). Тогда используя правила дифференцирования сложной функции и дифференцирование обратной функции, получим формулы для первой производной

для второй производной

14. ﾄифференциал функции и его вычисление.

Дифференциалом функции у=ƒ(х) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dу (или dƒ(х)):

dy=ƒ'(х)•∆х

15. Правила Лопиталя

Правило Бернулли-Лопита́ля — метод нахождения пределов функций, раскрывающий неопределённости вида 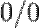и 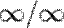. Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.

16. ﾏроизводные и дифференциалы высших порядков.

Дифференциалом порядка n, где n > 1 от функции 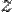в некоторой точке называется дифференциал в этой точке от дифференциала порядка (n — 1) то есть

.

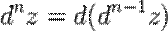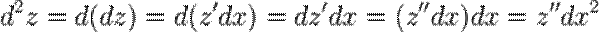
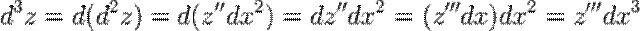
17. Признаки возрастания и убывания функции. Экстремумы функции.

Достаточное условие возрастания или убывания функции выражается следующей теоремой.

Теорем. Если на данном промежутке производная положительна, то функция возрастает в этом промежутке; если производная функции отрицательна, то функция убывает.

Замечание. Теорема имеет простой геометрический смысл. Если в некотором промежутке касательная к графику функции у = f(x) образует с осью Ох острый угол a (tg а > 0), то функция возрастает в этом промежутке (а). Если касательная к графику образует с осью Ох тупой угол a (tg а < 0), то функция убывает

Экстре́мум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.

18. Изогнутость графика функции. Точки перегиба.

точки через которые функция меняет выпуклость на выгнутость, а вторая производная меняет свой знак назыв точками перегиба.

19. Асимптоты кривой.

Асимптоты бывают:

А)вертикальные x=a, если точка x=a является точкой разрыва 2 рода, т.е. lim стремится к бесконечности

Б)наклонные y=kx+b

В) горизонтальные y=b

Замечание: вертикальные и горизонтальные асимптоты строят пунктирными линиями и никогда график функции их не пересекают, а наклонные асимптоты

20. Наибольшие и наименьшие значения функции на отрезке.

Наибольшим значением функции y = f(x) на промежутке X называют такое значение 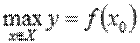, что для любого 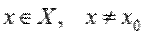справедливо неравенство .

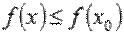Наименьшим значением функции y = f(x) на промежутке X называют такое значение 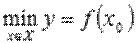, что для любого 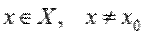справедливо неравенство .

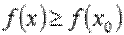21. ﾏервообразная и неопределенный интеграл и его свойства.

Первообразной функцией для функции f(x) называется такая функция F(х), производная которой равна данной функции где F'(x) = f(x). Функция f(x) называется подынтегральной функцией, а выражение f(x)dx - подынтегральным выражением.

F'(x) = f(x)

Неопределённый интегра́л для функции 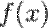— это совокупность всех первообразных данной функции.

1°. Производная неопределенного интеграла равна подынтегральной функции; дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е.

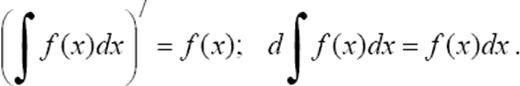
2°. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т.е.

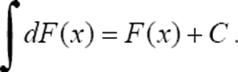
3°. Постоянный множитель можно вынести из под знака интеграла, т.е. если k = const ≠ 0, то

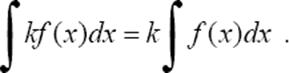
4° . Неопределенный интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций в отдельности.

22. Простейшие приемы интегрирования.

1.табличное интегрирование-непосредственное применение таблицы неопределенных интегралов

2.способ разложения-непосредственное применение 4 св-ва(интеграл от алгебраической суммы, конечного числа слагаемых равен алгебраической сумме интегралов от каждого слагаемого)

3.метод подведения под знак дифференциала в тождественное преобразования подынтегрального выражения и приведения его к табличному виду.

23. Метод интегрирования по частям

Интегри́рование по частя́м — один из способов нахождения интеграла. Суть метода в следующем: если подынтегральная функция может быть представлена в виде произведения двух непрерывных и гладких функций

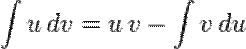
24. Метод замены переменной

Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся.

Один из способов интегрирования – метод замены переменной – реализуется с помощью формулы

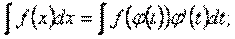
здесь переменная интегрирования х была заменена на новую переменную, t, с помощью (непрерывно дифференцируемой) функции
х = φ(t).

25. Задача, приводящая к понятию определенного интеграла

о площади криволинейной трапеции, о массе стержня и о перемещении точки.