Определители второго порядка

ВВЕДЕНИЕ

Настоящие методические указания предназначены для студентов всех специальностей и направлений бакалаврской подготовки заочной формы обучения, выполняющих расчетно-графическую работу по линейной алгебре, аналитической геометрии и введению в анализ. Приведенные краткие теоретические сведения, типовые задачи и примеры по каждому разделу позволяют успешно справиться с аналогическими заданиями самостоятельно и способствуют формированию предметного представления о соотношении теоретических и практических результатов.

ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЕЙ

Определители второго порядка

Определителем второго порядка 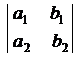называется число:

.

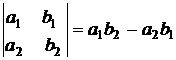Определение показывает несложность вычисления определителей второго порядка.

Примеры.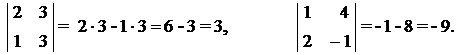

Определители третьего порядка

Определителем третьего порядка 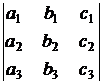называется число, которое может быть вычислено по следующему правилу (правило Саррюса): к определителю справа приписывается первый и второй столбцы и элементы, стоящие на диагоналях полученной таблицы, перемножаются, а затем эти произведения складываются, причем произведения элементов на диагоналях, идущих снизу вверх, берутся со знаком минус:

_.

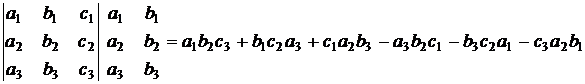Примеры.

а) -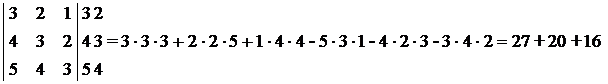

-15-24-24=0

б)

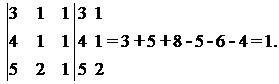
1.3. Задачи для самостоятельного решения

Вычислить определители второго и третьего порядка:

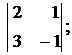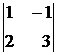а) б) ; в)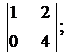

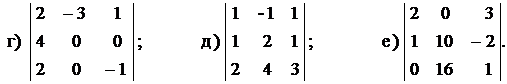
МАТРИЦЫ И ОПЕРАЦИИ НАД НИМИ

Понятие матрицы

Матрицей порядка n´m называется прямоугольная таблица чисел вида

.

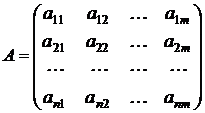Числа а_ij называются элементами матрицы. Матрицу будем коротко записывать 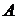= (а_ij) _n´m . Если n=m, то матрица называется квадратной порядка n.

Матрица 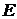с элементами (i,j=1,2,…,n) называется единичной матрицей n-го порядка.

Умножение матрицы на число

Чтобы умножить матрицу А на число l, необходимо умножить каждый элемент матрицы на это число.

Пример. Для матрицы 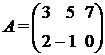найдем произведение 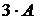. Из определения получаем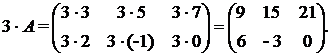

Сложение матриц

Если матрица В = (b_ij)_n´m имеет тот же порядок, что и матрица А = =(а_ij)_n´m, то можно определить их сумму - матрицу С = А + В = (c_ij)_n´m того же порядка - по правилу: с_{ij =} а_ij + b_ij для i =1, 2,..., n; j = 1, 2,..., m. Матрицы различных порядков складывать нельзя.

Пример. Найдем сумму матриц А + В, где

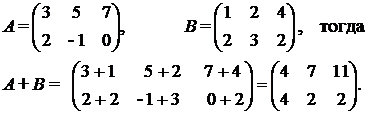
Умножение матриц

Произведением матрицы А = (а_ij)_n´m на матрицу В = (b_ij)_m´p называется матрица С = А´ В = (с_ij)_n´p, построенная по правилу

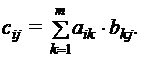
Практически перемножение матриц осуществляется следующим образом: берут i-ю строку матрицы А, умножают ее поэлементно на j-й столбец матрицы В и эти произведения складывают. Полученное число является элементом матрицы С, стоящим в i-й строке и j-м столбце.

Пример. Найдем произведение матриц АВ, если

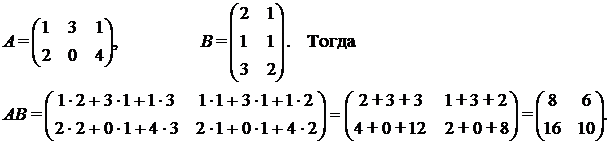
Внимание:

а) матрица А имеет порядок n´m, матрица В имеет порядок m´p, а их произведение АВ - порядок n´p;

б) в общем случае АВ ¹ ВА.

Примеры.

а) Найдем ВА, где матрицы А и В взяты из предыдущего примера:

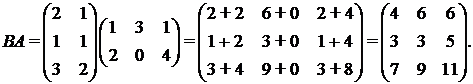
б) Найдем значение матричного многочлена В = 2А² + 3А + 5Е, где

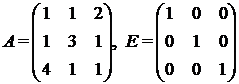- единичная матрица третьего порядка.

Имеем

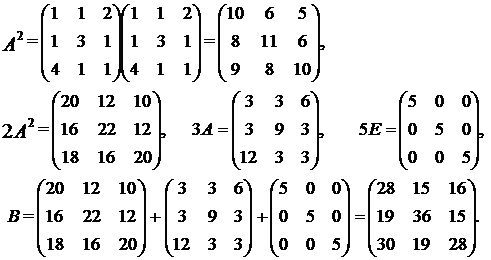тогда

2.5. Задачи для самостоятельного решения

а) Найти произведение матриц АВ, где

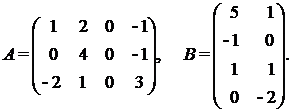
б) Найти произведения АВ и ВА, где

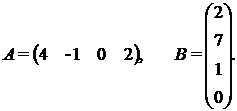
в) Найти значение выражения 3А – 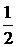ВС, где

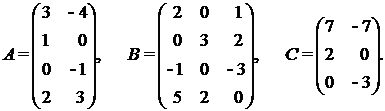
Обратная матрица

Для квадратной матрицы А порядка n можно определить такую матрицу Х порядка n, что ХА = АХ = Е, где Е - единичная матрица порядка n.

Матрица Х называется обратной к матрице А и обозначается А^-1.

Следующие условия являются необходимыми и достаточными, чтобы у матрицы А = (а_ij)_n´m была определена обратная матрица:

а) n=m;

б) определитель матрицы А не равняется нулю:

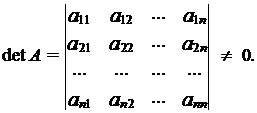
Следующие преобразования строк матрицы называются элементарными:

а) умножение любой строки на число, отличное от нуля;

б) прибавление к строке другой строки, домноженной на любое число;

в) перестановка строк;

г) отбрасывание нулевой строки.

Для нахождения обратной матрицы А^-1 применяется следующее правило:

а) выписывается матрица

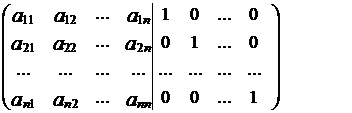(2.1)

б) с помощью элементарных преобразований над строками матрицы (2.1) превращают ее левую половину в единичную матрицу. Тогда ее правая половина превращается в обратную к ней матрицу А^-1.

Примеры.

а) Для матрицы 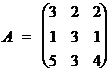найдем обратную.

По приведенному выше правилу получаем:

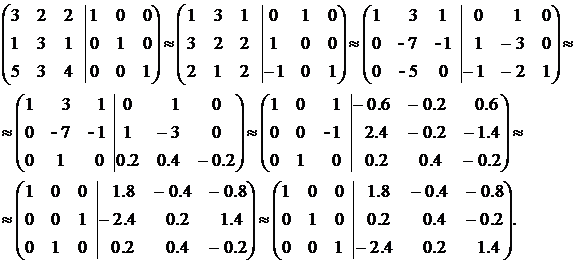
Итак, обратная матрица А^-1 равна

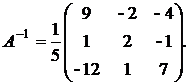
б) Решим матричное уравнение ХА + В = С, где

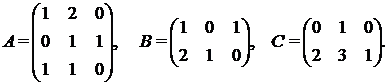
Умножим уравнение справа (порядок важен) на матрицу А^-1. Тогда

ХАА^-1 + ВА^-1 = СА^-1. Так как АА^-1 = Е, то ХЕ + ВА^-1 = СА^-1 или

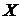= СА^-1- - ВА^-1 =(С-В)А^-1.

Найдем разность матриц

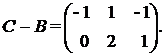
Вычислим матрицу А^-1

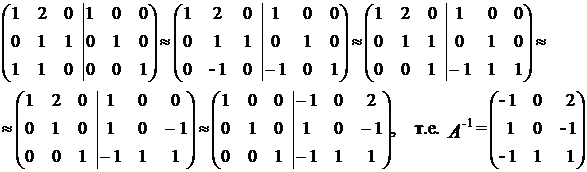
Тогда Х = (С-В)А^-1 =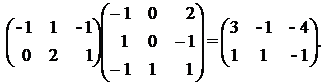

2.7. Задачи для самостоятельного решения

а) Найти А^-1, где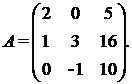

б) Решить матричное уравнение АХ =В, где

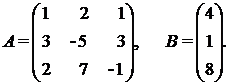
РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ

Линейные системы уравнений

Дана система m уравнений с n неизвестными

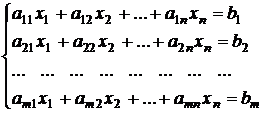. (3.1)

Решением этой системы называется любая совокупность n чисел (a₁, a₂,..., a_n), которая при подстановке в систему вместо совокупности неизвестных обращает каждое уравнение системы в тождество. Система (3.1) называется совместной, если она имеет хотя бы одно решение. В противном случае она называется несовместной..

Матрицы

называются соответственно матрицей и расширенной матрицей

системы (3.1).

Исследование на совместность и решение системы производят обычно одновременно с помощью метода Гаусса. Напомним, что элементы а_ii в матрице А называются диагональными. Метод Гаусса заключается в элементарных преобразованиях строк матрицы А₁ так, чтобы элементы преобразованной матрицы, стоящее ниже диагональных элементов, были нулевыми. При этом необходимо следить за диагональными элементами: они не должны обращаться в нуль. Если же при элементарных преобразованиях строк какой-либо диагональный элемент обратится в нуль (например, а_ii = 0), то поступать необходимо следующим образом: а) если в этом же столбце (где диагональный элемент оказался равен нулю) имеется ниже диагонального элемента ненулевой элемент, то соответствующую строку меняют местом с i-й строкой и продолжают преобразования; б) если же ниже нулевого диагонального элемента все элементы нулевые, то мы должны перейти к построению ступенчато-диагональной матрицы. Для этого сдвигаемся на один столбец вправо и считаем, что и диагональ матрицы тоже сдвинулась вправо и далее поступаем как описано выше. После всех преобразований матрица системы должна принять так называемый диагонально ступенчатый вид:

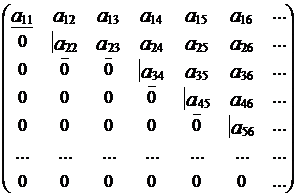
Ступенек в преобразованной матрице может быть несколько, причем разной длины. Элементы, которые будут стоять в углах таких ступенек, назовем ступенчато-диагональными (в данном примере это: а₁₁, а₂₂, а₃₄, а₄₅, а₅₆, ...).

Примеры.

а) Проверим совместность системы

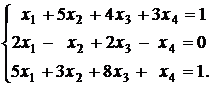
Для этого запишем расширенную матрицу системы и проведем элементарные преобразования над строками:

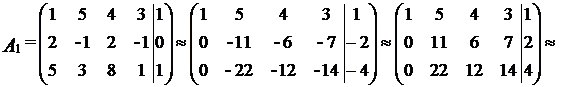
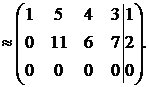
Из сказанного выше вытекает, что данная система совместна.

б) Исследуем на совместность систему

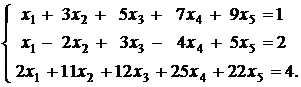
Записав расширенную матрицу системы, с помощью элементарных преобразований получаем

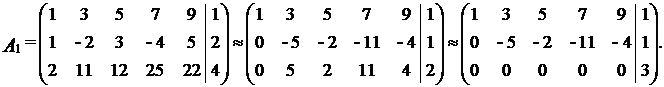
Таким образом, данная система несовместна.

Решение системы уравнений

После выяснения совместности системы строят ее общее решение. Для этого вновь полученную после элементарных преобразований матрицу записывают в виде системы, отбросив нулевые строки. Количество уравнений в этой системе определяет количество основных неизвестных. Все остальные неизвестные считаются свободными, им придаются произвольные значения. В качестве основных неизвестных берут неизвестные при ступенчато-диагональных элементах.

Примеры.

а) Построим общее решение системы из первого примера предыдущего пункта. После элементарных преобразований (см. выше) получаем систему

.

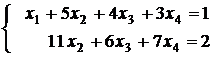Уравнений два, поэтому считаем х₁ и х₂ (стоящие при ступенчато-диаго-нальных элементах) основными, а х₃ и х₄ свободными. Находим из системы основные неизвестные через свободные:

,

.

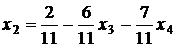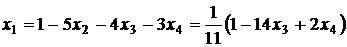Таким образом, общее решение системы имеет вид:

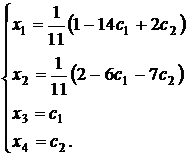
б) Решим систему

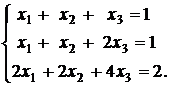
Записываем расширенную матрицу системы и преобразуем ее

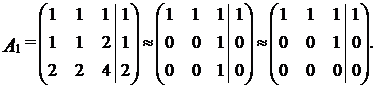
Выбираем в качестве основных переменные х₁ и х₃, как стоящие при ступенчато-диагональных элементах, переменная х₂ берется свободной. Итак,

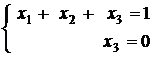
и общее решение системы

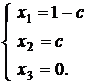
3.3. Задачи для самостоятельного решения

Исследовать и в случае совместности решить предлагаемые ниже системы линейных уравнений.

а) 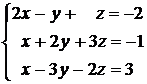б)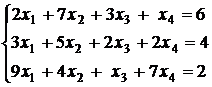

в)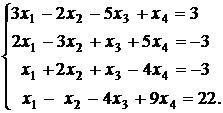

Основные понятия

Понятие вектора известно из школьного курса. Наиболее часто мы будем пользоваться координатной формой записи векторов: 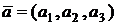. Напомним, что всегда вектор предполагается свободным, т.е. его можно без изменения длины и направления переносить в любую точку пространства. В случае координатного задания вектора его длина вычисляется по формуле:

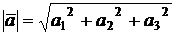. (4.1)

Направление же вектора определяется углами a, b, g, образованными вектором с положительными полуосями координат Ох, Оу, Oz, которые можно найти из формул для направляющих косинусов этих углов:

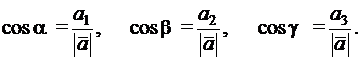(4.2)

Операции над векторами

Произведение вектора на скалярный множитель l определяется по формуле l = (lа₁, lа₂, lа₃).

Для двух векторов 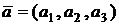, 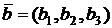их сумма и разность определяются по правилам:

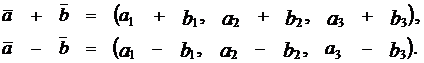
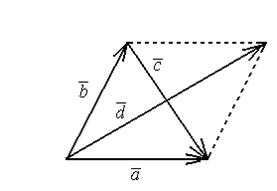
Геометрически сумма и разность векторов строится как на рисунке:

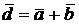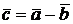Если точка О - начало координат, а М - точка с координатами (x, y, z), то вектор 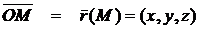называется радиусом-вектором точки М.

Вектор 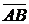с началом в точке А(x₁, y₁, z₁) и концом в точке В(x₂, y₂, z₂) в координатном виде записывается так: = .

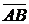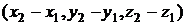Примеры.

а) В треугольнике АВС сторона АВ точками М и N разделена на три равные части: 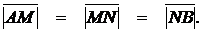Найти вектор 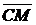, если 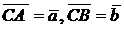. Если построить треугольник и указанные вектора, то из геометрических правил сложения и вычитания легко получаются равенства 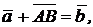т.е. 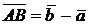. Так как 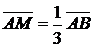, то 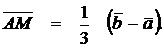Та-ким образом,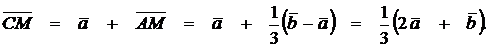

б) Найти длину вектора = (10, 15, -30) и его направляющие косинусы.

По формулам (4.1) и (4.2) определяем

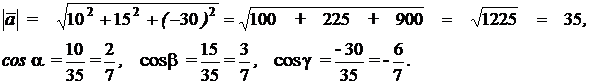
3) Найти вектор 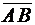, если А(2, 1, 0) и В(3, 0, 5).

Из формулы для координат вектора 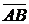имеем 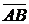= (3-2, 0-1, 5-0) =

= (1, -1, 5).

4.3. Задачи для самостоятельного решения

а) Дан треугольник АВС. На стороне ВС расположена точка М так, что 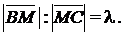Найти вектор 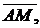если = ,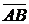

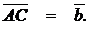
б) Найти координаты вектора 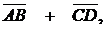где А(0, 0, 1), В(3, 2, 1), С(4, 6, 5), D(1, 6, 3).

в) Даны радиусы - векторы вершин треугольника АВС: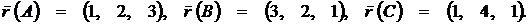

Показать, что треугольник АBC - равносторонний.

г) Вычислить длину вектора (1, 2, 1) и найти его направляющие косинусы.

д) Даны точки А(1, 2, 3) и В(3, -4, 6). Найти длину и направление вектора .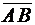

Определение и свойства

Пусть даны два вектора и 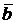.Тогда их скалярное произведение определяется из равенства 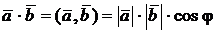, где j - угол между этими векторами.

Если векторы заданы в координатной форме 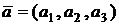, , 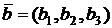то их скалярное произведение вычисляется по формуле:

.

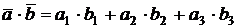Скалярное произведение векторов обладает следующими свойствами:

а) ;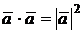

б) если ^ 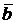(ортогональные вектора), то 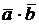= 0;

в) ;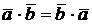

г) ;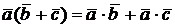

д) 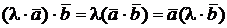, где λ- любое число.

Примеры.

а) Найти скалярное произведение векторов = (2, 1, 1) и 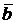= (2, -5, 1).

Из определения имеем = .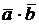

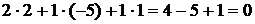б) Даны вектор = (m, 3, 4) и вектор 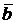= (4, m, -7). При каких значениях m вектор ортогонален вектору ?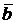

Из условий ортогональности имеем: 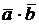= 4m + 3m -28 = 0,

7m = 28, m = 4.

в) Найти 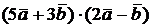, есл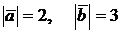и и ^ .

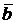Из свойств скалярного произведения имеем: ,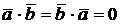

т.к. ^ 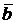, тогда

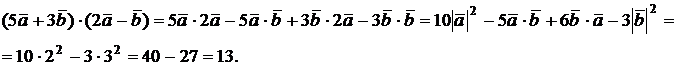
г) Определить угол между векторами = (1, 2, 3) и 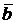= (0, 4, -2).

Так как 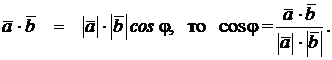Из координатного представления векторов находим 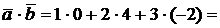0+8-6=2,

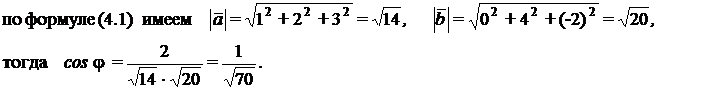
5.2. Задачи для самостоятельного решения

а) Даны векторы = (3, -2, -4), 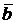= (6, -2, 3). Найти ( )( ).

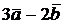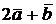б) Вычислить работу силы 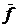= (1, 2, 1) при перемещении материальной точки из положения М₁(-1, 2, 0) в положение М₂(2, 1, 3) . Напомним, что работа вектора силы 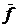равна скалярному произведению вектора 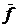на вектор перемещения _.

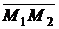в) Найти координаты вектора 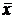, если он коллинеарен вектору

= (2, 1, 0) и его скалярное произведение на вектор равно 3, т.е.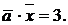

ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ

Определение и свойства

Смешанным произведением трех векторов

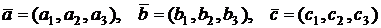называется число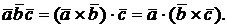

Смешанное произведение обладает следующими свойствами:

а) 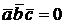, если все три вектора параллельны одной и той же плоскости (компланарны);

б)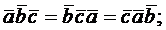

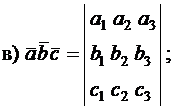
г) объем параллелепипеда, построенного на векторах 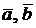и 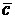, равен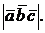

Примеры.

а) Найти смешанное произведение векторов =(5, 7, 2), 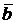= (1, -1, 1),

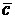= (2, 2, 1).

Из определения имеем

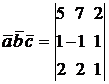= -5 + 14 + 4 + 4 - 10 - 7 = 0, т.е. вектора 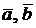и 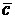компланарны.

б) Найти объем треугольной пирамиды с вершинами А(2, 2, 2),

В(4, 3, 3), С(4, 5, 4), D(5, 5, 6).

Из свойств смешанного произведения заключаем, что искомый объем равен

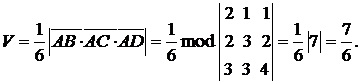
в) Вычислим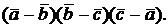

Используя определение смешанного произведения и свойства векторного и скалярного произведений получаем

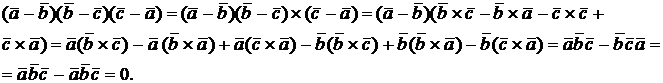
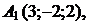
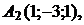
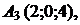
г) По координатам вершин пирамиды 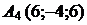найти: 1) длины ребер 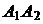и 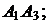2) угол между ребрам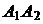и и 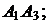3) площадь грани 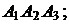4) объем пирамиды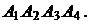

Находим векторы 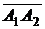и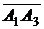

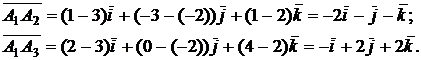
Длины векторов, т.е. длины ребер 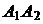и 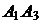, таковы:

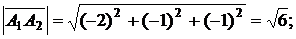
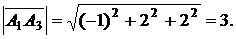
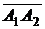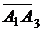Скалярное произведение векторов и равно

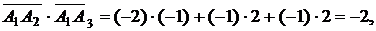
а косинус угла между ними:

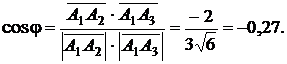
Отсюда следует, что 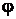- тупой угол, равный 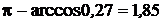(рад.) с точностью до 0,01. Это и есть искомый угол между ребрам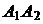и и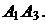

Площадь грани 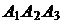равна половине площади параллелограмма, построенного на векторах 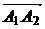и 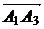, т.е. половине модуля векторного произведения этих векторов:

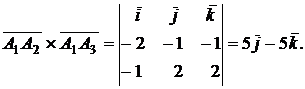
Следовательно,

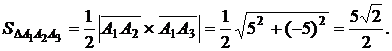
Объем 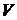пирамиды равен 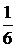объема параллелепипеда, построенного на векторах 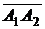, , 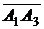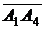. Вектор 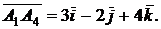Итак,

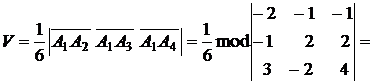
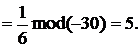
7.2. Задачи для самостоятельного решения

а) Даны векторы = (1, 1, -3), 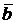= (-2, 2, 1) и 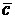= (3, -2, 5). Вычислить .

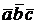б) В треугольной пирамиде с вершинами в точках А(1, 1, 1), В(2, 0, 2), С(2, 2, 2) и D(3, 4, -3) вычислить высоту h = | |.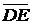

в) Доказать, что четыре точки А(1, 2, 1), В(0, 1, 5), С(-1, 2, 1) и

D(2, 1, 5) лежат в одной плоскости.

ПРЯМАЯ НА ПЛОСКОСТИ

Или

у - у₀ = k (х - х₀) 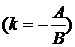. (8.9)

Уравнение прямой, проходящей через две точки (х₀, у₀) и (х₁, у₁) записывается в виде

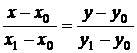или 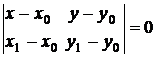(8.10)

Пример. Составим уравнение прямой, проходящей через точки

(-1, 3) и (2, 5).

Из (8.9) имеем 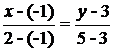или (х + 1)/3 = (у - 3)/2, или

2х - 3у + 11 = 0.

8.2. Задачи для самостоятельного решения

а) Написать уравнение прямой и привести его к общему виду, если

1) прямая проходит через точку М(-1, 2) перепендикулярно вектору

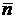= (2, -3);

2) прямая проходит через точку М(-1, 1) параллельно вектору

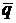= (2, 0);

3) прямая проходит через точки М₁(1, 2) и М₂(-1, 0).

б) Составить уравнение прямой, которая проходит через точку М(8, 6) и отсекает от координатного угла треугольник с площадью, равной 12 кв. ед.

Уравнений прямой

В различных геометрических задачах используются те или иные уравнения прямой в зависимости от условий. При этом важно помнить геометрический смысл различных коэффициентов в уравнении прямой. Наиболее часто используются следующие два факта: в общем уравнении прямой (8.1) коэффициенты при неизвестных образуют вектор 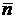= (А, В), ортогональный к этой прямой (вектор нормали); в уравнении

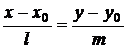
вектор 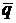= (l, m) параллелен этой прямой (направляющий вектор), а прямая проходит через точку (х₀, у₀).

Примеры.

а) Составим уравнение прямой, проходящей через точку (-2, -5), и параллельной прямой 3х + 5у + 2 = 0.

Из уравнения (8.8) имеем А(х+2)+В(у+5)=0. Из условия параллельности прямых заключаем, что ортогональные им вектора 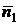= (3, 5) и 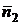= (А, В) также параллельны. Следовательно, можно положить 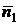= = 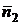(3, 5) (длина вектора нормали не имеет значения). Итак, нужная нам прямая имеет уравнение:

3(х + 2) + 5(у + 5) = 0 или 3х + 5у + 31 = 0.

б) Даны вершины треугольника А(2, 2), В(-2, -8), С(-6, -2). Составим уравнение медиан треугольника.

Медиана проходит через вершину А и делит отрезок ВС пополам. Определим координаты середины отрезка ВС: х₀ = ((-2) + (-6))/2 = -4,

у₀ = ((-8) + (-2))/2 = -5. Пользуясь теперь уравнением прямой (8.10), проходящей через две точки, получаем уравнение медианы, проходящей через вершину А: (х + 4)/6 = (у + 5)/7 или 7х - 6у - 2 = 0.

Аналогично находим урвнения остальных медиан:

х₁ = 0, у₁ = -3, (х + 6)/6 = (у + 2)/(-1), х + 6у + 18 = 0,

х₂ = -2, у₂ = 0, (х + 2)/0 = (у + 8)/8, х + 2 = 0.

в) Даны вершины треугольника А(0, 1), В(12, -1), С(6, 5). Составим уравнение высоты треугольника, проведенной из вершины С.

Высота проходит через точку С, следовательно, ее уравнение можно записать в виде К(х - 6) + М(у - 5) = 0. Найдем координаты вектора нормали (К, М): так как наша прямая ортогональна стороне АВ треугольника АВС, то вектор, соединяющий точки А и В, является ортогональным прямой, его и можно взять в качестве вектора-нормали: (12 - 0, -1 - 1) = (12, -2). Итак, уравнение прямой имеет вид: 12(х - 6) - 2(у - 5) = 0 или 12х - 2у -62 = 0.

8.5. Задачи для самостоятельного решения

а) Вычислить расстояние от прямой 2х - у + 1 = 0 до начала координат и до точки М(-1, 2).

б) В треугольнике с вершинами А(1, 2), В(2, -2), С(6, 1) найти:

1) уравнение стороны АВ;

2) уравнение высоты, проходящей через вершину С, и вычислить ее длину;

3) найти угол между этой высотой и медианой, проходящей через точку В.

в) Даны две вершины треугольника А(-10, 2) и B(6, 4); его высоты пересекаются в точке М(5, 2). Определить координаты третьей вершины С.

Плоскость в пространстве

При рассмотрении плоскости в пространстве необходимо иметь в виду, что методика решения задач аналогична методике решения задач на прямую в плоскости. Это связано с тем, что различные уравнения плоскости в пространстве подобны уравнениям прямой на плоскости.

Приведем уравнения плоскости в пространстве:

- общее уравнение плоскости

- Ах + Ву + Сz + D = 0, (9.1)

где 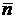= (А, В, С) – вектор, ортогональный плоскости (вектором нормали);

-уравнение плоскости в отрезках

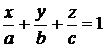, (9.2)

где 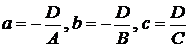, причем (а, 0, 0), (0, в, 0), (0, 0, с) - координаты точек пересечения плоскости с осями координат;

- уравнение плоскости, проходящей через точку (х₀, у₀, z₀) с вектором нормали 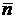= (А, В, С)

А(х - х₀) + В(у - у₀) + С(z - z₀) = 0, (9.3)

- нормальное уравнение плоскости

хcos a + уcos b + zcos g - p = 0, (9.4)

где р - расстояние от плоскости до начала координат, a, b, g - углы между координатными осями и вектором нормалью к плоскости, направленным от начала координат к плоскости;

- уравнение плоскости, проходящей через три точки (х₁, у₁, z₁), (х₂, у₂, z₂),

(х₃, у₃, z₃)

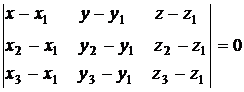(9.5)

Приведение общего уравнения плоскости (9.1) к нормальному виду (9.4) осуществляется домножением на множитель:

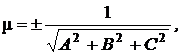
где знак выбирается из условия mD<0.

Расстояние d от точки (х₀, у₀, z₀) до плоскости (9.1) вычисляется по формуле:

d = 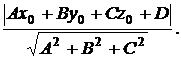(9.6)

Угол между плоскостями А₁х + В₁у + С₁z + D₁ = 0 и

А₂х + В₂у + С₂z + D₂ = 0 определяется из формулы:

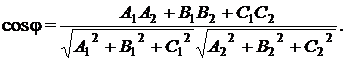(9.7)

Условие параллельности плоскостей:

А₁/А₂ = В₁/В₂ = С₁/С₂, (9.8)

и условие ортогональности:

А₁А₂ + В₁В₂ + С₁С₂ = 0. (9.9)

Примеры.

а) Приведем уравнение плоскости 2х + 4у - 5z + 21 = 0 к нормальному виду.

Домножив уравнение на нормирующий множитель

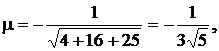
где знак минус взят, так как D>0, получим нормальное уравнение плоскости в виде

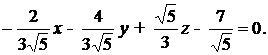
б) Составим уравнение плоскости, проходящей через точку (1, 2, 3) и ортогональную вектору (3, 2, 1).

Из уравнения (9.3) и геометрического смысла коэффициентов уравнения сразу имеем 3(х - 1) + 2(у - 2) + (z - 3) = 0 или

3х + 2у + z - 10 = 0.

в) Найдем уравнение плоскости, проходящей через точку (3, 2, -1) и параллельную плоскости 3х - 5у + 2z - 10 = 0.

В силу параллельности плоскостей векторы нормали у обеих плоскостей можно взять равными, т.е. вектор (3, -5, 2) является вектором нормали нашей плоскости. Тогда из уравнения (9.3) имеем

3(х - 3) - 5(у - 2) + 2(z + 1) = =0 или 3х - 5у + 2z + 3 = 0.

г) Найдем уравнение плоскости, проходящей через точки А(2, -1, 4) и В(3, 2, -1) перпендикулярно плоскости х + у + 2z - 3 = 0.

Для нахождения уравнения заданной плоскости нам необходимо найти вектор нормали 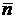этой плоскости. Так как он ортогонален нашей плоскости, то он ортогонален любому вектору, параллельному этой плоскости. Таким образом, вектор нормали 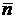ортогонален векторам 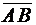и вектору нормали плоскости х + у + 2z - 3 = 0, т.е. 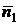= (1, 1, 2). Из свойств векторного произведения вытекает, что в качестве вектора нормали нашей плоскости можно взять вектор 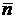= 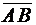´ 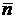₁.

Итак,

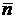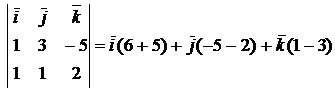= = (11, -7, -2).

Из (9.3) теперь легко имеем 11(х - 2) - 7(у + 1) - 2(z - 4) = 0 или

11х - 7у - 2z -21 = 0.

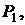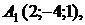
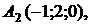
д) Найти угол между плоскостью проходящей через точки 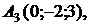и плоскостью 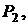заданной уравнением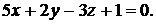

Взяв текущую точку 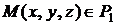и определив вектора 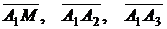, уравнение плоскости 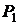находим по формуле (9.5):

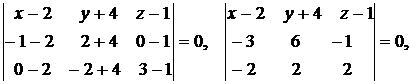
т.е.

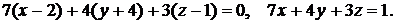
По уравнению плоскостей определяем их нормальные векторы: