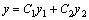Уравнения высших порядков.случаи понижения порядка
14.4.2. Некоторые типы уравнений, допускающие понижение порядка.
 14.4.2.1. Уравнение вида
14.4.2.1. Уравнение вида 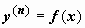 решается последовательным n-кратным интегрированием. Пример:
решается последовательным n-кратным интегрированием. Пример:
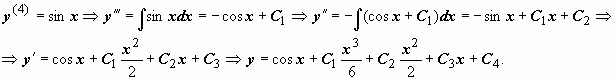
Переобозначив постояные, общее решение запишем в виде y = cos x + C1x3 + C2x2 + C3x + C4.
 14.4.2.2. Уравнение, не содержащее в явном виде неизвестную функцию и её младшие производные. Порядок уравнения вида F(x, y(k), y(k+1), y(k+2), …,y(n)) = 0, не содержащего функции y(x) и k - 1 младшую производную этой функции в явном виде, может быть понижен ровно на k единиц введением новой неизвестной функции z(x) = y(k)(x). Тогда
14.4.2.2. Уравнение, не содержащее в явном виде неизвестную функцию и её младшие производные. Порядок уравнения вида F(x, y(k), y(k+1), y(k+2), …,y(n)) = 0, не содержащего функции y(x) и k - 1 младшую производную этой функции в явном виде, может быть понижен ровно на k единиц введением новой неизвестной функции z(x) = y(k)(x). Тогда 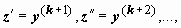 z(n-k) = y(n)(x), и относительно z(x) уравнение примет вид
z(n-k) = y(n)(x), и относительно z(x) уравнение примет вид 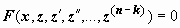 , т.е. будет уравнением n - k-го порядка. После нахожденияz(x) последовательным интегрированием решается уравнение y(k) = z(x).
, т.е. будет уравнением n - k-го порядка. После нахожденияz(x) последовательным интегрированием решается уравнение y(k) = z(x).
 Пример: решить задачу Коши:
Пример: решить задачу Коши: 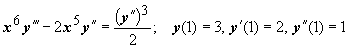 .
.
 Младшая производная, входящая в явной форме в уравнения, - вторая, поэтому делаем замену искомой функции
Младшая производная, входящая в явной форме в уравнения, - вторая, поэтому делаем замену искомой функции 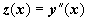 . Тогда
. Тогда 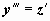 , и уравнение примет вид
, и уравнение примет вид 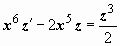 . Это - уравнение Бернулли; пусть z = uv, тогда
. Это - уравнение Бернулли; пусть z = uv, тогда 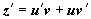 ,
, 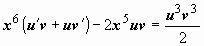 ,
, 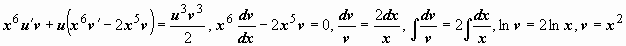 ,
, 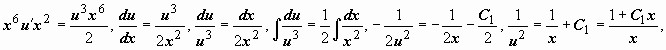
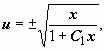 следовательно,
следовательно, 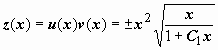 . Относительно y(x)- это уравнение
. Относительно y(x)- это уравнение 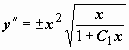 . Мы можем последовательно находить
. Мы можем последовательно находить 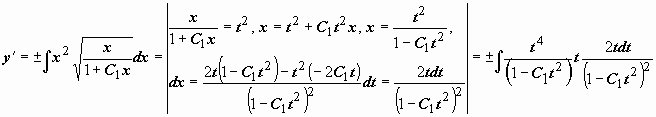 и так далее, однако в этом нет необходимости. Так как мы решаем задачу Коши, то из начального условия
и так далее, однако в этом нет необходимости. Так как мы решаем задачу Коши, то из начального условия 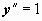 при x = 1 можно определить и знак частного решения, и значение постоянной C1:
при x = 1 можно определить и знак частного решения, и значение постоянной C1: 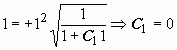 . Теперь
. Теперь 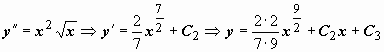 . Из условия
. Из условия 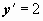 при x = 1 находим C2:
при x = 1 находим C2: 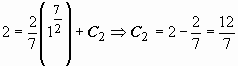 ; из условия y = 3 при x = 1 находим C3:
; из условия y = 3 при x = 1 находим C3: 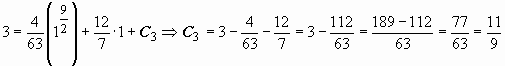 . Окончательный ответ:
. Окончательный ответ: 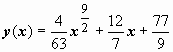 .
.
 14.4.2.3. Уравнение, не содержащее в явном виде независимую переменную x.Порядок уравнения
14.4.2.3. Уравнение, не содержащее в явном виде независимую переменную x.Порядок уравнения 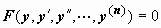 , не содержащего явно x, может быть понижен на 1 с помощью красивого искусственного приёма, который заключается в том, что вводится новая функциональная зависимость
, не содержащего явно x, может быть понижен на 1 с помощью красивого искусственного приёма, который заключается в том, что вводится новая функциональная зависимость 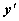 от y:
от y: 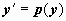 . Старшие производные y по xвычисляются по правилу дифференцирования сложной функции:
. Старшие производные y по xвычисляются по правилу дифференцирования сложной функции: 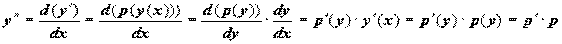 .
.
Аналогично, 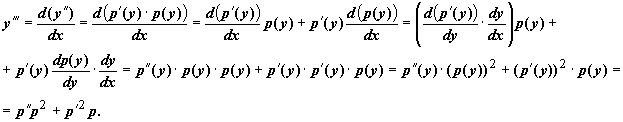
Также находятся следующие производные, и всегда k -ая производная y по x выражается через k-1 -ую производную p по y. В случае уравнения второго порядка 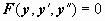 в результате таких преобразований получим
в результате таких преобразований получим 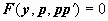 , т.е. уравнение первого порядка (в котором y выступает как аргумент, p(y) - как неизвестная функция). После нахождения решения p = p(y, C1) этого уравнения решается уравнение
, т.е. уравнение первого порядка (в котором y выступает как аргумент, p(y) - как неизвестная функция). После нахождения решения p = p(y, C1) этого уравнения решается уравнение 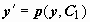 , решение которого y = y(x, C1, C2) будет общим решением исходного уравнения.
, решение которого y = y(x, C1, C2) будет общим решением исходного уравнения.
 Примеры: 1. Задача Коши
Примеры: 1. Задача Коши 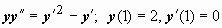 .
.
Переменная x явно в уравнение не входит, поэтому полагаем 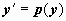 ,
, 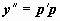 , тогда
, тогда 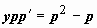 . Просто сократить на p это уравнение нельзя, так как можно потерять семейство решений
. Просто сократить на p это уравнение нельзя, так как можно потерять семейство решений 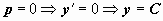 , поэтому рассматриваем два случая:
, поэтому рассматриваем два случая:
 1.
1. 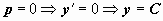 ;
;
 2.
2. 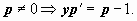 Это - уравнение с разделяющимися переменными:
Это - уравнение с разделяющимися переменными: 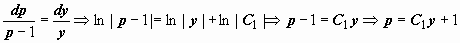 . Получено уравнение
. Получено уравнение 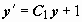 , решаем его:
, решаем его: 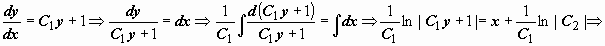
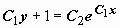 . Это общее решение уравнения, в данном случае оно включает в себя решение y = C при C2 = 0. Находим значения постоянных, при которых удовлетворяются начальные условия: из
. Это общее решение уравнения, в данном случае оно включает в себя решение y = C при C2 = 0. Находим значения постоянных, при которых удовлетворяются начальные условия: из 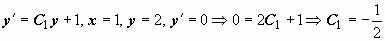 . Далее, из
. Далее, из 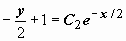 следует, что
следует, что 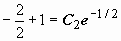 , т.е. C2 = 0. Частное решение -
, т.е. C2 = 0. Частное решение - 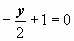 , т.е. y = 2.
, т.е. y = 2.
 Пример 2.
Пример 2. 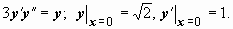
 Решение:
Решение: 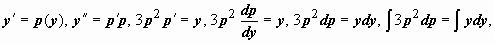
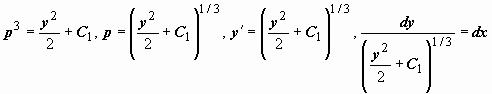 . Интеграл от дифференциала в левой части этого равенства вообще не берётся, поэтому проверим, не упростится ли задача, если использовать начальные условия. Так как при x = 0 должно быть
. Интеграл от дифференциала в левой части этого равенства вообще не берётся, поэтому проверим, не упростится ли задача, если использовать начальные условия. Так как при x = 0 должно быть 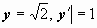 , то получим
, то получим 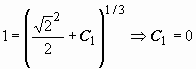 . Поэтому частное решение должно удовлетворять уравнению
. Поэтому частное решение должно удовлетворять уравнению 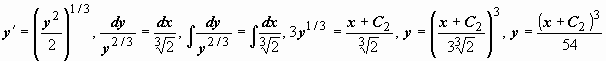 . Находим
. Находим 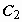 :
: 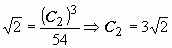 . Ответ: решение задачи Коши
. Ответ: решение задачи Коши 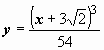 .
.
 14.4.2.4. Применение интегрируемых комбинаций.Иногда удаётся заметить, что в уравнении
14.4.2.4. Применение интегрируемых комбинаций.Иногда удаётся заметить, что в уравнении 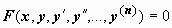 правая часть является производной некоторой функции
правая часть является производной некоторой функции 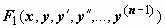 , т.е. уравнение имеет вид
, т.е. уравнение имеет вид 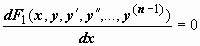 . Интегрируя по x, получим уравнение, порядок которого на единицу меньше порядка исходного уравнения (так называемый первый интеграл уравнения):
. Интегрируя по x, получим уравнение, порядок которого на единицу меньше порядка исходного уравнения (так называемый первый интеграл уравнения): 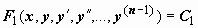 .
.
 Пример:
Пример: 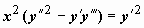 . Если переписать это уравнение в виде
. Если переписать это уравнение в виде 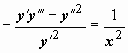 и сообразить, что справа стоит производная функции
и сообразить, что справа стоит производная функции 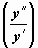 , то получим
, то получим 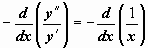 , откуда
, откуда 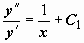 . Это уравнение не содержит явно y, поэтому
. Это уравнение не содержит явно y, поэтому 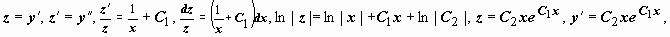
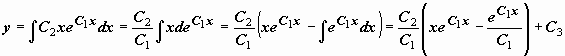 .
.
ЛОУ.Общие св-ва решений
| 3. Линейные однородные уравнения второго порядка. Общие свойства решений | ||||||||
Дифференциальное уравнение второго порядка называется линейным, если оно имеет вид:
то есть является линейным относительно неизвестной функции y и ее производных Если правая часть уравнения
и называется линейным однородным. Пусть Теорема 1. Если Так как
Подставим Теорема 2. Если Доказательство. Подставим Следствие. Если Определение. Два решения Если же таких чисел подобрать нельзя, то решения Очевидно, решения В самом деле, если Обратно, если Замечание. Из определения линейно независимых решений и рассуждений выше можно сделать вывод, что если Например, функции Теорема. Если Доказательство. В силу теорем 1 и 2 (и следствия к ним) Если решения В тоже время, если бы Итак, общее решение уравнения (9):
где |
19.Понятие линейно-независимой системы функций. определитель Вронского. достаточное условие линейной независимости. понятие фундаментальной системы функции. Примеры. Необходимое и достаточное условие отличия от нуля определителя Вронского на отрезке [а,в]
Понятие линейно-независимой системы функций 





Функции 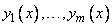 называются линейно зависимыми на
называются линейно зависимыми на  , если одна из них является линейной комбинацией других
, если одна из них является линейной комбинацией других 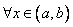 . Другими словами, функции
. Другими словами, функции 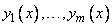 называются линейно зависимыми на
называются линейно зависимыми на  , если существуют числа
, если существуют числа 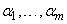 , из которых хотя бы одно не равно нулю, такие, что
, из которых хотя бы одно не равно нулю, такие, что
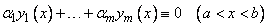 . (4)
. (4)
Если тождество (4) выполняется лишь в случае, когда все 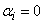 , то функции
, то функции 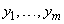 называются линейно независимыми на
называются линейно независимыми на  .
.
Система из 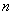 линейно независимых на интервале
линейно независимых на интервале  решений
решений
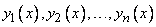
однородного дифференциального уравнения 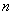 -го порядка (3) с непрерывными на
-го порядка (3) с непрерывными на  коэффициентами
коэффициентами 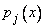 называется фундаментальной системой решений этого уравнения.
называется фундаментальной системой решений этого уравнения.
Чтобы решить линейное однородное дифференциальное уравнение 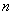 -го порядка (3) с непрерывными коэффициентами
-го порядка (3) с непрерывными коэффициентами 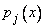 , надо найти его фундаментальную систему решений.
, надо найти его фундаментальную систему решений.
Согласно теореме 1 произвольная линейная комбинация из решений 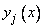 , т. е. сумма
, т. е. сумма
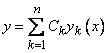 , (5)
, (5)
где 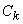 - произвольные числа, есть в свою очередь решение уравнения (3) на
- произвольные числа, есть в свою очередь решение уравнения (3) на  . Но оказывается, что и обратно, всякое решение дифференциального уравнения (3) на интервале
. Но оказывается, что и обратно, всякое решение дифференциального уравнения (3) на интервале  есть некоторая линейная комбинация из указанных (независимых между собой) его частных решений
есть некоторая линейная комбинация из указанных (независимых между собой) его частных решений 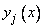 (см. ниже теорему 4), образующих фундаментальную систему решений.
(см. ниже теорему 4), образующих фундаментальную систему решений.
Таким образом, общее решение однородного дифференциального уравнения (3) имеет вид (5), где 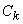 - произвольные постоянные, а
- произвольные постоянные, а 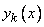 - частные решения (3), образующие фундаментальную систему решений однородного уравнения.
- частные решения (3), образующие фундаментальную систему решений однородного уравнения.
Отметим, что общее решение неоднородного уравнения (1) есть сумма какого-либо его частного решения 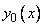 и общего решения однородного уравнения
и общего решения однородного уравнения
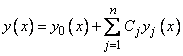 . (6)
. (6)
В самом деле,
 .
.
С другой стороны, если 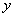 есть произвольное решение уравнения (1), то
есть произвольное решение уравнения (1), то
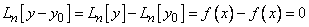 ,
,
и, следовательно, 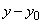 есть решение однородного уравнения; но тогда существует такие числа
есть решение однородного уравнения; но тогда существует такие числа 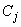 , что
, что
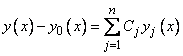 ,
,
т. е. для этих чисел выполняется равенство (6).
Определитель Вронского.
Теорема 2. Если функции 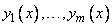 линейно зависимы на
линейно зависимы на  и имеют производные до
и имеют производные до 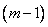 -го порядка, то определитель
-го порядка, то определитель
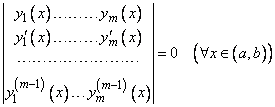 . (7)
. (7)
Яндекс.Директ Все объявления  Решение уравнений онлайн! Калькулятор ЛовиОтвет – решение уравнений одним кликом! Скачай бесплатно!loviotvet.ru Кто такой Иисус Как узнать, кто такой Иисус Христос на самом деле?godlovesrussia.com
Решение уравнений онлайн! Калькулятор ЛовиОтвет – решение уравнений одним кликом! Скачай бесплатно!loviotvet.ru Кто такой Иисус Как узнать, кто такой Иисус Христос на самом деле?godlovesrussia.com
Определитель (7) называется определителем Вронского или вронскианом и обозначается символом 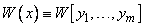 .
.
Доказательство. Так как функции 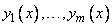 линейно зависимы на
линейно зависимы на  , то существуют такие не все равные нулю числа
, то существуют такие не все равные нулю числа 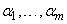 , при которых выполняется тождество (4) на
, при которых выполняется тождество (4) на  . Дифференцируя его
. Дифференцируя его 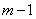 раз, получим систему уравнений
раз, получим систему уравнений
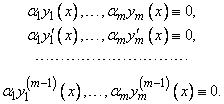
Эта однородная система по условию имеет нетривиальное решение 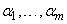 (т. е. хотя бы одно
(т. е. хотя бы одно 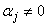 ) при
) при 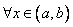 . Последнее возможно, когда определитель системы, который является определителем Вронского
. Последнее возможно, когда определитель системы, который является определителем Вронского 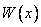 , тождественно равен нулю. Теорема доказана.
, тождественно равен нулю. Теорема доказана.
Замечание. Из теоремы 2 вытекает, что если 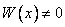 хотя бы в одной точке
хотя бы в одной точке  , то функции
, то функции 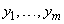 линейно независимы на
линейно независимы на  .
.
Пример 2. Функции 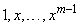 линейно независимы на любом
линейно независимы на любом  , так как
, так как
 .
.
Пример 3. Функции 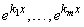 линейно независимы на любом
линейно независимы на любом  , если
, если 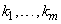 - различные числа (действительные или комплексные).
- различные числа (действительные или комплексные).
В самом деле.
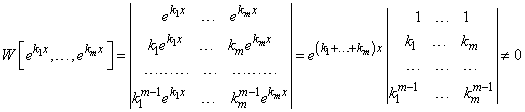 ,
,
так как последний определитель есть определитель Вандермонда, который при различных 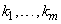 не равен нулю.
не равен нулю.
Пример 4. Функции 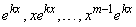 линейно независимы на любом
линейно независимы на любом  .
.
Так как 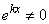 и
и
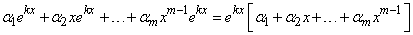 ,
,
то линейная независимость указанных функций вытекает из второго примера.
Теорема 3. Для того чтобы решения 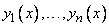 линейного дифференциального однородного уравнения
линейного дифференциального однородного уравнения 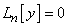 с непрерывными коэффициентами были линейно независимыми на
с непрерывными коэффициентами были линейно независимыми на  , необходимо и достаточно, чтобы
, необходимо и достаточно, чтобы 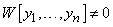 для всех
для всех 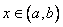 .
.
Доказательство. 1) Если 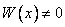 на
на  , то функции
, то функции 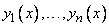 линейно независимы независимо от того, являются они решениями уравнения
линейно независимы независимо от того, являются они решениями уравнения 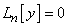 или нет (см. замечание).
или нет (см. замечание).
2) Пусть 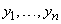 являются линейно независимыми функциями на
являются линейно независимыми функциями на  и являются решениями уравнения
и являются решениями уравнения 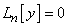 .
.
Докажем, что 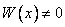 всюду на
всюду на  . Допустим противное, что существует точка
. Допустим противное, что существует точка 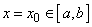 , в которой
, в которой 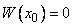 . Выберем числа
. Выберем числа 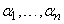 , одновременно не равные нулю, так, чтобы они были решениями системы
, одновременно не равные нулю, так, чтобы они были решениями системы
 (8)
(8)
Это можно сделать, так как определитель системы (8) есть 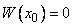 . Тогда в силу теоремы 1 функция
. Тогда в силу теоремы 1 функция 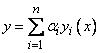 будет решением уравнения
будет решением уравнения 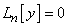 с нулевыми начальными условиями (по (8))
с нулевыми начальными условиями (по (8))
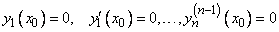 .
.
Но таким же условиям удовлетворяет и тривиальное решение 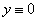 . В силу теоремы существования и единственности решение, удовлетворяющее этим
. В силу теоремы существования и единственности решение, удовлетворяющее этим 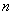 начальным условиям, может быть только одно, следовательно,
начальным условиям, может быть только одно, следовательно,  на
на  т. е. функции
т. е. функции 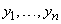 линейно зависимы на
линейно зависимы на  , что не предполагалось. Теорема доказана.
, что не предполагалось. Теорема доказана.
Если 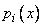 - разрывные функции в интервале, где мы ищем решение, то уравнение
- разрывные функции в интервале, где мы ищем решение, то уравнение 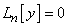 может иметь не одно решение, удовлетворяющее начальным условиям
может иметь не одно решение, удовлетворяющее начальным условиям 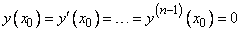 , и тогда возможно, что
, и тогда возможно, что 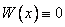 на
на  .
.
Пример 5. Легко проверить, что функции

линейно независимы на 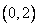 и для них
и для них 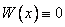 на
на 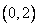 .
.
Это связано с тем, что функция 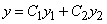 является общим решением уравнения
является общим решением уравнения
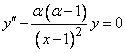 ,
,
где 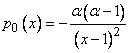 разрывна в точке
разрывна в точке 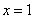 . Для этого уравнения теорема существования и единственности не имеет места (в окрестности точки
. Для этого уравнения теорема существования и единственности не имеет места (в окрестности точки 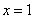 ). Не только функция
). Не только функция 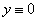 , но и функция
, но и функция 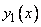 является решением дифференциального уравнения, удовлетворяющим условиям
является решением дифференциального уравнения, удовлетворяющим условиям 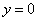 и
и 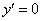 при
при 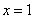 .
.
Структура общего решения.
Яндекс.Директ Все объявления  Решение уравнений онлайн! Калькулятор ЛовиОтвет – решение уравнений одним кликом! Скачай бесплатно!loviotvet.ru Кто такой Иисус Как узнать, кто такой Иисус Христос на самом деле?godlovesrussia.com
Решение уравнений онлайн! Калькулятор ЛовиОтвет – решение уравнений одним кликом! Скачай бесплатно!loviotvet.ru Кто такой Иисус Как узнать, кто такой Иисус Христос на самом деле?godlovesrussia.com
Теорема 4. Если 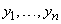 - линейно независимые на
- линейно независимые на  решения линейного однородного дифференциального уравнения
решения линейного однородного дифференциального уравнения 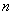 -го порядка
-го порядка 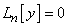 с непрерывными коэффициентами
с непрерывными коэффициентами 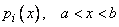 , то функция
, то функция
 , (9)
, (9)
где 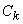 - произвольные постоянные, является общим решением уравнения
- произвольные постоянные, является общим решением уравнения 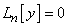 , т. е. сумма (9) при любых
, т. е. сумма (9) при любых 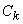 , есть решение этого уравнения и, обратно, всякое решение этого уравнения представимо в виде суммы (9) при соответствующих значениях
, есть решение этого уравнения и, обратно, всякое решение этого уравнения представимо в виде суммы (9) при соответствующих значениях 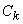 .
.
Доказательство. Мы уже знаем, что сумма (9) при любых 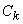 есть решение уравнения
есть решение уравнения 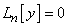 . Пусть, обратно,
. Пусть, обратно, 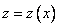 есть произвольное решение этого уравнения. Положим
есть произвольное решение этого уравнения. Положим
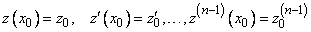 . (10)
. (10)
Для полученных чисел 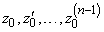 составим линейную систему уравнений относительно неизвестных чисел
составим линейную систему уравнений относительно неизвестных чисел 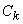 :
:
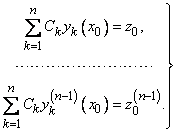 (11)
(11)
Определитель системы (11) 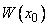 не равен нулю, так как функции
не равен нулю, так как функции 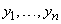 — линейно независимые на
— линейно независимые на  решения уравнения
решения уравнения 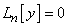 . Поэтому существует единственная система чисел
. Поэтому существует единственная система чисел 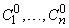 , удовлетворяющих уравнениям (11). Подставляя их в (9), получим решение нашего уравнения в виде
, удовлетворяющих уравнениям (11). Подставляя их в (9), получим решение нашего уравнения в виде
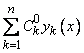 ,
,
удовлетворяющее тем же начальным условиям (10), которым удовлетворяет 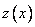 . Но тогда на основании теоремы существования и единственности имеет место равенство
. Но тогда на основании теоремы существования и единственности имеет место равенство 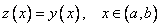 . Теорема доказана.
. Теорема доказана.
Таким образом, чтобы найти общее решение однородного уравнения 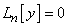 , достаточно найти какие-нибудь
, достаточно найти какие-нибудь 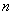 линейно независимых решений этого уравнения, и тогда общее решение будет их линейной комбинацией (9). Напомним, что любую совокупность из
линейно независимых решений этого уравнения, и тогда общее решение будет их линейной комбинацией (9). Напомним, что любую совокупность из 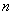 линейно независимых частных решений уравнения
линейно независимых частных решений уравнения 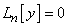 мы условились называть фундаментальной системой решений этого уравнения.
мы условились называть фундаментальной системой решений этого уравнения.
Возникает вопрос, всегда ли существует фундаментальная система (3) с непрерывными коэффициентами? Покажем, что существует.
Зададим 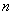 векторов
векторов

Каждому из этих векторов приведем в соответствие решение 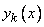 уравнения (3). Именно, пусть
уравнения (3). Именно, пусть 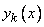 есть решение, удовлетворяющее следующим начальным условиям:
есть решение, удовлетворяющее следующим начальным условиям:

Определитель Вронского 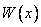 для этой системы решений при
для этой системы решений при 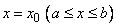 , очевидно, есть определитель матрицы, составленной из векторов
, очевидно, есть определитель матрицы, составленной из векторов 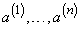 . Он равен 1:
. Он равен 1:
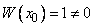 .
.
Но тогда система решений 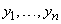 линейно независима, потому что для зависимой системы определитель Вронского был бы тождественно равен нулю.
линейно независима, потому что для зависимой системы определитель Вронского был бы тождественно равен нулю.
20.Теорема о структуре общего решения линейного однородного дифференциального уравнения


Ответ на вопрос 21-23
| 4. Линейные однородные уравнения с постоянными коэффициентами |
Рассмотрим дифференциальное уравнение 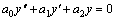 , (8) где , (8) где 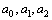 – вещественные постоянные. Для нахождения общего решения уравнения (8) поступаем так. Составляем характеристическое уравнение для уравнения (8): – вещественные постоянные. Для нахождения общего решения уравнения (8) поступаем так. Составляем характеристическое уравнение для уравнения (8): 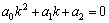 (9) Пусть (9) Пусть 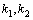 - корни уравнения (9), причем среди них могут быть и кратные. Возможны следующие случаи: а) - корни уравнения (9), причем среди них могут быть и кратные. Возможны следующие случаи: а) 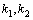 - вещественные и различные. Общим решением однородного уравнения будет - вещественные и различные. Общим решением однородного уравнения будет 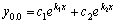 ; б) корни характеристического уравнения вещественные, но среди них есть кратные, т.е. ; б) корни характеристического уравнения вещественные, но среди них есть кратные, т.е. 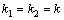 , тогда общее решение будет , тогда общее решение будет 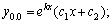 в) если корни характеристического уравнения комплексные (k=a±bi), то общее решение имеет вид в) если корни характеристического уравнения комплексные (k=a±bi), то общее решение имеет вид 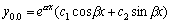 . Пример 8. Решить уравнение, y"-4y¢+3y=0, y(0)=6, y¢(0)=10. Решение. Составим характеристическое уравнение . Пример 8. Решить уравнение, y"-4y¢+3y=0, y(0)=6, y¢(0)=10. Решение. Составим характеристическое уравнение 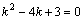 . Решим . Решим 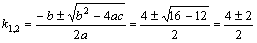 . . 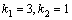 - корни различны. Значит, - корни различны. Значит, 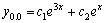 . Используя начальные условия, определим . Используя начальные условия, определим 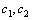 , так как y(0)=6 и y¢(0)=10, то , так как y(0)=6 и y¢(0)=10, то 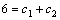 и и 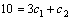 . Решаем систему: . Решаем систему: 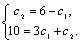 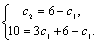 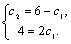 Получаем Получаем 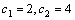 , тогда частное решение имеет вид: , тогда частное решение имеет вид: 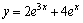 . Пример 9. Решить уравнение y"+9y=0. Решение. Составим характеристическое уравнение . Пример 9. Решить уравнение y"+9y=0. Решение. Составим характеристическое уравнение 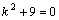 . Решаем его: . Решаем его: 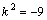 , отсюда , отсюда 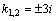 . Корни характеристического уравнения комплексные: α=0, β=3. Тогда общее решение имеет вид . Корни характеристического уравнения комплексные: α=0, β=3. Тогда общее решение имеет вид 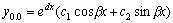 или или 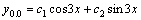 . . |
24.Линейные неоднородные уравнения. Принцип суперпозиции. Теорема о структуре общего решения линейного неоднородного уравнения
Рассмотрим линейное дифференциальное уравнение n –го порядка
y(n) + an-1(x)y(n - 1) + ... + a1(x)y' + a0(x)y = f(x).
с непрерывными коэффициентами an-1(x), an-2(x), ..., a1(x), a0(x) и непрерывной правой частью f(x).
Принцип суперпозиции основан на следующих свойствах решений линейных дифференциальных уравнений.
1. Если y1(x) и y2(x)— два решения линейного однородного дифференциального уравнения
y(n) + an-1(x)y(n - 1) + ... + a1(x)y' + a0(x)y = 0
то любая их линейная комбинация y(x) = C1y1(x) + C2y2(x) является решением этого однородного уравнения.
2. Если y1(x) и y2(x) — два решения линейного неоднородного уравнения L(y) = f(x) , то их разность y(x) = y1(x) − y2 (x) является решением однородного уравнения L(y) = 0 .
3. Любое решение неоднородного линейного уравнения L(y) = f(x) есть сумма любого фиксированного (частного) решения неоднородного уравнения и некоторого решения однородного уравнения.
4. Если y1(x) и y2(x) — решения линейных неоднородных уравнений L(y) = f1

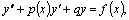
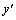 и
и 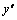 . Коэффициенты
. Коэффициенты 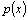 и
и 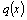 и правая часть
и правая часть 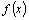 этого уравнения непрерывны.
этого уравнения непрерывны.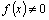 , то уравнение называют линейным неоднородным. Если же
, то уравнение называют линейным неоднородным. Если же 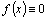 , то уравнение имеет вид
, то уравнение имеет вид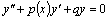
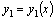 и
и 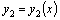 –какие–либо частные решения уравнения (9), то есть не содержат произвольных постоянных.
–какие–либо частные решения уравнения (9), то есть не содержат произвольных постоянных.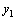 и
и 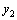 –два частных решения линейного однородного уравнения второго порядка, то
–два частных решения линейного однородного уравнения второго порядка, то 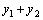 так же является решением этого уравнения.
так же является решением этого уравнения.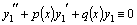 и
и 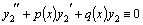
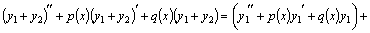
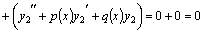 в силу (10). Значит,
в силу (10). Значит, 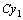 также является решением этого уравнения.
также является решением этого уравнения.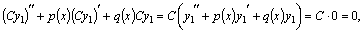 то есть
то есть 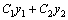 так же является его решением в силу теорем (1) и (2).
так же является его решением в силу теорем (1) и (2).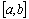 ), если можно подобрать такие числа
), если можно подобрать такие числа 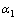 и
и 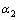 , не равные одновременно нулю, что линейная комбинация этих решений тождественно равна нулю на
, не равные одновременно нулю, что линейная комбинация этих решений тождественно равна нулю на 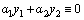 .
.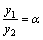 (или наоборот
(или наоборот 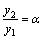 ).
).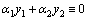 , где по меньшей мере одна постоянная
, где по меньшей мере одна постоянная 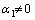 . Тогда
. Тогда 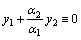 ,
, 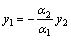 ,
, 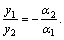 Обозначая
Обозначая 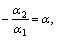 получим
получим 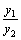 –постоянно.
–постоянно.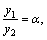 то
то 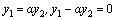 . Здесь коэффициент при
. Здесь коэффициент при 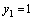 , то есть отличен от нуля, что по определению означает, что
, то есть отличен от нуля, что по определению означает, что 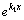 и
и 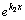 при
при 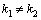 –линейно независимы, так как
–линейно независимы, так как 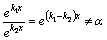 , так как
, так как 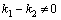 . А вот функции 5x и x–линейно зависимы, так как их отношение
. А вот функции 5x и x–линейно зависимы, так как их отношение 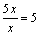 .
.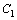 и
и 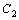 –произвольные постоянные, является общим решением этого уравнения.
–произвольные постоянные, является общим решением этого уравнения.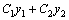 –общее решение, так как это решение содержит две произвольные постоянные, которые не могут быть сведены к одной.
–общее решение, так как это решение содержит две произвольные постоянные, которые не могут быть сведены к одной.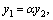
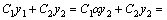
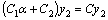 , где
, где 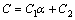 является постоянной.
является постоянной. 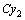 не может быть общим решением дифференциального уравнения второго порядка, так как зависит лишь от одной постоянной.
не может быть общим решением дифференциального уравнения второго порядка, так как зависит лишь от одной постоянной.