Предел последовательности и функции, определение и свойства предела; неопределённости, замечательные пределы.
Предел последовательности и функции, определение и свойства предела; неопределённости, замечательные пределы.
Предел последовательности и функции. Определение. Число А называется пределом функции f(x)в точке x = 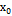 , если для любого числа e>0 существует число б>0 такое, что для всех х?Х , х ≠
, если для любого числа e>0 существует число б>0 такое, что для всех х?Х , х ≠ 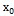 , удовлетворяющих неравенству
, удовлетворяющих неравенству 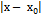 < б , выполняется неравенство
< б , выполняется неравенство 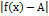 <e. Постоянное число а называется пределом последовательности {x n }, если для любого сколь угодно малого положительного числа e существует номер N, что все значения x n , у которых n>N, удовлетворяют неравенству
<e. Постоянное число а называется пределом последовательности {x n }, если для любого сколь угодно малого положительного числа e существует номер N, что все значения x n , у которых n>N, удовлетворяют неравенству 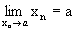 . Последовательность, имеющая предел, называется сходящейся, в противном случае - расходящейся.
. Последовательность, имеющая предел, называется сходящейся, в противном случае - расходящейся.
Бесконечно малые и бесконечно большие. Если функция f(x) при x → a имеет предел, равный А, это записывается в виде 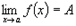 . В том случае, если последовательность {f(
. В том случае, если последовательность {f( 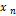 )} неограниченно возрастает (или убывает) при любом способе приближения x к своему пределу а, то будем говорить, что функция f(x) имеет бесконечный предел, и записывать это в виде:
)} неограниченно возрастает (или убывает) при любом способе приближения x к своему пределу а, то будем говорить, что функция f(x) имеет бесконечный предел, и записывать это в виде:  . Переменная величина (т.е. последовательность или функция), имеющая своим пределом нуль, называется бесконечно малой величиной. Переменная величина, имеющая бесконечный предел, называется бесконечно большой величиной.
. Переменная величина (т.е. последовательность или функция), имеющая своим пределом нуль, называется бесконечно малой величиной. Переменная величина, имеющая бесконечный предел, называется бесконечно большой величиной.
Свойства пределов функции. 1) Предел постоянной величины. Предел постоянной величины равен самой постоянной величине: 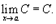 2) Предел суммы. Предел суммы двух функций равен сумме пределов этих функций:
2) Предел суммы. Предел суммы двух функций равен сумме пределов этих функций: 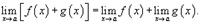 Аналогично предел разности двух функций равен разности пределов этих функций.
Аналогично предел разности двух функций равен разности пределов этих функций.
Расширенное свойство предела суммы: Предел суммы нескольких функций равен сумме пределов этих функций: 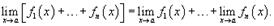 Аналогично предел разности нескольких функций равен разности пределов этих функций.3) Предел произведения функции на постоянную величину. Постоянный коэффициэнт можно выносить за знак предела:
Аналогично предел разности нескольких функций равен разности пределов этих функций.3) Предел произведения функции на постоянную величину. Постоянный коэффициэнт можно выносить за знак предела: 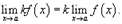 4) Предел произведения. Предел произведения двух функций равен произведению пределов этих функций:
4) Предел произведения. Предел произведения двух функций равен произведению пределов этих функций: 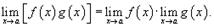 Расширенное свойство предела произведения. Предел произведения нескольких функций равен произведению пределов этих функций:
Расширенное свойство предела произведения. Предел произведения нескольких функций равен произведению пределов этих функций: 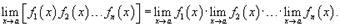 5) Предел частного. Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:
5) Предел частного. Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю: 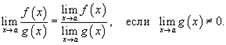
Замечательные пределы. 1) 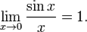 2)
2) 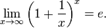
 Неопределенности.
Неопределенности.
Определенный интеграл: определение, свойства, формула Ньютона-Лейбница.
Определение.Определённым интегралом от функции 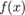 на отрезке
на отрезке 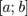 называется предел интегральных сумм при стремлении ранга разбиения к нулю
называется предел интегральных сумм при стремлении ранга разбиения к нулю  , если он существует независимо от разбиения R и выбора точек
, если он существует независимо от разбиения R и выбора точек 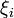 , т.е.
, т.е. 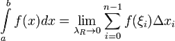
Свойства.Ниже предполагается, что f (x) и g (x) - непрерывные функции на замкнутом интервале [a, b]:
1) 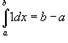 2)
2) 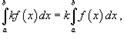 где k – константа; 3)
где k – константа; 3) 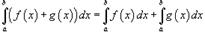 4)
4) 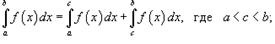 5) Если
5) Если 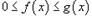 для всех
для всех 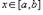 , то
, то 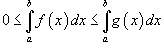 ; 6)
; 6) 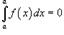 ; 7)
; 7) 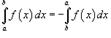 ; 8)Если
; 8)Если 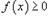 в интервале [a, b], то
в интервале [a, b], то 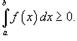 .
.
Формула Ньютона-Лейбница. Пусть функция f (x) непрерывна на замкнутом интервале [a, b]. Если F (x) - первообразная функции f (x) на [a, b], то 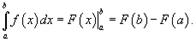
Предел последовательности и функции, определение и свойства предела; неопределённости, замечательные пределы.
Предел последовательности и функции. Определение. Число А называется пределом функции f(x)в точке x = 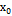 , если для любого числа e>0 существует число б>0 такое, что для всех х?Х , х ≠
, если для любого числа e>0 существует число б>0 такое, что для всех х?Х , х ≠ 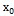 , удовлетворяющих неравенству
, удовлетворяющих неравенству 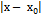 < б , выполняется неравенство
< б , выполняется неравенство 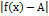 <e. Постоянное число а называется пределом последовательности {x n }, если для любого сколь угодно малого положительного числа e существует номер N, что все значения x n , у которых n>N, удовлетворяют неравенству
<e. Постоянное число а называется пределом последовательности {x n }, если для любого сколь угодно малого положительного числа e существует номер N, что все значения x n , у которых n>N, удовлетворяют неравенству 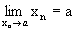 . Последовательность, имеющая предел, называется сходящейся, в противном случае - расходящейся.
. Последовательность, имеющая предел, называется сходящейся, в противном случае - расходящейся.
Бесконечно малые и бесконечно большие. Если функция f(x) при x → a имеет предел, равный А, это записывается в виде 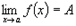 . В том случае, если последовательность {f(
. В том случае, если последовательность {f( 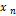 )} неограниченно возрастает (или убывает) при любом способе приближения x к своему пределу а, то будем говорить, что функция f(x) имеет бесконечный предел, и записывать это в виде:
)} неограниченно возрастает (или убывает) при любом способе приближения x к своему пределу а, то будем говорить, что функция f(x) имеет бесконечный предел, и записывать это в виде:  . Переменная величина (т.е. последовательность или функция), имеющая своим пределом нуль, называется бесконечно малой величиной. Переменная величина, имеющая бесконечный предел, называется бесконечно большой величиной.
. Переменная величина (т.е. последовательность или функция), имеющая своим пределом нуль, называется бесконечно малой величиной. Переменная величина, имеющая бесконечный предел, называется бесконечно большой величиной.
Свойства пределов функции. 1) Предел постоянной величины. Предел постоянной величины равен самой постоянной величине: 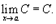 2) Предел суммы. Предел суммы двух функций равен сумме пределов этих функций:
2) Предел суммы. Предел суммы двух функций равен сумме пределов этих функций: 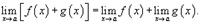 Аналогично предел разности двух функций равен разности пределов этих функций.
Аналогично предел разности двух функций равен разности пределов этих функций.
Расширенное свойство предела суммы: Предел суммы нескольких функций равен сумме пределов этих функций: 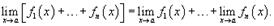 Аналогично предел разности нескольких функций равен разности пределов этих функций.3) Предел произведения функции на постоянную величину. Постоянный коэффициэнт можно выносить за знак предела:
Аналогично предел разности нескольких функций равен разности пределов этих функций.3) Предел произведения функции на постоянную величину. Постоянный коэффициэнт можно выносить за знак предела: 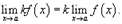 4) Предел произведения. Предел произведения двух функций равен произведению пределов этих функций:
4) Предел произведения. Предел произведения двух функций равен произведению пределов этих функций: 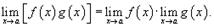 Расширенное свойство предела произведения. Предел произведения нескольких функций равен произведению пределов этих функций:
Расширенное свойство предела произведения. Предел произведения нескольких функций равен произведению пределов этих функций: 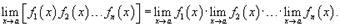 5) Предел частного. Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:
5) Предел частного. Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю: 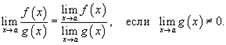
Замечательные пределы. 1) 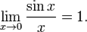 2)
2) 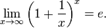
 Неопределенности.
Неопределенности.
