Выпуклость, вогнутость и точки перегиба. Их связь со второй производной.

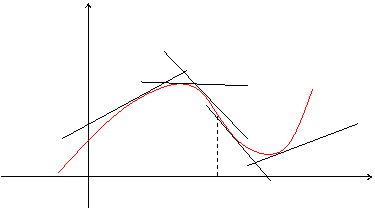Кривая обращена выпуклостью вверх на интервале (а, b), если все ее точки лежат ниже любой ее касательной на этом интервале. Кривая, обращенная выпуклостью вверх, называется выпуклой, а кривая, обращенная выпуклостью вниз – называется вогнутой. у

Теорема 1. Если во всех точках интервала (a, b) вторая производная функции f(x) отрицательна, то кривая y = f(x) обращена выпуклостью вверх (выпукла).

Доказательство. Пусть х₀ Î (a, b). Проведем касательную к кривой в этой точке.

Уравнение кривой: y = f(x);

Уравнение касательной: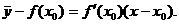

Следует доказать, что .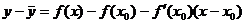

По теореме Лагранжа для f(x) – f(x₀): 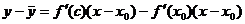, x₀ < c < x.

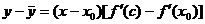
По теореме Лагранжа для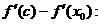

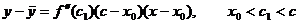
Пусть х > x₀ тогда x₀ < c₁ < c < x. Т.к. x – x₀ > 0 и c – x₀ > 0, и кроме того по условию

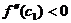, следовательно, .

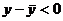Пусть x < x₀ тогда x < c < c₁ < x₀ и x – x₀ < 0, c – x₀ < 0, т.к. по условию 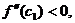то

.

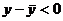Аналогично доказывается, что если f¢¢(x) > 0 на интервале (a, b), то кривая y=f(x) вогнута на интервале (a, b).

Теорема доказана.

Точка, отделяющая выпуклую часть кривой от вогнутой, называется точкой перегиба.

Очевидно, что в точке перегиба касательная пересекает кривую.

Теорема 2. Пусть кривая определяется уравнением y = f(x). Если вторая производная f¢¢(a) = 0 или f¢¢(a) не существует и при переходе через точку х = а f¢¢(x) меняет знак, то точка кривой с абсциссой х = а является точкой перегиба.

Доказательство. 1) Пусть f¢¢(x) < 0 при х < a и f¢¢(x) > 0 при x > a. Тогда при

x < a кривая выпукла, а при x > a кривая вогнута, т.е. точка х = а – точка перегиба.

1) Пусть f¢¢(x) > 0 при x < b и f¢¢(x) < 0 при x < b. Тогда при x < b кривая обращена выпуклостью вниз, а при x > b – выпуклостью вверх. Тогда x = b – точка перегиба.

2) Пусть f¢¢(x) > 0 при x < b и f¢¢(x) < 0 при x < b. Тогда при x < b кривая обращена выпуклостью вниз, а при x > b – выпуклостью вверх. Тогда x = b – точка перегиба.

Теорема доказана.

3. Вычислить .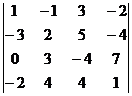

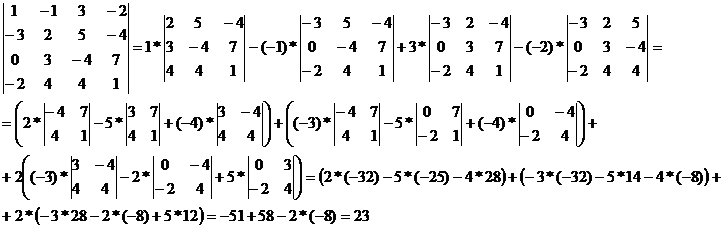
4. Вычислить .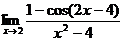

БИЛЕТ № 11.

1. Преобразование координат вектора при переходе к новому базису.

Пусть в 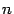-мерном линейном пространстве 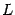выбран базис 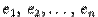, и другой, новый, базис 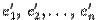. Возьмем произвольный вектор 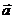из пространства 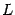. Его координатный столбец в старом базисе обозначим 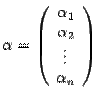, а в новом -- .

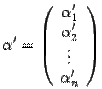Запишем разложения новых базисных векторов по старому базису:

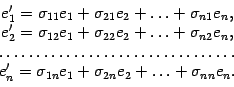
Составим матрицу, столбцами которой служат координатные столбцы векторов нового базиса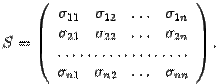

Эта матрица называется матрицей перехода от старого базиса к новому.

Координатные столбцы в старом базисе и в новом базисе связаны формулой 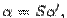где справа стоит произведение матрицы перехода 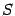на матрицу-столбец.

Доказательство. Так как 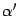- координатный столбец вектора 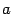в новом базисе, то 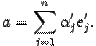. Заменив векторы 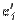их разложениями по старому базису, получим: .

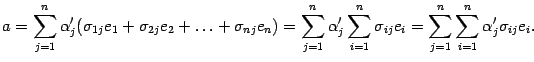Изменим порядок суммирования 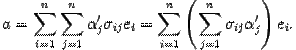Здесь мы получили разложение вектора 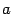по старому базису, причем координата вектора с номером 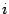равна 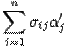. Элемент с номером 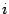столбца 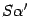будет иметь такой же вид. Следовательно, формула доказана.